User:Tomruen/Stellations of 16-cell

In 4-dimensional geometry, a stellation of a 16-cell is a 4-polytope constructed as volumes between hyperplane of the facets of a regular 16-cell.

Vertices

There are 4 sets of vertices as intersections of 4 hyperplanes:

Set	Typical member	Vertices	Distance from center	Convex polytope	Graph
1	(2,0,0,0)	8	2	{3,3,4}
2	(1,1,1,1)	16	2	{4,3,3}
3	(2,2,2,0)	32	2√3	r{4,3,3}
4	(4,2,2,2)	64	2√7	variation of t0,3{4,3,3}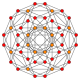

1-regions

These 4 sets define 7 1-regions (line segments):

Set	1 1	1 2	1 3	1 4	2 3	3 3	3 4
Length	2√2	2	2√2	4	2	2√2	2√2

2-regions

The 4 sets define 8 types of 2-regions (triangles|

Set	1 1 1	1 1 2	1 1 3	1 2 3	1 3 3	1 3 4	2 3 4	3 3 4
Type	Equilateral	Isosceles right	Equilateral	Isosceles right	Equilateral	Isosceles right	Isosceles right	Equilateral

3-regions

The 4 sets define 7 types of 3-regions (polyhedra):

Type	Description	Types of faces	Number
1 1 1 1	Regular tetrahedron	1 1 1	4
1 1 1 2	Tetrahedron	1 1 1	1
		1 1 2	3
1 1 2 3	Tetrahedron	1 1 2	1
		1 1 3	1
		1 2 3	2
1 1 3 3	Regular tetrahedron	1 1 3	2
		1 3 3	2
1 2 3 3	Tetrahedron	1 2 3	2
		1 3 3	1
		2 3 3	1
2 3 3 3 4	Triangular dipyramid	2 3 3	3
		3 3 4	3
1 3 3 4	Tetrahedron	1 3 3	1
		1 3 4	2
		3 3 4	1

layers

There are 5 layers (polychora):

Layer	Component	Structure	Number of components
a	16-cell	1 1 1 1	1
b	Simplex	1 1 1 1 1 1 1 2	16
c	Simplex	1 1 2 3	32
d	Simplex	1 1 2 3 1 1 3 3 1 2 3 3	96
e		1 2 3 3 2 3 3 3 4 1 3 3 4	64

Stellations

There are 6 stellated forms:

Name	Composition	Description
A	a	8 vertices of 16-cell
B	a∪b	Compound of 2 tesseracts Partially regular [2γ4]β4
C	a∪b∪c	24 vertices of 24-cell
D	a∪b∪c∪d
e	e
De	a∪b∪c∪d∪e

References

• The Stellated Forms of the Sixteen-Cell B. L. Chilton The American Mathematical Monthly Vol. 74, No. 4 (Apr., 1967), pp. 372-378