User:Tomruen/Semioperators
Coxeter operators
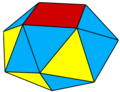
[edit]Coxeter/Johnson operators are sometimes useful to mix with Conway operators. For clarity in Conway notation these operations are given uppercase symbolic letter. Coxeter's t-notation defines active rings as indices a Coxeter-Dynkin diagram. So here a capital T with indices 0,1,2 define the uniform operators from a regular seed. The zero index cab ne see to represent vertices, 1 represents edges, and 2 represents faces. With T = T0,1 is an ordinary truncation, and R = T1 is a full truncation, or rectify, the same as Conway's ambo operator. For example, r{4,3} or t1{4,3} is Coxeter's name for a cuboctahedron, a rectified cube is RC, the same as Conway's ambo cube, aC.
| Operator | Example | Name | Alternate construction |
vertices | edges | faces | Description |
|---|---|---|---|---|---|---|---|
| T0 |  , t0{4,3} , t0{4,3} |
"Seed" | v | e | f | Seed form | |
| R = T1 | 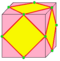 , t1{4,3} , t1{4,3} |
rectify | a | e | 2e | f+v | same as ambo, new vertices are added mid-edges, new faces centered on original vertices. Vertices are all valence 4. |
| T2 |  , t2{4,3} , t2{4,3} |
dual birectify |
d | f | e | v | dual of the seed polyhedron - each vertex creates a new face |
| T = T0,1 |  , t0,1{4,3} , t0,1{4,3} |
truncate | t | 2e | 3e | v+f | truncate all vertices. |
| T1,2 |  , t1,2{4,3} , t1,2{4,3} |
bitruncate | z = td | 2e | 3e | v+f | same as zip |
| RR = T0,2 | 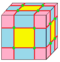 , t0,2{4,3} , t0,2{4,3} |
cantellate | aa=e | 2e | 4e | v+e+f | same as expand |
| TR = T0,1,2 | 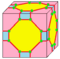 , t0,1,2{4,3} , t0,1,2{4,3} |
cantitruncate | ta | 4e | 6e | v+e+f | same as bevel |
Semioperators
[edit]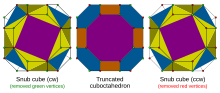
.

Coxeter's semi or demi operator, H for Half, reduces faces into half as many sides, and quadrilateral faces into digons, with two coinciding edges, which may or may not be replaced by a single edge. For example, a half cube, h{4,3}, also called a demicube, is HC, representing one of two tetrahedra. Ho reduces an ortho to ambo/Rectify.
Other semi-operators can be defined using the H operator. Conway calls Coxeter's Snub operation S, a semi-snub, defined as Ht. Conway's snub operator s is defined as SR. For example, SRC is a snub cube, sr{4,3}. Coxeter's snub octahedron, s{3,4} can be defined as SO, a pyritohedral symmetry construction of the regular icosahedron. It also is consistent with the Johnson solid snub square antiprism as SA4.
A semi-gyro operator, G, is defined as here dHt. This allows Conway's gyro g to be defined as GR. For example, GRC is a gyro-cube, gC or a pentagonal icositetrahedron. And GO defines a pyritohedron with pyritohedral symmetry, while gT, a gyro tetrahedron defines the same topological polyhedron with tetrahedral symmetry.
Both of these operators, S and G, require an even-valence seed polyhedra. In all of these semi-operations, there are two choices of alternated vertices within the half operator. These two construction are not topologically identical in the general case. For example, HjC ambiguously defines either a cube or octahedron, depending on which set of vertices are taken.
Other operators only apply to polyhedra with all even-sided faces. The simplest is the semi-join operator, as the conjugate operator of half, dHd.
A semi-ortho operator, F, is a conjugate operator to semi-snub. It adds a vertex in the center of the faces, and bisects all edges, but only connects new edges from each center to half of the edges, creating new hexagonal faces. Original square faces do not require the central vertex and need only a single edge across the face, creating pairs of pentagons. For example, a dodecahedron, tetartoid, can be constructed as FC.
A semi-expand operator, E, is defined as Htd or Hz. This creates triangular faces. For example, EC created a pyritohedral symmetry construction of a regular pseudoicosahedron.
| Operator | Example (Cube seed) |
Name | Alternate construction |
vertices | edges | faces | Description |
|---|---|---|---|---|---|---|---|
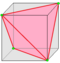
| H = H1 H2 |
  |
semi-ambo Half 1 and 2 |
v/2 | e-f4 | f-f4+v/2 | Alternation, remove half vertices. Quadrilateral faces (f4) are reduced to single edges. | |
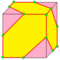
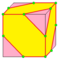
| I = I1 I2 |
  |
semi-truncate 1 and 2 |
v/2+e | 2e | f+v/2 | Truncate alternate vertices | |
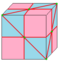 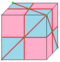 |
semi-needle 1 and 2 |
dI | v/2+f | 2e | e+v/2 | Needle at alternate vertices | |
| F = F1 F2 |
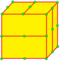 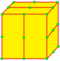 |
semi-ortho Flex 1 and 2 |
dHtd = dHz dSd |
v+e+f-f4 | 3e-f4 | e | Dual of semi-expand: This creates new vertices in edge and face centers. 2n-gons are divided into n hexagons. Quadrilateral faces (f4) won't have center vertices, so 2 pentagonal faces are created. |
| E = E1 E2 |
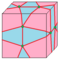  |
semi-expand Eco 1 and 2 |
Htd = Hz dF = Sd dGd |
e | 3e-f4 | v+e+f-f4 | Dual of semi-ortho: This create new triangular faces. Original faces will be replaced by half as many side polygons, with quadrilaterals (f4) reduced to single edges. |
| U = U1 U2 |
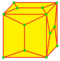 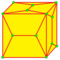 |
semi-lace CUp 1 and 2 |
v+e | 4e-f4 | 2e+f-f4 | Augment faces by cupolae. | |
| V = V1 V2 |
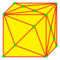  |
semi-lace Anticup 3 and 4 |
v+e | 5e-f4 | 3e+f-f4 | Augment faces by anticupolae | |
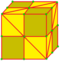 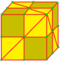 |
semi-medial 1 and 2 |
XdH = XJd | v+e+f | 5e | 3e | Diagonal alternate medial | |
  |
semi-medial 3 and 4 |
v+e+f | 5e | 3e | Middle alternate medial | ||
 |
semi-bevel 1 and 2 |
dXdH = dXJd | 3e | 5e | v+e+f | Diagonal alternate bevel | |
 |
semi-bevel 3 and 4 |
3e | 5e | v+e+f | Middle alternate bevel |
| Operator | Example (Octahedron seed) |
Name | Alternate construction |
vertices | edges | faces | Description |
|---|---|---|---|---|---|---|---|
| J = J1 J2 |
  |
semi-join 1 and 2 |
dHd | v-v4+f/2 | e-v4 | f/2 | Conjugate of half, join operator on alternate faces. New vertices are created at valence-4 vertices can be removed. 4-valence vertices (v4) reduced to 2-valence vertices are replaced by a single edge. |
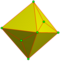 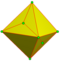 |
semi-kis 1 and 2 |
dId | v+f/2 | 2e | f/2+e | Kis alternate faces | |
 |
semi-zip 1 and 2 |
Id | f/2+e | 2e | v+f/2 | Zip alternate faces | |
| S = S1 S2 |
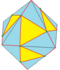 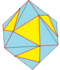 |
semi-snub 1 and 2 |
Ht dFd |
v-v4+e | 3e-v4 | f+e | Dual of semi-gyro: Coxeter snub operation, rotating the original faces, and with new triangular faces in the gaps. |
| G = G1 G2 |
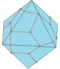 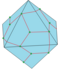 |
semi-gyro 1 and 2 |
dHt dS = Fd dEd |
f+e | 3e-v4 | v-v4+e | Dual of semi-snub: Create pentagonal and hexagonal faces along the original edges. |
  |
semi-medial 1 and 2 |
XdHd = XJ | 3e | 5e | v+e+f | Medial across alternate faces | |
 |
semi-bevel 1 and 2 |
dXdHd = dXJ | v+e+f | 5e | 3e | Bevel on alternate faces |
Examples
[edit]-
dHccC
-
dFtO
-
FtO
-
H1taC
-
H2taC
-
dH1taC
-
dH2taC
-
dHtmD
-
F1taD
-
F2taD
-
dF1taD
-
dF2taD
-
htA2
-
htA3=I
-
htA4
-
htA5
-
HdXQ
-
dHdXQ