User:Rodent21/sandbox
Dependence of Thermal and Hydrodynamic Boundary Layers on Prandtl Number
[edit]This article delves into the intricate relationship between thermal and hydrodynamic boundary layers in fluid mechanics, focusing on the influence of the Prandtl number. We explore the fundamental concepts of boundary layers, the significance of the Prandtl number, and the implications of its variation on heat transfer, fluid flow characteristics, and boundary layer separation.
1. Introduction
[edit]In fluid mechanics, boundary layers are pivotal in dictating the behaviour of fluids in motion near solid surfaces. When a fluid flows over a surface, the fluid particles in direct contact with the surface adhere to it due to viscous forces, resulting in a velocity gradient. This region of velocity variation is known as the hydrodynamic boundary layer. Similarly, a thermal boundary layer develops when there is a temperature difference between the fluid and the surface.
The Prandtl number (Pr), a dimensionless quantity, emerges as a key parameter in understanding the interplay between these two boundary layers. It is defined as the ratio of momentum diffusivity (ν) to thermal diffusivity (α):
Pr = ν / α
Where:
ν represents the kinematic viscosity, a measure of the fluid's resistance to shear flow.
α represents the thermal diffusivity, a measure of the fluid's ability to conduct heat.
The Prandtl number quantifies the relative effectiveness of momentum and heat transport within the fluid.
2. Hydrodynamic and Thermal Boundary Layers
[edit]2.1 Hydrodynamic Boundary Layer
[edit]Formation: As fluid flows over a surface, the fluid particles adjacent to the surface experience a retarding force due to friction. This frictional force, a manifestation of viscosity, causes the fluid velocity to decrease from the free stream velocity to zero at the surface. This region of velocity variation constitutes the hydrodynamic boundary layer.
Characteristics: The thickness of the hydrodynamic boundary layer increases along the flow direction as more fluid particles are affected by viscosity. The velocity profile within the boundary layer is typically characterised by a steep gradient near the surface, gradually transitioning to the free stream velocity.
Significance: The hydrodynamic boundary layer is crucial in determining skin friction drag, flow separation, and the overall flow pattern.
2.2 Thermal Boundary Layer
[edit]Formation: When there is a temperature difference between the fluid and the surface, heat transfer occurs, forming a thermal boundary layer. The fluid particles in contact with the surface assume the surface temperature, while those farther away retain the free stream temperature.
Characteristics: Like the hydrodynamic boundary layer, the thermal boundary layer grows thick along the flow direction. The temperature profile exhibits a steep gradient near the surface, gradually approaching the free stream temperature.
Significance: The thermal boundary layer governs the heat transfer rate between the fluid and the surface.
3. Influence of Prandtl Number
[edit]The Prandtl number significantly influences the relative thicknesses and development of the hydrodynamic and thermal boundary layers.
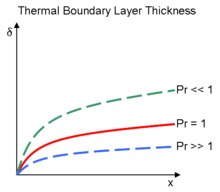
3.1 For Pr = 1
When Pr = 1, momentum and thermal diffusivities are equal, implying that momentum and heat are transported equally efficiently. Consequently, the hydrodynamic and thermal boundary layers grow at similar rates and have comparable thicknesses. This scenario is observed in gases like air.
3.2 For Pr > 1
When Pr > 1, momentum diffusivity dominates over thermal diffusivity; this indicates that momentum is transported more effectively than heat. As a result, the hydrodynamic boundary layer develops more rapidly and becomes thicker than the thermal boundary layer. This is typical of fluids like water, oils, and other liquids.
In forced convection, for incompressible flow over a flat plate, the ratio of the thermal to momentum boundary layer thickness over a flat plate is well approximated by
δt / δ ∝ Pr -1/3, Pr→∞,
Where δt = Thermal Boundary Layer
δ = Hydrodynamic Boundary Layer
3.3 For Pr < 1
When Pr < 1, thermal diffusivity exceeds momentum diffusivity, signifying that heat transport is more efficient than momentum transport. Consequently, the thermal boundary layer grows faster and thicker than the hydrodynamic boundary layer. Liquid metals, such as mercury, exhibit this behaviour.
In forced convection, for incompressible flow over a flat plate, the ratio of the thermal to momentum boundary layer thickness over a flat plate is well approximated by
δt / δ ∝ Pr -1/2, Pr→0,
Where δt = Thermal Boundary Layer
δ = Hydrodynamic Boundary Layer
4. Implications of Prandtl Number Variation
[edit]The variation in Prandtl number has profound implications on various aspects of fluid flow and heat transfer:
4.1 Heat Transfer Rate
The Prandtl number directly influences the heat transfer rate between the fluid and the surface.
Lower Pr values, indicating higher thermal diffusivity, lead to thicker thermal boundary layers and enhanced heat transfer rates.
Conversely, higher Pr values result in thinner thermal boundary layers and reduced heat transfer rates.
4.2 Boundary Layer Separation
The hydrodynamic boundary layer can separate from the surface in flows with adverse pressure gradients, leading to flow recirculation and increased drag.
The Prandtl number affects the location of separation. Higher Pr values, associated with thicker hydrodynamic boundary layers, promote earlier separation.
4.3 Fluid Flow Behavior
The Prandtl number affects the overall fluid flow behaviour, including velocity and temperature profiles, skin friction, and heat transfer coefficients.
These effects are particularly prominent in convective heat transfer processes, where the fluid motion plays a significant role in heat transport.
5. Conclusion
[edit]The Prandtl number is a fundamental fluid mechanics parameter governing the interplay between the hydrodynamic and thermal boundary layers. Its value dictates these layers' relative thicknesses and development, with profound implications for heat transfer, fluid flow characteristics, and boundary layer separation. Understanding the influence of the Prandtl number is crucial in various applications, from designing efficient heat exchangers to predicting aerodynamic performance.
References
[edit]- http://en.wiki.x.io/wiki/Prandtl_number
- Lienhard IV, John Henry; Lienhard V, John Henry (2017). A Heat Transfer Textbook (4th ed.). Cambridge, MA: Phlogiston Press.
- Chapter 6 - Forced convection, Heat Transfer Principles and Applications, https://doi.org/10.1016/B978-0-12-802296-2.00006-8
- White, F. M. (2006). Viscous Fluid Flow (3rd. ed.). New York: McGraw-Hill.
Article prepared by
[edit]- Naman Khetan (Roll no.-21135085), IIT BHU Varanasi
- Prathamesh Nikumbh (Roll no.-21135099), IIT BHU Varanasi
- Sayyam Jain (Roll no.-21135119), IIT BHU Varanasi
- Vineet Mathur (Roll no.-21135142), IIT BHU Varanasi
- Yogesh Sharma (Roll no.-21134031), IIT BHU Varanasi
