CALCULUS - SINGLE VARIABLE
[edit]x as infinite if it satisfies the conditions |x| > 1, |x| > 1 + 1, |x| > 1 + 1 + 1, ..., and infinitesimal if x ≠ 0 and a similar set of conditions holds for x and the reciprocals of the positive integers
Continuity and Limit
[edit]
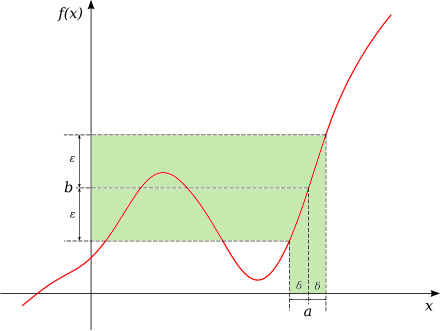
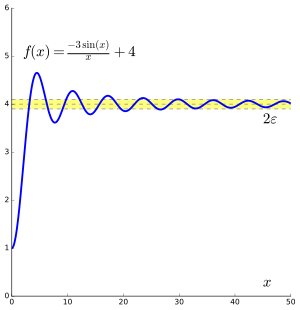
the function has a limit L at an input p, if f(x) gets closer and closer to L as x moves closer and closer to p
continuity of  by saying that an infinitesimal change in x necessarily produces an infinitesimal change in y
by saying that an infinitesimal change in x necessarily produces an infinitesimal change in y
A function f is said to be continuous at c if it is both defined at c and its value at c equals the limit of f as x approaches c:
 We have here assumed that c is a limit point of the domain of f.
We have here assumed that c is a limit point of the domain of f.


Differential Calculus
[edit]


For every positive real number  , there exists a positive real number
, there exists a positive real number  such that, for every
such that, for every  such that
such that  and
and  then
then  is defined, and
is defined, and

Leibniz Derivative Notation
[edit]The first derivative of  is denoted by
is denoted by  , read as "the derivative of
, read as "the derivative of  with respect to
with respect to  ".
".

 for the
for the  -th derivative of
-th derivative of 

Lagrange Derivative Notation
[edit]The first derivative is written as 
 for the
for the  th derivative of
th derivative of  .
.
Newton Derivative Notation
[edit]If  is a function of
is a function of  , then the first and second derivatives can be written as
, then the first and second derivatives can be written as  and
and 
Differential Operator Derivative Notation
[edit] and higher derivatives are written with a superscript, so the
and higher derivatives are written with a superscript, so the  -th derivative is
-th derivative is 
Let f(x) = x2 be the squaring function.

Leibniz Derivative Example
[edit]

Differentiation is linear
[edit] with respect to
with respect to  is:
is: 
- The constant factor rule

- The sum rule

- The difference rule


 , then
, then 


For the functions  and
and  , the derivative of the function
, the derivative of the function  with respect to
with respect to  is
is
 In Leibniz's notation this is written
In Leibniz's notation this is written

The derivative of the function  is
is

In Leibniz's notation, this is written as:
 often abridged to
often abridged to


If z = f(y) and y = g(x)
 and
and

If y = f(u) and u = g(x):








 or for short,
or for short,
 The derivative function is therefore:
The derivative function is therefore:

Chain Rule Higher Derivatives
[edit]Looks like the product rule.
f(u) and u = g(x):

The quotient rule is a consequence of the chain rule and the product rule. To see this, write the function f(x)/g(x) as the product f(x) · 1/g(x). First apply the product rule:


y = g(x) has an inverse function. Call its inverse function f so that we have x = f(y).


The derivative of  for any (nonvanishing) function f is:
for any (nonvanishing) function f is:
 wherever f is non-zero.
wherever f is non-zero.
In Leibniz's notation, this is written

Derivatives of exponential and logarithmic functions
[edit]





![{\displaystyle {\frac {d}{dx}}\left(f_{1}(x)^{f_{2}(x)^{\left(...\right)^{f_{n}(x)}}}\right)=\left[\sum \limits _{k=1}^{n}{\frac {\partial }{\partial x_{k}}}\left(f_{1}(x_{1})^{f_{2}(x_{2})^{\left(...\right)^{f_{n}(x_{n})}}}\right)\right]{\biggr \vert }_{x_{1}=x_{2}=...=x_{n}=x},{\text{ if }}f_{i<n}(x)>0{\text{ and }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e52623821c09e999ec428d4b2264ed2123e6c5c)

 wherever f is positive.
wherever f is positive.
Derivatives of Trigonometric Functions
[edit]

|

|

|

|

|

|

|

|

|

|

|

|
Derivatives of integrals
[edit]
where the functions  and
and  are both continuous in both
are both continuous in both  and
and  in some region of the
in some region of the  plane, including
plane, including 
 , and the functions
, and the functions  and
and  are both continuous and both have continuous derivatives for
are both continuous and both have continuous derivatives for  . Then for
. Then for  :
:

Integrals Rational Functions
[edit]




Integrals Exponential Functions
[edit]Integrals Trigonometric functions
[edit]







Power Rule Integration
[edit]


















































































![{\displaystyle {\frac {d}{dx}}\left(f_{1}(x)^{f_{2}(x)^{\left(...\right)^{f_{n}(x)}}}\right)=\left[\sum \limits _{k=1}^{n}{\frac {\partial }{\partial x_{k}}}\left(f_{1}(x_{1})^{f_{2}(x_{2})^{\left(...\right)^{f_{n}(x_{n})}}}\right)\right]{\biggr \vert }_{x_{1}=x_{2}=...=x_{n}=x},{\text{ if }}f_{i<n}(x)>0{\text{ and }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e52623821c09e999ec428d4b2264ed2123e6c5c)










































