This is a Wiki pedia user page . Wiki pedia ,mirror site . Be aware that the page may be outdated and that the user in whose space this page is located may have no personal affiliation with any site other than Wiki pedia http://en.wiki pedia.org/wi ki/User:Cavenba/Mathtastic
π
=
3.141592653589793238462643383279502884197169399375105820974944592307
{\displaystyle \pi =3.141592653589793238462643383279502884197169399375105820974944592307\,\!}
Trigonometric functions [ edit ]
sin
θ
=
opposite
hypotenuse
=
o
h
{\displaystyle \sin \theta ={\frac {\textrm {opposite}}{\textrm {hypotenuse}}}={\frac {o}{h}}}
cos
θ
=
adjacent
hypotenuse
=
a
h
{\displaystyle \cos \theta ={\frac {\textrm {adjacent}}{\textrm {hypotenuse}}}={\frac {a}{h}}}
tan
θ
=
opposite
adjacent
=
o
a
{\displaystyle \tan \theta ={\frac {\textrm {opposite}}{\textrm {adjacent}}}={\frac {o}{a}}}
Remember: SOHCAHTOA
{\displaystyle {\mbox{Remember: SOHCAHTOA}}\,\!}
sin
θ
=
o
/
h
or SOH
{\displaystyle \sin \theta =o/h{\mbox{ or SOH}}\,\!}
cos
θ
=
a
/
h
or CAH
{\displaystyle \cos \theta =a/h{\mbox{ or CAH}}\,\!}
tan
θ
=
o
/
a
or TOA
{\displaystyle \tan \theta =o/a{\mbox{ or TOA}}\,\!}
Trigonometric equations [ edit ]
If
sin
x
=
3
2
{\displaystyle {\mbox{If }}\sin x={\frac {\sqrt {3}}{2}}}
then
x
=
{
60
∘
+
360
∘
k
,
k
∈
I
120
∘
+
360
∘
k
,
k
∈
I
{\displaystyle {\mbox{then }}x={\begin{cases}60^{\circ }+360^{\circ }k,k\in \mathbb {I} \\120^{\circ }+360^{\circ }k,k\in \mathbb {I} \end{cases}}}
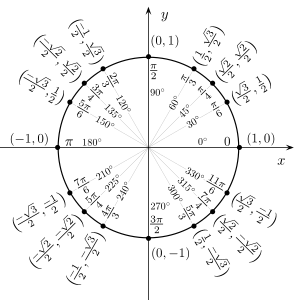
Trigonometric identities [ edit ] The unit circle can be very helpful 1.
csc
θ
=
1
sin
θ
{\displaystyle \csc \theta ={\frac {1}{\sin \theta }}}
sec
θ
=
1
cos
θ
{\displaystyle \sec \theta ={\frac {1}{\cos \theta }}}
cot
θ
=
1
tan
θ
{\displaystyle \cot \theta ={\frac {1}{\tan \theta }}}
4.
tan
θ
=
sin
θ
cos
θ
{\displaystyle \tan \theta ={\frac {\sin \theta }{\cos \theta }}}
cot
θ
=
cos
θ
sin
θ
{\displaystyle \cot \theta ={\frac {\cos \theta }{\sin \theta }}}
6.
sin
2
θ
+
cos
2
θ
=
1
{\displaystyle \sin ^{2}\theta +\cos ^{2}\theta =1\,\!}
tan
2
θ
+
1
=
sec
2
θ
{\displaystyle \tan ^{2}\theta +1=\sec ^{2}\theta \,\!}
1
+
cot
2
θ
=
csc
2
θ
{\displaystyle 1+\cot ^{2}\theta =\csc ^{2}\theta \,\!}
Prove.
sec
x
+
1
cot
x
=
1
+
sin
x
cos
x
{\displaystyle {\mbox{Prove. }}\sec x+{\frac {1}{\cot x}}={\frac {1+\sin x}{\cos x}}}
(
1
cos
x
)
+
(
sin
x
cos
x
)
=
1
+
sin
x
cos
x
{\displaystyle \left({\frac {1}{\cos x}}\right)+\left({\frac {\sin x}{\cos x}}\right)={\frac {1+\sin x}{\cos x}}}
1
+
sin
x
cos
x
=
1
+
sin
x
cos
x
{\displaystyle {\frac {1+\sin x}{\cos x}}={\frac {1+\sin x}{\cos x}}}
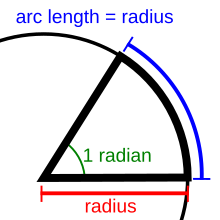
An angle of 1 radian subtends an arc equal in length to the radius of the circle . The radian is a unit of plane angle , equal to 180/π degrees , or about 57.296 degrees. It is the standard unit of angular measurement in all areas of mathematics beyond the elementary level.
Important equations [ edit ]
Arc Length
=
2
π
r
(
θ
360
∘
)
{\displaystyle {\mbox{Arc Length}}=2\pi r\left({\frac {\theta }{360^{\circ }}}\right)}
1
complete circle
=
360
∘
(
1
rad
57.296
∘
)
=
2
π
{\displaystyle 1{\mbox{ complete circle}}=360^{\circ }\left({\frac {1{\mbox{ rad}}}{57.296^{\circ }}}\right)=2\pi }
30
∘
(
π
180
∘
)
=
30
π
180
=
π
6
rad
{\displaystyle 30^{\circ }\left({\frac {\pi }{180^{\circ }}}\right)={\frac {30\pi }{180}}={\frac {\pi }{6}}{\mbox{ rad}}}
3
π
4
(
180
∘
π
)
=
135
∘
{\displaystyle {\frac {3\pi }{4}}\left({\frac {180^{\circ }}{\pi }}\right)=135^{\circ }}