Talk:Venn diagram/Archive 1
| This is an archive of past discussions about Venn diagram. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 |
Merge from euler diagram
I'm fairly sure these are one and the same, as discussed above. I think Euler diagram should redirect to here and a note made on name variation. There may be some content in Euler diagram worht keeping. --Salix alba (talk) 18:52, 18 January 2006 (UTC)
- It looks like Venn diagrams are subsets of Euler diagrams, not the other way around, so it'd have to be merged into Euler diagram, which would be a bad idea because Euler diagrams aren't as well-known. --AySz88^-^ 03:14, 19 January 2006 (UTC)
Yes there does seem to be some confusion. At [Stanford Encyclopedia of Philosophy] they mention Venn's Primary diagrams, which are what we are calling Venn diagrams. It would be good to make the destinction clear. I've a feeling some people do refer to Euler diagrams as Venn diagrams and we should make this clear. --Salix alba (talk) 17:17, 19 January 2006 (UTC)
Johnston Diagrams
The pictures given for these are all said to be Edwards-Venn diagrams on their respective pages, and the page on A. W. F. Edwards has the picture of the six-set one with the caption "Six-set Edwards-Venn diagram". Are they the same thing, or the wrong graphic? --Nucleusboy 23:50, 31 January 2006 (UTC) Check the article now especially the review of cogwheels, that should clarify your question. --Salix alba (talk) 03:00, 1 February 2006 (UTC)
Similar diagrams
I don't think the Euler, Johnstone etc. should be on the page as it stands, since they are not Venn diagrams - at most they should be wikilinked from a See Also section or similar. — SteveRwanda 12:49, 24 March 2006 (UTC)
Intersection or Union
I think there may be a mistake in the following sentence :
The combined area of sets A and B is called the union of sets A and B. The union, in this case, contains all things which either have two legs, fly's, or both.The overlaping circles implies that the union of the two sets is not empty - that, in fact, there are creatures that are in both of the orange and blue circles.
In set theory, the union of A and B is every element that belongs to A or that belongs to B, but the overlaping circles defines elements that belong to A and to B, that its intersection.
Isn't it ?
Zejames 21:06, 23 May 2006 (UTC)
Sven diagrams?
Some people erroneously call them Sven diagrams, this term appears to have originated in certain parts of Montreal. Surely this is a joke? Either way, I'm not sure it's much of an issue, as most people learn about them in math class from teachers who know the correct term, so I can't imagine it's a widespread error. That sentence ought to be deleted if it remains unsourced. OneVeryBadMan 15:05, 19 July 2006 (UTC)
All monkeys are primates.
This Venn diagram from The Fallacy Files is given to illustrate the proposition "All monkeys are primates", where S is the subject (Monkeys) and P is the predicate (Primates).
http://img219.imageshack.us/img219/6671/picture1be5.png
What I don't understand is why there is this high-lighted red area where S and P do not overlap? Doesn't this imply that there are monkeys which are not primates? Isn't this A-type proposition better represented with a Euler diagram, having S inside (as a subset of) P? Or does red represent emptiness?
What am I missing?
- In that case I think the the red indicates emptyness, i.e. the disallowed elements. Yes you could use an Euler diagram which indicates the concept better. The ven diagram is useful as it explicity shows whats not allowed. --Salix alba (talk) 17:06, 30 September 2006 (UTC)
Error ?
Shouldn't the sentence "Mosquitos have six legs, and fly, so the point for mosquitos would be in the part of the blue circle which does not overlap with the orange one." paragraph 2 read ". . . the part of the blue circle which overlaps with the orange one . . ." —Preceding unsigned comment added by 58.111.208.201 (talk) 10:47, 8 October 2007 (UTC)
- No. The area where the blue and orange circles overlap contains those living creatures that can fly and have two legs. Mosquitoes can fly but do not have two legs, so they are outside the orange circle. --Lambiam 13:56, 8 October 2007 (UTC)
Classroom use ?
Not sure about the appropriateness of this section, though I like the attempt to address a more general audience - I find this article a little too math text book-y. More importantly though: I've never seen the "three column" approach instead of overlapping circles (and I can't picture how it would work - how do you represnt a u b u c? Or more than three sets?). And the "compare and contrast two items" [my emphasis] piece doesn't make sense to me. Is there a citation for this? Is it common to a particular educational approach? Is it just the general new approach to teaching that I'm too old to remember :-) ? --SiobhanHansa 01:10, 16 August 2006 (UTC)
- I am not sure about the relevance of the Indian classrooms point, I could say that in New Zealand they teach them using powerpoint slides, but really what is the relevance. Nzv8fan 08:25, 3 June 2007 (UTC)
- I've gone ahead and removed that sentance. It wasn't relevent, and it was just akward. Kopophex (talk) 12:22, 7 January 2008 (UTC)
A cartesian variation on Edwards diagrams
Edwards-diagrams are nice but not easy to draw. This on can be drawn on a grid, (with gray code in one collumn). See: http://home.versateladsl.be/vt649464/VenGray5.pdf Feel free to use it. Perhaps it exists already somewhere, I don't know.--Bleuprint (talk) 05:27, 8 February 2008 (UTC)
Proposal to blend Venn diagram with Euler diagram
The following appears on and is cc'd from the Talk:Set theory page at subsection "Venn diagram":
(begin copy)
Isn't it a bit ridiculous that we have separate articles for Venn diagram and Euler diagram, anyway? Perhaps the two should be merged, under the more common name Venn diagram, or perhaps Venn and Euler diagrams. A merged article could define Euler diagrams, introduce Venn diagram as a synonym, and say that Venn's original definition was more restrictive and how. Hans Adler 23:34, 17 November 2009 (UTC)
- I'd keep them separate. (But I agree that some explanation of differences and usages would be appropriate ...). My sense of the (true) Venn diagram is that it is now a backwater of mainly historical importance, but it is an important one on the way to the development of the Karnaugh map which is still a seriously-useful tool. On the other hand the "Euler diagram" is still useful for teaching purposes -- a visualization aid for solving thought-problems (see my explanatory examples at Talk:Law of excluded middle). I'll now verify and demonstrate this assertion about (true) Venn diagrams:
- I pulled open one of my switching-theory books -- Hill and Peterson 1968, 1974 Introduction to Switching Theory and Logical Design, John Wiley & Sons NY, ISBN 0-71-39882-9. This is an engineer's book. In chapter "Boolean Algebra" they present sections 4.5ff "Set Theory as an Example of Boolean Algebra" and in it they present the (true) Venn diagram with shading and all. They actually use Venn diagrams to solve example switching-circuit problems, but end up with this statement:
- "For more than three variables, the bsic illustrative form of the Venn diagram is inadequate. Extensions are possible, however, the most convenient of which is the Karnaugh map, to be discussed in Chapter 6." (p. 64)
- In Chapter 6, section 6.4 "Karnaugh Map Representation of Boolean Functions" they begin with:
- "The Karnaugh map1 [1Karnaugh 1953] is one of the most powerful tools in the repertory of the logic designer. ... A Karnaugh map may be regarded either as a pictorial form of a truth table or as an extension of the Venn diagram." pp. 103-104
- And that is the end of the Venn diagram in this book of 596 pages. I consulted three more engineering texts. Two of them -- (i) McClusky 1965 Introduction to the Theory of Switching Circuits, McGraw-Hill Book Company, NY, no ISBN; and (ii) Wickes 1968 Logic Design with Integrated Circuits, John Wiley and Sons, Inc, NY, no ISBN -- present (true) Venn diagrams the same way as did Hill and Peterson, that is as a feature of Boolean algebra, and perhaps as Wicks calls them "Minimization Aids". As an engineer I never use Venn diagrams, I always use Karnaugh maps (and have 1000's if not 10,000's of times so far). But, to explain simple set-theoretic concepts to myself I do use "Euler diagrams" (both with and without a box around them, which until 2 days ago I thought were Venn diagrams).
- To sum up, I'd keep the articles split mainly because of their historical significance. Otherwise we could use similar reasoning to fold Euler diagram into Venn diagram and both into Karnaugh map and then Karnaugh map into Hypercube. I think alot of this fussing has to do with didactic and historical precision, which as a historian is something I am very sensitive to. Bill Wvbailey (talk) 15:52, 18 November 2009 (UTC)
Interestingly, there is a Wikipedia article on Karnaugh maps at http://en.wiki.x.io/wiki/Karnaugh_map The Stanford Encyclopedia of Philosophy does not have a stand alone article on Karnaugh maps but discusses them under some other headings. Dagme (talk) 18:40, 18 November 2009 (UTC)
"Isn't it a bit ridiculous that we have separate articles for Venn diagram and Euler diagram, anyway? Perhaps the two should be merged" Yes, this is a good point and a good suggestion. It is what was done in the Stanford Encyclopedia of Philosophy. Since Wikipedia has a feature that redirects searches, both "Venn Diagram" and "Euler Diagram" could be redirected to a single article. The historical development could also be addressed there. The name of the article could be "Euler and Venn Diagrams". It could also be "Set Theoretic Diagrams", but with the latter, the more advanced topics in the Stanford article should also be included. Since we are already having more than enough difficulty with Euler and Venn Diagrams, I suggest the former. Dagme (talk) 18:40, 18 November 2009 (UTC)
(end copy)
- RE blending the articles: I stand on my recommendation not to. I think that ultimately, as time goes on, a single article will have to be split into two because of its size. Per my quote from Venn at Talk:Set theory under "Venn diagrams" he encountered 34 references that used versions of Euler diagrams. And then he observes a few (for him more recent sources) that shade the diagrams. The fact is: with respect to Euler diagrams Venn is a legitimate 2nd source. My point being that there is a ton of information that hasn't been sifted through yet (because just now these volumes are becoming available because of googlebooks -- that's where you can find Venn, Jevons, etc etc).
- RE a more unified treatment of the evolution from Euler diagrams to Venn diagrams to Veitch charts to Karnaugh maps: A mystery ensues, there's a huge gap. I now have cc's of the two main papers that define the notion of "Karnaugh map" -- Veitch 1952 and Karnaugh 1953. Karnaugh references Veitch (3rd reference). Veitch references Claude Shannon 1938, and Shannon references the same Couturat 1914 that I referenced at Talk:Set theory under section "Venn diagrams". I also have Shannon's 1938 "A Symbolic Analysis of Relay and Switching Circuits" (and a non-printable cc of his 1940 Master's thesis, the same thing). Nowhere in any of these (I OCR'd them and did a word search) is the Venn diagram mentioned except in Couturat who expresses his lack of enthusiasm: "This diagrammatic method has, however, serious inconveniences as a method for solving logical problems." (p. 75).
- So where did the ideas of Veitch and Karnaugh come from?? Maybe someone knows of a secondary reference that can serve as a guide. I know that by 1921 Emil Post (cf Post's paper in van Heijenoort 1967:264ff) had firmed up the notion of "truth table". We also know that by the 1940's all sorts of authors were incorporating truth tables into their treatments, e.g. Reichenbach 1947 "Elements of Symbolic Logic" and Tarski 1941, 1946 "Introduction to Logic" both reprinted by Dover -- I see Post referenced in both but there is no Venn in either. And yet by the late 1950's some authors (e.g. Kemeney et. al. 1958) were using so-called "Venn diagrams" (sometimes Euler diagrams, sometimes Venn diagrams) in their texts to teach "set theory" with respect to "Relations between sets and statements". This "set-theory-versus-logical-analysis" dichotomy strikes me as odd and needs to be accounted for, if we are to "unify" the history. Bill Wvbailey (talk) 20:40, 18 November 2009 (UTC)
- If it needs any seconding I second the motion to kill the merger. Though related they are logically two topics under two names and neither would comprise a very short article.Dave (talk) 02:10, 26 December 2009 (UTC)
Validity
This article seems to neglect validity which is why venn diagrams were invented according to dictionaries. I am also searching for sources about what the border space around which a venn diagram is placed, represents in limitations. I expect it is the range of valid quantifiers for the all the complete sets in the domain of discourse.  Zulu Papa 5 ☆ (talk) 22:31, 6 November 2009 (UTC)
Zulu Papa 5 ☆ (talk) 22:31, 6 November 2009 (UTC)
- That sounds very impressive. I recommend we put nothing at all in at that level. It needs to be watered down for the good reader, who can't drink such a heady wine. That would be a good project for you, write a paragraph or two explaining all that in English. We don't dazzle with our technical brilliance, we explain things to people who need explanations. At least, that is how I see it. The technical journals do the dazzling, or the young professors looking for an educated wife at a party. Top quark, lower quark, validity, domain of discourse, quack, quack.Dave (talk) 02:19, 26 December 2009 (UTC)
Image:Venn diagram cmyk.svg
I think that the first image on the page - Venn diagram cmyk.svg - could be misleading to someone who hasn't heard of a Venn diagram. It makes it look like Venn diagrams are all about colour mixing. Colour mixing is just an application of Venn diagrams. The colours of a Venn diagram aren't usually so directly related to the meaning it is trying to get across. Perhaps this can be corrected by better text but I would suggest choosing a better image. Yaris678 (talk) 14:56, 17 March 2009 (UTC)
- Sorry yaris old boy but folks I would like to throw my weight in favor of the color diagram. It seems most illustrative at a glance. My only objection would be that color-blind persons cannot read it and there are a significant minority of them. However I have made my recommendation of what to do about it below.Dave (talk) 02:33, 26 December 2009 (UTC)
flaws in the method
Venn diagrams are certainly not the right way to show anything the nomenclature can be very very misleading. for example a and b have an intersection if you call it a intersection b then when i say "a" does it also include elements in a and a intersection b i would rather call a, b and a.b as 3 separate outcomes. —Preceding unsigned comment added by 192.18.192.21 (talk) 10:30, 19 November 2008 (UTC)
Take for example a Set S with A B and C as possible subsets in it so if you call A intersection B as A.B then A itself should be called S.A because A is itself an intersection with the original set S. and A intersection B should be called "a intersection b intersection notC intersection S".likewise if there is another D, then as per "venn's massive wisdom" which I never did comprehend, "A intersection B" is actually termed as "S intersection A intersection B not D". Is my understanding of his nomenclature incorrect?
- Yes. Well, allow us the luxury of abbreviation. For eaxample, on your own computer you do not list the entire address of a file. Most scripts allow a default directory and then plug in the full address without us having to clutter up our English with it. This article is and ought to be in English.Dave (talk) 02:41, 26 December 2009 (UTC)
Images at the top are misleading
Just looking at the top 3 pictures, one could be forgiven for thinking that we are talking about subtractive colours. Can we please have normal circles? Also what happened to the dots inside the circles representing elements of the sets? I can't believe there is no example of that in the article. These solid discs bring no added value and are actually misleading/confusing. Thanks. 83.67.217.254 (talk) 21:04, 1 March 2008 (UTC)
- Disagree. Quite a large amount of added value: clarity, simplicity, readability, ease of use. Too much detail would remove these and the complexity would not be worth the perplexity.Dave (talk) 02:46, 26 December 2009 (UTC)
Too technical tag
I removed the tag. the article has undergone considerable revision since the tag was removed. if you feel that the tag still belongs, feel free to put it back but please make some specific suggestions about what could be improved. thanks. Lunch 04:53, 24 September 2006 (UTC)
- I don't think it needs a tag. I like it.Dave (talk) 02:47, 26 December 2009 (UTC)
Changes
It appears that major changes to this article have been made in the last few months, constituting a dramatic improvement. I have not had time to look thoroughly through the article and to analyze the changes, but it appears that most of my earlier objections have been or are being addressed. So a big "Thanks" to the contributors who are working so hard to clear up the mess.
Here are a few additional suggestions. The reference to Cyndi Joyce Aguzar at the beginning of the "Overview" section should either be given a target or removed. The sentence in which that reference occurs could be improved by making it more like the very fist sentence in the introductory section --- definitional rather than incidentally descriptive in character. It is important to stress that ALL possible intersections are shown and that those which are empty are indicated by shading, in contrast to Euler Diagrams, which indicated empty intersections as absent regions. In connection with this, I mention again that I don't think it is possible to understand Venn Diagrams without first understanding Euler Diagrams. Therefore, I want to again bring up the idea of merging the articles on these two topics.
Finally, I think that the diagrams used to show the union, intersection, and symmetric difference are misleading and would be better cited in connection with Euler Diagrams. A basic aspect of a Venn Diagram is that it illustrates a proposition. For example, the diagram in the article which is supposed to show the intersection, when viewed as a Venn Diagram, actually asserts, by means of shading the intersection, that the intersection is empty. Dagme (talk) 21:33, 25 February 2011 (UTC)
Powerful?
Not sure what you mean by powerful in your post above. Showing the intersection between sets can be done in other ways and Euler had it too,
Take the case as below:
we have a Set S and sets A and B and C lie wholly in set S:
1. A and B intersect. You would preferably label them as S.A, S.B and S.A.B and S.C You would never call S.A.B as S.A.B.not(C), neither S.A as S.A.not(B).not(C) and so on ... why? because the context clearly makes it obvious there is no intersection with C Hence if the diagram is not given and you are told the relative areas of S.A, S.A.B , S.B , it suffices
2. A and B and C intersect you would call them S.A.B.C and S.A.B or would you call them S.A.B.C and S.A.B.not(C), and would S.A.B imply that S.A.B.C is a subset of S.A.B? It need not be because of the inherent logic above. If i do not write another more specific item, what do you get?
That as I see is the fundamental difference between Euler and Venn and their diagrams. —Preceding unsigned comment added by 202.56.215.22 (talk) 09:53, 21 April 2009 (UTC)
I agree, without a diagram, Venn's representation has no meaning. Hark at all those teachers who think so. —Preceding unsigned comment added by 122.167.200.75 (talk) 10:16, 30 May 2009 (UTC)
The notation of A intersection B intersection Not(C) is flawed. The diagram simply helps add to the confusion. Most of the time the data is not presented as a diagram but as raw data with elements/attributes that tie it to a set. In that case there is no way one can say "this is not from that set as the set is never defined". Try a regex with A&&B, by saying A&&B!!C you are not going to get anything but A&&B!!C, which is more specific than the generic A&&B case. Note there could be a D/E/F and so on hence the methodology is flawed. -Alok 05:55, 19 April 2011 (UTC)
Venn diagrams and truth tables
My viewpoint is that Venn diagrams can be viewed more-or-less as truth tables. (Each region corresponds to one line of truth table. Perhaps this picture [1] illustrates well what I have in mind.) I think something like this could be mentioned in the article. (Although it should be sourced by literature and I did not find anything by a quick search on google books. Perhaps I did not come up with an appropriate search query.) --Kompik (talk) 12:25, 6 July 2011 (UTC)
- Ok, so after little more searching I found two references for this:
- The rows correspond to the different basic regions of the Venn diagram, eight in the case of a three-variable law like (3.5), and the corresponding input-tuples of zeroes and ones are entered consistently at the outset.
- Elements of logic via numbers and sets By D. L. Johnson, Page 62 [2]
- Using membership tables, we can establish the equality of two sets by comparing their respective columns in the table. Table 3.3 demonstrates this for the Distributive Law of union over intersection. We see here how each of the eight rows corresponds with exactly one of the eight regions in the Venn diagram of Fig. 3.8.
- Grimaldi R. Discrete and combinatorial mathematics (5ed., AW, 2004), Page 143
- --Kompik (talk) 6 July 2011
Edwards and other post-Venn diagrams
I have now seen some edits go back and forth on a link to this paper: http://mathsci.sharif.edu/mahmoodian/Papers/Generalized-Venn-Diagram1987.pdf
The paper makes it look like this group came up with Edwards' diagram by 1987. Edwards' cogwheels was published in 2004, right? Had he published the idea before these 1987 authors? Can the validity of the pdf be established?
Fanyavizuri (talk) 22:12, 10 April 2011 (UTC)
- Indeed, there is a rather critical review of Edward's book Cogwheels of Mind by Peter Hamburger in Mathematical Intelligencer [3]. I will quote just one sentence: Edwards knows that Grunbaum showed in 1975 [8] the possibility of constructing Venn diagrams with any number of convex curves, and he recognizes that this was a "remarkable advance," but he gratuitously disparages others' figures in comparison to his own, and he misrepresents the history. --Kompik (talk) 18:52, 6 July 2011 (UTC)
Stanford Article
If you read sections 2.1 and 2.2 of the Stanford article at
http://plato.stanford.edu/entries/diagrams/
you will see pretty much what this Wikipedia article should be.
Dagme (talk) 06:30, 14 July 2011 (UTC)
Non-Venn diagram with 14 versus 13 regions
I reverted the edit -- the number 13 can go back if its author is willing to add a bit of wording, to wit: To be correct and thorough we need to say the diagram has 14 regions -- 13 colored and one more non-colored region exterior to all the colored regions. This article doesn't make it clear that there are always 2^N regions for N sets; the "missing" region is the exterior (e.g. the region/minterm ~A & ~B & ~C & ~D for a 4-set diagram). Bill Wvbailey (talk) 21:56, 28 October 2010 (UTC)
- Agree: Here, and elsewhere, purported Venn diagrams for three sets frequently omit the enclosing box (or circle). Such diagrams fail to show elements (if any) that are members of none of the three sets. Thus, they cannot be considered to meet the definition of Venn diagrams. There is always a universe (a set to enclose the set of given sets), and Venn diagrams must show it explicitly. (My opinion.) David Spector (talk) 21:14, 30 January 2012 (UTC)
Recently discovered simple symmetrical 11-venn diagram "Newroz"
A recent study (July 2012) conducted by faculty of the computer science department at the University of Victoria has unearthed the very first simple symmetrical 11-venn diagram, which was named "Newroz" by its discoverers. It isn't included in the article and right now, "Newroz" redirects to an unrealted page. Its quite a discovery and I think it should be included in the article- I'm just not the mathematical sort of person to do it.
Original report: [4], more material: [5]
Musicmaster890 (talk) 02:26, 17 October 2012 (UTC)
- "Newroz" should continue to redirect to the Persian new year celebration, which is the main meaning of the word (the only meaning of the word until three months ago)... AnonMoos (talk) 05:42, 17 October 2012 (UTC)
- That's certainly reasonable. I won't pretend to understand any of the nuances of the Persian culture of language, but the article title for the new year celebration is spelled differently ("Nowruz"), so perhaps there should be a "'Newroz' redirects here" link its header. Alternatively, there is a disambiguation related to the page. Musicmaster890 (talk) 12:06, 17 October 2012 (UTC)
Diagram Venn_diagram_showing_Greek,_Latin_and_Cyrillic_letters.svg
The diagram shown is a little misleading since K and Y occur in Greek, Latin and Russian. The Russian letters depicted seem to have slightly different typography but they are the same character/symbol in each case and are written by hand identically. 84.154.138.142 (talk) 21:36, 19 September 2013 (UTC)
New Section: Popular Misconceptions
I was watching Seth Meyers debut on the Late Show and was stunned by his sketch "Venn Diagrams". In the sketch, he showed two circles with titles then the circles merged toward each other until they overlapped and intersected and the intersection area was labeled with a new title. It was intended to be funny, and a few of the items were. Some critics claimed the sketch went on too long and wasn't funny.
The real problem was the sketch's blatant mis-portrayal of Venn Diagrams. Instead of showing the intersection, most of the humor was derived from finding a common category that both titled circles fit into. In one example, the two circles were labeled “Russia” and the “The NBA”. The animation moved them to overlap and the intersection area was revealed to be “Places that are more gay friendly than Arizona”, clearly showing a category to which both Russia and the NBA could belong. The segment included nearly a dozen examples, most of which continued the error, showing a category to which the items had common membership, instead of the intersection. One notable correct example was "Men that wear fedoras" and "Men that are cool" intersecting to reveal "Indiana Jones".
When I scanned the internet to find others like me that we stunned by the error, I found nothing. I thought Venn Diagrams were something very clearly understood even by people with only limited interest or ability in mathematics, but apparently I was wrong. After reading the Talk: Venn Diagram section, I think there's a case for a section on the Wikipedia page for Popular Misconceptions. The often ignored requirement for a Universe box could be mentioned etc.
What do you think? — Preceding unsigned comment added by Dankdyer (talk • contribs) 08:00, 27 February 2014 (UTC)
pseudo-Venn diagrams
Aside from Wikipedia, the top Google text & image hits for "Venn diagram" are predominantly incorrect (e.g. [6] [7] [8] [9] [10] [11]. There seems to be a proliferation of k-12 teaching aids that create interlocking circles to compare/contrast concepts, and call this a Venn diagram. I'm pretty strongly opposed to hijacking a well defined term & publishing incorrect examples with such high profile. Is anyone familiar with the term for the concept that is represented? Ripe (talk) 01:07, 18 February 2009 (UTC)
- I looked at whales and fish and I have to second the motion. However, we aren't doing that. Perhaps you could keep a vigilant eye out.Dave (talk) 02:37, 26 December 2009 (UTC)
- as far as I can tell, (a) Venn, in Symbolic Logic, did not seem to intend the diagrams to be restricted to one particular kind, (b) although there are a lot of assertions as to what Venn Diagrams represent I also find plenty of evidence that what kinds of things they can represent is not even necessarily a part of what defines a Venn Diagram, which is instead a form with many possible interpretations (supported by his presentation of them), except that (c) a Venn Diagram does, in some sense, always represent a notion of a set, simply by the form it takes (unless it was completely malformed and without sense) and, therefore, whatever names one might apply to the entities, they would meet this, tautological, idea of Venn diagrams representing sets and set membership.
- I took at look at the first of the links mentioned (www.learnnc.org/lp/pages/2646) and after going through it, I think it's actually a very well done page. (the author is giving teachers ways of exploring similarities and differences between entities, and actually is using the initial "Comparison" diagrams to lead up to reasons to use "Classification" Venn diagrams instead, walking the reader through adding entities and the increased complexity, including the difficulties of dealing with more than 3 entities with circles, and then demonstrates how the 4-or-more-entity case is handled much better by the "Classification"-style diagrams, and the article does more-or-less seem to be in congruence with OP Ripe's view that these aren't truly Venn diagrams, stating: "The truth is, this is not a Venn diagram. Mathematically speaking, a Venn diagram represents sets and elements."
- I haven't finished reading Venn's Symbolic Logic yet (which I found in archive.org's repo) but Venn's purpose in introducing the diagrams was to help clarify logical problems... he seems to have been a pragmatic sort that was looking for alternative and easier ways to understand syllogistic and other logical issues, and he introduced his diagrams (contrary to some other assertions elsewhere on the Talk page) in response to some deficiencies in Euler diagrams, and within the first few pages of introducing the diagrams, he showed (or at least attempted to show) a full equivalence between (properly understood) syllogistic logic, predicate logic, and set memberships. Additionally, although I haven't done an exhaustive search, it seems the form of the Venn Diagram is, in at least some cases, considered to be what defines it, e.g. see the first paragraph of "Exact and Approximate Area-proportional Circular Venn and Euler Diagrams", with a more flexible notion of the interpretation than most of the lay resources, and many of the mathematical and logical resources, assert. (e.g. Venn Diagrams representing, and only representing, sets and set membership and operations.) So, even if we accept that the 'Comparison' form of the diagram isn't about set membership, I don't think that would necessarily be a strong objection to calling something else with the form and idea of inclusion/exclusion etc. of a Venn Diagram a Venn Diagram.
- And further, I don't see any problem with (just as in the 'Classification' form of the Diagram in the learnnc.org reference uses, say, "Has Fins", and "Lives in Water", as shorthand for "The Set of Animals that Have Fins" and "The Set of Animals that Live in Water") simply re-framing, say, "Whale" and "Fish" as "The Set of Predicates that obtain for Whales" and "The Set of Predicates that obtain for Fish". In other words, just define a Venn 'Comparison' Diagram as one that solely uses sets with a name of 'X' to mean 'The Set of Predicates that obtain for X' and define a Venn 'Classification' Diagram as one that solely uses sets with a name of 'X' to mean 'The Set of Entities of type X' or something similar.
- So, as far as I can see: (a) it's at least possible, if not likely, that there is nothing that says the entities represented by the shapes (generally, but not required to be circles) in a Venn Diagram must be sets, and (b) it's a misunderstanding to think that there's a particular type of set that must be represented; the first cases Venn dealt with in the version of the book I am looking through were based upon clarifying syllogisms, and he used circles of A and B to represent subject and predicate. And, in fact, upon a quick reading of those first few examples, it seemed to me that he was showing that you could represent, say, "some types of fabric are soft" with two circles, overlapping, with one representing "types of fabric" and one representing "soft things". Actually it's a bit more complex than this; he does explicitly say that the 'some' used in his diagrams is "some, but not all" as opposed to the usual syllogistic meaning, and he also covers that without knowing also that there are some soft things that are not fabric you would have to show your ignorance by giving a choice of either the two overlapping circles, or the "soft things" circle completely within the "types of fabric" circle; so, for instance, the syllogism might be better stated as "some (but not all) types of fabric are soft (and some soft things are not fabric)". Regardless; here we have one circle representing a type of object, then one circle that represents a set of things that have a certain property; the first corresponding to the "Whale" and "Fish" sets of a Venn 'Comparison' Diagram, and the second corresponding to the "Has Fins" and "Swims" in a Venn 'Classification' Diagram.
- In other words: from the get-go, it looks quite arguable that Venn intended the diagrams to be able to handle *at least* those cases (and didn't even restrict them to containing solely one of them or solely the other); therefore, I see little support for the claim that one or the other type of entity is the 'proper' one for a Venn Diagram, and, I would expect that we could come up with even more types in addition to the examples we have, thus far, of Venn 'Comparison' Diagrams, Venn 'Classification' Diagrams, and, say, Venn 'Syllogism' Diagrams. And really, I think that this is part of the power of the Venn Diagram: you can re-frame the problem in manners better suited for whatever logical structure you are trying to capture: if comparing, say, sea mammals and fish, and twenty attributes of animals, the 'Comparison' chart would be quite simple, and the 'Classification' a dreadful mess. And, conversely, if you're classifying animals solely based upon whether they are 'carnivore', 'omnivore', or 'vegetarian', and you have twenty different animals, the 'Comparison' form would be a dreadful mess. And if you were trying to capture a syllogism, or, say, a simple first-order predicate logic argument, you would be hard pressed to make much sense out of it if you were restricted to either of those two.
- Shelleybutterfly (talk) 18:16, 25 March 2014 (UTC)
- as far as I can tell, (a) Venn, in Symbolic Logic, did not seem to intend the diagrams to be restricted to one particular kind, (b) although there are a lot of assertions as to what Venn Diagrams represent I also find plenty of evidence that what kinds of things they can represent is not even necessarily a part of what defines a Venn Diagram, which is instead a form with many possible interpretations (supported by his presentation of them), except that (c) a Venn Diagram does, in some sense, always represent a notion of a set, simply by the form it takes (unless it was completely malformed and without sense) and, therefore, whatever names one might apply to the entities, they would meet this, tautological, idea of Venn diagrams representing sets and set membership.
recently added animation
The animation looks a big off topic to me as it essentially has nothing to with venn diagrams as such but is rather an alternative illustration of sets and set operation. Note that this is an article about a specific illustration tool called venn diagram and not an article about sets and set operations where different illustration may improve the understanding of the reader.--Kmhkmh (talk) 23:34, 8 April 2016 (UTC)
- I agree, it seems off topic. I'm debating reverting it. DavidHobby (talk) 02:05, 9 April 2016 (UTC)
- Let me argue, why I do not find my illustrations off topic: Venn diagrams make visible logical relations by specific patterns. You can "see" the logical relation by looking at a Venn diagram. This is what my illustrations foster, too. Furthermore, my illustrations explain how Venn diagrams work and why they look like they look: because logical operations are applied pixel-wise.
- They're nice animations, but I think the bottom line is that "if it doesn't have circles, it's not a Venn diagram". (Which isn't quite right, the insides of curves other than circles are fine.) I looked around a bit, and couldn't find a really good place to put the animations. "Bitwise operation" seems best, but the page is already organized around bitwise operations in the sense of assembly language. There's also "raster graphics". Got me. Just because you've got the animation, that doesn't necessarily mean there's a home for it on Wikipedia?DavidHobby (talk) 23:10, 10 April 2016 (UTC)
- The animations do not show sets as sets of points inside a curve. Therefore they are not Venn diagrams, and do not belong on this page. O.K.?DavidHobby (talk) 11:53, 11 April 2016 (UTC)
- Not really. There are other examples in the article that do not qualify according to your definition (which seems too strict to me). The very first example consists of three curves with objects (glyphs) surrounded by them. Isn't it distracting that we have two kinds of objects here: the points of the curves (continuous) and the glyphs (discrete)? The next two sets in the article are represented by two coloured circles: colouring seems to make things clearer. Could you please explain what makes my illustrations worse than these examples?
- No, I just went and checked. All the pictures show sets as the interiors of curves, except for the "Extensions to higher numbers of sets" section. In the example you mention, the glyphs are the elements, and the circles are the sets of letters used in various languages. There are two kinds of things, sets and their elements, so of course they are symbolized in different ways. Sorry, I can't make it clearer: The animation is NOT a Venn diagram, because it does not represent sets as regions inside curves. There are no closed curves in the animations?! DavidHobby (talk) 02:18, 12 April 2016 (UTC)
- I will add curves and hope the illustrations will qualify then. The illustration for the intersection will look like this. If the reader wants to he can watch the animated version which makes clear that intersection corresponds to pixel-wise logical conjunction (AND).
- I will add curves and hope the illustrations will qualify then. The illustration for the intersection will look like this. If the reader wants to he can watch the animated version which makes clear that intersection corresponds to pixel-wise logical conjunction (AND).
- No, I just went and checked. All the pictures show sets as the interiors of curves, except for the "Extensions to higher numbers of sets" section. In the example you mention, the glyphs are the elements, and the circles are the sets of letters used in various languages. There are two kinds of things, sets and their elements, so of course they are symbolized in different ways. Sorry, I can't make it clearer: The animation is NOT a Venn diagram, because it does not represent sets as regions inside curves. There are no closed curves in the animations?! DavidHobby (talk) 02:18, 12 April 2016 (UTC)
- Not really. There are other examples in the article that do not qualify according to your definition (which seems too strict to me). The very first example consists of three curves with objects (glyphs) surrounded by them. Isn't it distracting that we have two kinds of objects here: the points of the curves (continuous) and the glyphs (discrete)? The next two sets in the article are represented by two coloured circles: colouring seems to make things clearer. Could you please explain what makes my illustrations worse than these examples?
- The animations do not show sets as sets of points inside a curve. Therefore they are not Venn diagrams, and do not belong on this page. O.K.?DavidHobby (talk) 11:53, 11 April 2016 (UTC)
- They're nice animations, but I think the bottom line is that "if it doesn't have circles, it's not a Venn diagram". (Which isn't quite right, the insides of curves other than circles are fine.) I looked around a bit, and couldn't find a really good place to put the animations. "Bitwise operation" seems best, but the page is already organized around bitwise operations in the sense of assembly language. There's also "raster graphics". Got me. Just because you've got the animation, that doesn't necessarily mean there's a home for it on Wikipedia?DavidHobby (talk) 23:10, 10 April 2016 (UTC)
 — Preceding unsigned comment added by Marble machine (talk • contribs) 10:54, 12 April 2016 (UTC)
— Preceding unsigned comment added by Marble machine (talk • contribs) 10:54, 12 April 2016 (UTC)
- Sorry, that doesn't work. A Venn diagram consists of different regions that partially intersect. Of the three pictures, only the middle one fits. The other two only have single regions, and so can only show two sets, which would be A and A^c in the one on the left. Also for a Venn diagram to be readable, it should be easy to follow by eye the borders of the regions. That's why circles are used, instead of your bar and cross. DavidHobby (talk) 04:22, 13 April 2016 (UTC)
- I agree with Kmhkmh and DavidHobby, the content of the illustrations is off-topic. And the animations are distracting, the concepts could be achieved with still diagrams (perhaps with the same graphical conceit -- the beads are fine; just don't make them move, they move too fast, you can't figure out what they're doing). Perhaps they belong in a 2-valued (e.g. Boolean) logic article, but you may get some pushback because of the animation. BillWvbailey (talk) 16:05, 11 April 2016 (UTC)
- I agree: maybe the beads move too fast. But only by their movement the fact can be made visible that the resulting image is generated by pixel-wise logical operations
Cyrllic
The letters being displayec are the variants specific to the modern Russian language - not, for example those used in for Ukrainian, Bulgurian or Old Church Slovanic. TomS TDotO (talk) 05:01, 7 May 2016 (UTC)
New picture proposal
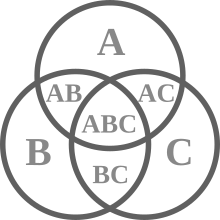
I created the image ABC Venn Diagram.svg, which you can see on the right, and I feel that it better illustrates the article than the picture currently there. First of all, it's colorless, so there are no worries about confusion about what a Venn diagram is, something that other people on this talk page were worried about.
What are your opinions? Do you think my image would be more appropriate? Is it too simple?
If it's not too simple, and we are going to implement it, then how would we do so? I think we should replace the image at the top of the article with it, and give it a caption along the lines of that which accompanies the image on the right. What do you think? - − Elecbullet (talk) 03:00, 28 September 2009 (UTC)
- In Venn diagrams the circle A is on the left, and the circle B is on the right side. Everything else would be confusing. When a third circle C is added - usually below them - that shouldn't change the position of the two circles already used. Lipedia (talk) 02:16, 20 December 2009 (UTC)
- Actually the drawing is not technically correct. For example, the left-intersecting AB should be AB~C (A & B & ~C) where ~C signifies "NOT C". And the diagram needs ~A~B~C on the outside/exterior region. (From a graphics-art standpoint I would prefer that you tone down the thickness of the circles). See the drawings, both historical and modern, at Euler diagram. Bill Wvbailey (talk) 14:45, 20 December 2009 (UTC)
- I think the drawing is technically correct. You are normally given data without a diagram and one would interpret data or assign data to a set based on given data in a format similar to the above diagram. The "nots" are too many to have given data. -Alok 05:56, 19 April 2011 (UTC)
- I don't fully agree to that. It's obvious, that diagrams like File:Intersectionsets.png are wrong, because they simply call an area which is in fact . But when the letters are used without the signs, I think its nothing wrong about this way. I've also done this way in File:Syllogism-Set-Diagrams.jpg. Lipedia (talk) 15:39, 20 December 2009 (UTC)
- p.s.: How would the last sentence read in good grammar? Lipedia (talk) 15:43, 20 December 2009 (UTC)
- Historically there have been serious issues with "syllogisms" and the misuse and abuse of Euler diagrams, as spelled out in Euler diagram; for this reason they were abandoned by serious logicians after Venn. For example the concatenation of two symbols A and B i.e. " AB " has no meaning with respect to either set theory or logic unless you define what the concatenation means operationally, and it is easily confused with a tacit conjunction or logical AND; in particular " AB " in Boolean algebra means "A*B", where * means "arithemtic multiply", or it can mean "A AND B" in both math and engineering usage, where AND is the logical AND, etc, etc.
- Agree to the above, and it is logical to assume there is no "not" because the case is more specific. 192.18.192.21 (talk) 05:54, 19 April 2011 (UTC)
- In a deeper sense, the problem has to do with specifying a domain of discourse, i.e. the "universe" or "box" that explictly or implictly surrounds/contains the three circles. Your domain/universe of discourse is three "sets" A, B, and C, not just two (i.e. A and B). So when confronted with a region labelled " AB " we have to ask ourselves -- what has happened to set C? In the three-set domain of discourse, region A ∩ B implies the union of two regions (A ∩ B ∩ ~C) U (A ∩ B ∩ C) = A ∩ B ∩ (~C U C) = A ∩ B. In other words, A ∩ B actually comprises two regions, not one. This is exactly what happens when we are considering Boolean-like variables, i.e. (A & B) = ((A & B) & (~C V C)) = ((A & B & ~C) V (A & B & C)).
- To conclude, the drawing as it stands is misleading. We want our exposition to be as precise and accurate as it can possibly be, even at the expense of a "simplicity" that causes confusion or flatout misunderstanding.
- I think this drawing is more accurate because of the reasons mentioned above. It clearly demarcates what belongs to what set.-Alok 05:58, 19 April 2011 (UTC)
- p.s.: "But when the letters are used without the signs, I think there is nothing wrong with this method of labelling."
- Bill Wvbailey (talk) 23:07, 20 December 2009 (UTC)
- Hello there. I appreciate the nice diagram in this section. And, I appreciate all the statements of what area is what in the notation of symbolic logic. May I also assert, speaking as a technical writer, if you put this diagram or that notation in, the average reader will have no idea under the sun of what we are talking about, and most of the college graduates in any other discipline but logic will not either. So, no one will bother with it, and it will be of use to no one, as the few who would understand it would not need it. The color diagram is nice. It should stay. It is not suitable for color blind persons. Here is what I recommend. Redo the diagram in this section so that the circles match the ones in the color diagram. Then present this one as an explanation of the color one just below it. This is for the diagram. I do not yet have any ideas on the notational descriptions.Dave (talk) 01:52, 26 December 2009 (UTC)
- Bill Wvbailey (talk) 23:07, 20 December 2009 (UTC)
- Dave, here is how the drawing's regions should be labelled to be technically correct. This is cc'd from Euler diagram (for more, see that article):

- I had an idea. Maybe if we used a Venn diagram with TWO parts instead of three it would be simpler to understand. How's that sound? I could quickly turn my three-part Venn Diagram into a two-part one, then upload it separately. Later though. I have to write a thank-you note for a UConn sweatshirt. − Elecbullet (talk) 04:06, 6 January 2010 (UTC)
- ...And if I'm going to do that, what changes should I make? − Elecbullet (talk) 04:08, 6 January 2010 (UTC)
- For a two-variable drawing the center region would be AB, the left would be AB' and the right would be A'B and the outer region would be A'B' (the symbols having the same meanings as above). Actually, a progressive display of drawings would be useful: a single circle A with background (universe of discourse) A', single circle B with background (universe of discourse) B', the A,B pair of circles drawn overlapping in the conventional manner. Then shade the regions to indicate an included region (some folks shade to include, some folks shade to exclude). For N topics of discourse i.e. N = 2 for { A, B } there are 2^(2^N) possible shading patterns, so even for the simplest case we have 4 drawings { null, A, A', A+A'= U }, and for { A, B } we have 16 possible drawings ( null, AB, A'B, AB', A'B', AB+A'B, AB+AB', AB+A'B', A'B+AB', A'B+A'B', AB'+A'B', AB+A'B+AB', AB+A'B+A'B', AB+AB'+A'B', A'B+AB'+A'B', AB+A'B+AB'+A'B' = U } i.e. { 1 null, the 4 minterms, 6 pairs of minterms, 4 triples of minterms, 1 universe }, (note this number pattern 1, 4, 6, 4, 1 derives from Pascal's triangle). Clearly the number explodes after N=2 (N=3 yields 256 possible patterns, N=4 yields 65,536 possible patterns).
- After I wrote the above paragraph I looked at Karnaugh map and observed that the writers do exactly what I described above -- they display all 16 maps for 2 variables, and observe that they actually invoke a Venn diagram and label the regions. As the Euler diagram article suggests, really a Karnaugh map is just a redrawing of a Venn diagram, i.e. they are for all practical purposes identical. So the Venn drawings would be repetitive . . . one of the problems of Wikipedia is exactly this, that the articles don't tie together in a coherent manner i.e. in historical order: Syllogism, Euler diagram, Venn diagram, Truth table, Veitch diagram, Karnaugh map, Quine-McCluskey algorithm, etc. I suppose repetition is okay. (Download Venn 1881 from google books, if you can't find it I'll get the link for you; it may be of some use here). Bill Wvbailey (talk) 16:15, 6 January 2010 (UTC)
You are wrong in mixing up a Karnaugh map with a Venn Diagram. The Karnuagh map makes certain assumptions:
1. A has 2 states 0 and 1
2. it tries to imply 0 is A'
When one makes K maps, we tend to write 0 and 1 and not A and A', if it was tri-state you would tend to write 0 , 1, and 2 perhaps and group accordingly. The notion of A'.B simply means A is 0 and B is 1. It does not in any way apply any intersection, union and so on. Do not try and confuse A'B as an intersection of not A and B. Treat it as high and low levels etc. Formal grouping was not the agenda of Venn Diagrams. 122.178.238.114 (talk) 05:20, 16 February 2014 (UTC)
So if we have a LED that goes on when A is on, we do not need to wire it to the not B and not C cases. we simply wire it to A. We have to explicitly do the B and C case when the "state" is A.B'.C'
The diagram is a contradiction to the wiki's own statement:
The intersection of A and B is written "A ∩ B". Formally:
x ∈ A ∩ B if and only if
x ∈ A and
x ∈ B.
- ...Here I was thinking Venn diagrams were simple. Uhm. Sorry, I don't understand exactly what you want, I'm just a 14-year-old-kid with no college degrees or anything. What do you mean "an included region"? − Elecbullet (talk) 00:35, 9 January 2010 (UTC)
I agree with this representation, given a diagram it is right
The word intersection also can have a meaning only when there is a diagram.
For example, let me spell the question
A intersection B intersection C = 4
Now, this does not tell me if there is a D,E,F etc that exists in the diagram? correct?
So without a diagram is it not valid to assume that A intersection B intersection C is the same as A intersection B intersection C not (everything else??)
In other words, the above description is valid if only a diagram is given.
If there is any exam paper which asks one to make a judgement based on only the given data without a diagram, it is valid to assume that there are 3 regions A,B,C and we are referring to the intersection of all 3 regions.
likewise A intersection B is only the region common to A and B given we are giving A intersection B intersection C a different tag, (else you could question the validity of what is "A" in the 1st place.
The diagram is perfectly right in that sense.
It is just like saying
"i do not know if A intersection B not C implies D , E, F does not exist without a diagram".
I mean if the logic works this way, it works that way too (the not case too)
Either ways without a diagram the question is flawed.-Alok 05:56, 19 April 2011 (UTC)
Also note that the wiki and othet literature define intersection as follows:
The intersection of A and B is written "A ∩ B". Formally:
x ∈ A ∩ B if and only if
x ∈ A and
x ∈ B.
so if 1 says x ∈ A ∩ B includes (superset of) x ∈ A ∩ B ∩ C; it means there is an x ∈ A and x ∈ B and x ∈ C then the "only if" is not satisfied in the way intersection is defined.
So if one says x ∈ A ∩ B , the not C,D,E,F is already implied, so to denote x ∈ A ∩ B ∩ ~C and x ∈ A ∩ B ∩ C in a separate manner would be futile,infact making it unclear.
One would simply call the 1st case x ∈ A ∩ B and the second as x ∈ A ∩ B ∩ C -Alok 05:56, 19 April 2011 (UTC)
Any DBA using the intersect operator will understand this well.MySQL would call it inner join and not intersection. The formal definition of intersection in a domain would imply only those sets exist. So A intersection B would not include elements in C because of the if and only if clause. Some databases call the operator inner join and drop the keyword 'intersection'. — Preceding unsigned comment added by 122.166.89.154 (talk) 17:09, 28 September 2016 (UTC)
http://www.cut-the-knot.org/do_you_know/add_set.shtml#intersect — Preceding unsigned comment added by 122.166.89.154 (talk) 17:20, 28 September 2016 (UTC)
Definition of U?
A Venn diagram must always have a rectangle around it indicating the underlying so-called universal set U. Further, the letter U is used in the fourth image to "explain" the complement without it being defined. (It is as if we are writing "We have the function f(x)=x." without defining the domain.) In every Venn diagram, it is important to always have the rectangle and a U since this (implicitly) explains that sets and their elements "live" in some space. Venn diagrams are introduced at age 5 and having a rectangle, not having a rectangle confuses our children from the start. I think this is easy to fix. My suggestion would be to define the universal set, say that it is usually denoted by the letter U and then add as first image a rectangle labeled U and a oval for a set A with points in it and outside of it. (I will try to create an image and post it here within a week.) (I am surprised that the Wikipedia higher math police patrol has not complained :). I know they don't care about children, but they are always so nitpicking about articles being absolutely mathematically correct.) Lfahlberg (talk) 07:03, 19 March 2014 (UTC)
- You are correct. To be sure it's not in the article now I loaded the text of the article into a Word document and searched for "universe", "domain", and "discourse" and turned up "no matches". Another Wikpedia article comes up short.
- The notion isn't new-fangled. As I recall that it goes back at least to Boole 1848; indeed it does (probably back further):
- "Now whatever is that range of things to which our discourse is confined, and from which all the things that we discourse of are taken -- that range of things we shall define as the Universe of Discourse" (Grattan-Guinness and Bornet 1997:4ff. Quote taken from Boole's The Nature of Logic (1848), section "Of the limitations of the subject of discourse". Editors Ivor Grattan-Guinness and Gerard Bornet, 1997, George Boole: Selected manuscripts on Logic and its Philosophy, Birkauser Verlag, Basel, Switzerland).
- Also see the illustration (photograph) of the page from Couturat 1914 appearing at Euler diagram.
- Here are two more-modern definitions, the first with regards to the propositional calculus, the second with regards to predicate calculus:
- "We shut off debate about these issues [e.g. "x loves y" when x = carrots and y = beans] . . . by assuming that there is a particular nonempty set or collection of objects, called the domain D, over which each of the independent variables of our propositional functions ranges; i.e. the members are the objects to be allowed as values of the variables.
- "This is not at all a trivial assumption, since it is not always clearly satisfied in ordinary discourse. In mathematics likewise, logic can become pretty slippery when no D has been specified explicitly or implicitly, or the specification of a D is too vague."(italics in original: Kleene 1967:84. Stephen Cole Kleene, 1967, Mathematical Logic, Dover Publications, Inc. Mineola, New York.)
Kleene extends this to the predicate calculus [where two variables appear in a simple sentence e.g. "x loves y" rather than "x loves Mary", and the notions "for all" and "there exists" are added to the treatment]:
- "The domain D for an application of the predicate calculus may also be called the universal set or the universe or universe of discourse. It is to be simply a set, fixed for the given application, which contains as members all the objects which we are considering in that application.(Kleene 1967:135ff)
- In this Venn-diagram article the lead illustration is therefore wrong. But the illustration "Venn diagram as a truth table" is correct; it shows 000 as the element outside the intersecting rings; the universe of discourse (domain of discourse, domain) U then contains all 8 possible elements {000, 001, . . . 111}. And the notion is alluded to (obscurely, without definition of "U") in the far-right illustration in the series of red-white illustrations; this red-colored U outside the circles shows why this region is important -- it allows the logical NOT): "All things (winged creatures?) not an A (mammal) or a B (a bird)", for example would -- if we're discussing all living things -- include ~A & ~B "flying insects"; but if our universe of discourse (function-domain) is "all winged things" it would have to also include e.g. "winged statues" (e.g. "Pegasus") and "airplanes" and imaginary things ("flying pigs") so forth [Boole mentions this idea too: "Sometimes we speak of things which do not exist, but are the mere products of the imagination as when we say The centaur is a fabulous being" (ibid)]. So the reason U is so important is that it pins us down as to what we're really discussing, not what we think we're discussing (e.g. the "slippery-slope" quotation from Kleene).
- As to how to fix the article . . . this would require a search into Venn's writing. Probably a whole new section discussing the notion, with some history. And a new illustration of a single circle inside a rectangle, the circle labelled "A" for example and the universe labelled "NOT-A". Anyway, that's my thinking. BillWvbailey (talk) 15:53, 11 April 2016 (UTC)

- Here's a candidate drawing of a universe (domain) of discourse showing the two basic regions of discourse relative to an assertion, "x has wings", "It's not the case that 'x has wings'". Is this how we want to illustrate "the domain of discourse" for this article? Have I got this right? comments? BillWvbailey (talk) 18:39, 11 April 2016 (UTC)
- Yes, it looks good. As an aside, the "Higher math police" have probably been neglecting this page because they all know what a Venn diagram is, and don't need to look here? Until earlier today, the article didn't even define what a Venn diagram was in the first paragraph, it just gave a bunch of examples. So I don't care about the universe of discourse issue. Yes, that's the point of the rectangle, its interior represents the universal set. The candidate drawing looks fine to me, and I don't see a problem with it not matching the other pictures graphically. They're all quite different anyway. — Preceding unsigned comment added by DavidHobby (talk • contribs) 02:08, 12 April 2016 (UTC)
If you google "Venn diagram" you see, first, a google-definition (see in sub-section, below) and second, this Wikipedia article comes up first in the search (surprise, surprise). So everyone (e.g. school-kids) who are puzzled about Venn diagrams will end up at this article. Two serious omissions are these, the second in my mind being really important; it appears only in the quote from Cantor at Set (mathematics):
- A Venn diagram is different from an Euler diagram in part because of the requirement for a specified domain of discourse U.
- The "elements" that we include in the domain of discourse U are not real objects, but rather concepts or generalizations of real objects. So we don't sneak into the zoo to nab three zebras and two parrots and a flamingo and four snakes, put them in a common pen, and call this a mathematical set of zoo animals, but rather we collect their thought-objects { zebra, parrot, flamingo, snake } and put them in a thought-pen that we think of as "zoo animals". Only if the zebras are thought of as distinguishable could their concepts { fat zebra, skinny zebra, scared zebra } be considered elements of the set of thought-things (concepts) to which we apply the label "zebras_stolen_from_the_zoo". Dedekind makes this quite clear, the keyword here being "thought":
- "In what follows I understand by thing every object of our thought. ... A thing is completely determined by all that can be affirmed or thought concerning it. A thing a is the same as b (identical with b), and b the same as a, when all that can be thought concerning a can also be thought concerning b, [and vice versa].
- Given these thought objects, Dedekind forms the notion of a "system S" (modern set), itself a thought-object:
- ". . . different things a, b, c . . . can be associated in the mind and we say that they form a system S; we call the things a, b, c, . . . elements of the system S, they are contained in S; conversely, S consists of these elements. Such a system S (an aggregate, a manifold, a totality) as an object of our though is likewise a thing (1) [sic]; it is completely determined when with respect to every thing it is determined whether it is an element of S or not.*" (Dedekind 1893:45. The * references a bone of contention with Kronecker that Kronecker failed to answer; the meaning of (1) is unclear. from "The Nature and Meaning of Numbers", a reprint of the second edition 1893 appearing in Essays on the Theory of Numbers, 1963, Dover, Mineola NY, ISBN 0-486-21010-3)
As I write this I am becoming confused myself: the relationship between the notions of set union ∪ and set intersection ∩ versus logical OR and logical AND yielding truth-values of statements about the "thought objects" that form the universe of discourse.
I haven't decided how, and even if, to proceed. One place to start is to fix the lead sentence:
Lead paragraph wording: universal set as critical part of the definition
I googled "Venn diagram" and got this as the definition -- front and center:
- "a diagram representing mathematical or logical sets pictorially as circles or closed curves within an enclosing rectangle (the universal set), common elements of the sets being represented by the areas of overlap among the circles."
This seems to me a very nice definition. BillWvbailey (talk) 15:40, 14 April 2016 (UTC)
- It's not a bad definition. On the other hand, having multiple correct definitions on the internet might be a good thing? The current one isn't bad either, except that "logical relations" is vague. To me, Venn diagrams "show all of the possible combinations of membership/non-membership in the diagrammed sets". Except that's too clunky to lead an article with.
I agree in general that the role of the universal set should be made clearer. DavidHobby (talk) 00:51, 15 April 2016 (UTC)
---
- Aren't the 2^N regions showing all the minterms of the N "literals" ("literal symbols": Venn actually uses these words!)? The reason I write that is because (i) aren't there are 2^(2^N) (combinations?) relations among the variables in disjunctive normal form, e.g. a*b V ~c is a relation between the 3 variables, and (ii) yesterday I was skim-reading Venn's 1881 and observed that he used darkened regions to remove regions from consideration.
- I guess, the term "combinations" is vague. It's hard to have a perfect one-sentence definition.
- Shading regions to exclude them: I haven't studied this enough to know exactly what he's up to; it seems like disjunctive normal form. For example: Venn shows a diagram of three intersecting rings (p. 105) and then he writes:
- “What we do then, is to ascertain what classes are negatived [sic] by any given proposition, and proceed to put some kind of mark against them in the diagram. For this purpose the most effective means is just to shade them out. For instance, the proposition 'all x is y' is interpreted to mean that there is no such class of things in existence as ‘x that is not-y', or xy’. All that we have to do is to scratch out that subdivision in the two-circle figure.” (p. 112 in John Venn, 1881, Symbolic Logic, MacMillan and Co., Cambridge University Press)
- He's shading things to exclude them, so the unshaded regions correspond to the desired set. That's a typical way to use a Venn diagram, although a lot of people have the shaded regions correspond to the desired set. Either works. Anyway, this would go in the History section, if anywhere?
- To the first point about minterms, Venn writes about his diagram with 3 circles (without the enclosing box; see the RE below):
- "These of course correspond precisely to the eight combinations given by the three literal symbols xyz, syz’, xy’z, xy’z’, x’yz, x’yz’, x’y’z’ [Venn uses a bar over the literal symbol to indicate NOT]. Put a finger upon any compartment, and we have a symbol name ready provided for it; mention the name, and there can be no doubt as to the compartment thereby referred to.
- You seem to have typos in the above? I'd say it would be " xyz, xyz’, xy’z, xy’z’, x’yz, x’yz’, x'y'z, x’y’z’ ". Note that he is explicitly mentioning x'y'z', which is the region outside all the circles. Using a rectangle around the whole mess of circles may be a modern innovation, but it does give one a clear place to write x'y'z'.
- "Both schemes, that of letters and that of spaces, agree in their elements being mutually exclusive and collectively exhaustive . . .".(p. 105)
- I like this point about "mutually exclusive and exhaustive"; it should be put into the article -- that all the "dots" in the domain have to go somewhere, and they cannot be duplicated, i.e. appear in more than one region.
- RE Universe of discourse: If I'm reading him correctly, Venn does not endorse the notion! In fact his drawings of 3 intersecting circles, and 4 and 5 interesting ovals, do not have a "box" around them. He points the finger toward De Morgan:
- The use of this word universe was first made familiar by De Morgan [1], but the conception itself is one that is suggested at more than one point in the traditional treatment. For instance the doctrine of a summum genus is connected with the present enquiry . . .." (p. 182, footnote [1] refers to Camb. Phil. Tr. VIII. 880.)
- And then he writes on p. 188 what sounds to me like a disavowal of the notion:
- "I cannot therefore agree with Mr Macfarlane (Algebra of Logic, p. 29) that "Every general proposition refers to a definite universe, which is the subject of the judgment... For example, 'All men are mortal' refers to the universe 'men'. 'No men are perfect', refers to the same universe". I prefer to say that there is no indication here of what the universe may be . . .."
- Yes, but that doesn't mean that he doesn't believe there's a universe. He's saying it's hazy what exactly it is. Which seems a perfectly fair position to take. In a practical situation, people would have to explicitly agree on what the universe was when that came up. But in an abstract situation, leaving it undecided saves work. DavidHobby (talk) 14:37, 15 April 2016 (UTC)
- Anyway I am even more confused than before. I haven't looked at the work of De Morgan. But I have looked at Boole. And Jevons. And by Couturat 1914 it appears the notion of "universal set" is well-established, and the Venn diagram as well (but the shading??). And to think that I thought I knew what a Venn diagram was . . .. BillWvbailey (talk) 13:34, 15 April 2016 (UTC)
- Wow, didn't realize the amount of discourse around this. I would posit that at least in wikipedia terms, we should illustrate the concept more. Most people today when dealing with set theory recognize a box around a couple circles to be just as valid a venn diagram with no box representing the Universal set. Regardless I smell better fodder for an academic paper here...128.138.65.226 (talk) 02:23, 7 June 2018 (UTC)
Example for the Venn's construction for six sets
Could someone please add an example for the Venn's construction for six sets? Thanks --Backinstadiums (talk) 13:54, 11 July 2019 (UTC)
Introduction too technical
I added a "too technical" tag referring to the article's lede (lead paragraph; introduction). The introduction can probably be modified without to much trouble so that the average reader can understand it. I'm not well-versed in this area so I defer to those of you who are to make the changes. Thanks! - Mark D Worthen PsyD (talk) (I am a man. The traditional male pronouns are fine.) 13:43, 27 September 2019 (UTC)
Evolution
Variance Kettyandsegev (talk) 06:54, 11 June 2020 (UTC)
A Commons file used on this page or its Wikidata item has been nominated for deletion
The following Wikimedia Commons file used on this page or its Wikidata item has been nominated for deletion:
Participate in the deletion discussion at the nomination page. —Community Tech bot (talk) 13:23, 11 June 2020 (UTC)
Suggestions for improvement from User talk:Dagme
(Transferred by RupertMillard from main article namespace:)
My previous editing was almost immediately undone. I will not submit another editorial effort.
I suggest instead that this article be locked and that an expert be solicited to contribute a completely new and correct article. I recommend Frank Ruskey for this. He already has published an extensive survey of Venn Diagrams on the internet.
Venn Diagrams are NOT similar to the earlier types of diagrams, commonly referred to as Euler Diagrams. They are a revolutionary departure from the earlier diagrams and are incomparably more powerful.
The difference between the earlier diagrams and Venn Diagrams is that the latter show all possible intersections. Those that are empty are shaded or colored distinctively. This contrasts with the earlier diagrams which indicate that an intersection is empty by including no region to which it corresponds. This was correctly pointed out in the latest version of the article, but contradicted elsewhere in the article.
Mathematicians and mathematical writing nearly always make the same mistake as this article, while philosophers and philosophical writing usually give a correct and accurate account.
A correct account can be found in almost any modern introductory philosophy text on logic and critical thinking. (A wrong account can be found in most introductory texts on set theory or logic written by mathematicians.)
Here are some articles on Venn Diagrams. the page at
http://www.combinatorics.org/Surveys/ds5/VennWhatEJC.html
is a general definition
the following comment is key: "Note that some authors refer to diagrams with fewer than 2^n regions as Venn diagrams, but they are more properly termed Euler diagrams, after the mathematician Leonard Euler."
In a Venn diagram all intersections are shown as non empty but are indicated as empty by shading, while in Euler diagrams, emptiness of an intersection is indicated by disjoint interiors (which would disqualify a diagram from being a Venn diagram).
More discussion of Venn Diagrams and the distinction between them and Euler Diagrams can be found in the following sources.
The lower part of the page at
http://www.combinatorics.org/Surveys/ds5/VennOtherEJC.html#euler
shows the comparison correctly. In this article, the notation "AB" means "A intersect B".
This is further explained in the following:
http://www.cut-the-knot.org/LewisCarroll/VennDiagrams.shtml
and
http://www.cut-the-knot.org/LewisCarroll/devlin.shtml
which show how the Venn Diagram is used to solve a syllogism.
The following is by one of the people most to blame for the confusion about what Venn Diagrams really are --- William Dunham. This version of the webpage incorporates the challenge from Frank Ruskey, the author of the Survey of which the pages at the first two urls above are parts. It also includes Dunham's response to the challenge to his misinformation, showing only a cavalier disregard for the educational damage he has inflicted on millions. I definitely recommend reading this to see an example of how the misunderstanding of Venn Diagrams became so widespread.
- So what you're saying is that philosophers and mathematicians differ on how they draw Venn diagrams. Venn was both a philosopher and mathematician, so I'm not sure we can definitively say one method is correct and the other isn't. Is the correct answer the union of both methods? Nerfer (talk) 03:28, 8 January 2021 (UTC)
A Caribbean Venn Diagram to simplify template?
Is there an easy Wikipedia tool to create a Venn Diagram that could allow this folllowing template to be cleaned up? I see what the maker is trying to do but I feel Venn Diagram is the way to go in order to show blocs rather than a Wikipedia template. CaribDigita (talk) 05:35, 22 January 2021 (UTC)
Footnotes
Below are the footnotes from my comment above -- RobLa (talk) 08:33, 23 February 2021 (UTC)
Lead section
The current lead section of Venn diagram says this:
- A Venn diagram, also called primary diagram, set diagram or logic diagram, is a diagram that shows all possible logical relations between a finite collection of different sets. These diagrams depict elements as points in the plane, and sets as regions inside closed curves. A Venn diagram consists of multiple overlapping closed curves, usually circles, each representing a set. The points inside a curve labelled S represent elements of the set S, while points outside the boundary represent elements not in the set S. This lends itself to intuitive visualizations; for example, the set of all elements that are members of both sets S and T, denoted S ∩ T and read "the intersection of S and T", is represented visually by the area of overlap of the regions S and T.[1][2]
- In Venn diagrams, the curves are overlapped in every possible way, showing all possible relations between the sets. They are thus a special case of Euler diagrams, which do not necessarily show all relations. Venn diagrams were conceived around 1880 by John Venn. They are used to teach elementary set theory, as well as illustrate simple set relationships in probability, logic, statistics, linguistics, and computer science.
- A Venn diagram in which the area of each shape is proportional to the number of elements it contains is called an area-proportional (or scaled) Venn diagram.
It seems worth copying the text from "simple:Venn diagram" (at http://simple.wiki.x.io/w/index.php?title=Venn_diagram&oldid=7169930 ) which currently has this text:
A Venn diagram is a diagram that shows the logical relation between sets. They were popularised by John Venn in the 1880s, and are now widely used. They are used to teach elementary set theory, and to illustrate simple set relationships in probability, logic, statistics, linguistics and computer science. A Venn diagram uses closed curves drawn on a plane to represent sets. Very often, these curves are circles or ellipses.
Similar ideas had been proposed before Venn. Christian Weise in 1712 (Nucleus Logicoe Wiesianoe) and Leonhard Euler (Letters to a German Princess) in 1768, for instance, came up with similar ideas. The idea was popularised by Venn in Symbolic Logic, Chapter V "Diagrammatic Representation", 1881.
That seems pretty good. The current enwiki lead should probably be copied into a new "Details" (or "Technical Details") section. Thoughts? -- RobLa (talk) 08:33, 23 February 2021 (UTC)
2002/03 discussion
I drew these using jave.de and I'm aching for the same kind of graphical draw tool as found over at twiki, the twikidraw...I've raised the idea at the village pump... just finding a java person that knows enough about xml to write to the expat library in php...that's all ;) dennisdaniels
I just came looking for the answer to this question - are there sets of sets that cannot be represented by a 2D venn diagram? If so, how about if you extend the diagram to more than 2 dimensions? If somebody knows the answer, it should be included in the article, I think. -- Khendon 10:08 Sep 30, 2002 (UTC)
What's the difference between a Venn diagram and an Euler diagram? The article doesn't even hint at that. Both of the diagrams shown are Venn diagrams, as I have alwasy understood the term. Are they also both Euler diagrams? Michael Hardy 23:57 4 Jul 2003 (UTC)
- They're pretty much the same, except for the name. Mathematicians felt sorry for John Venn, so they named it after him. It's in the article and external link. Poor Yorick 00:04 5 Jul 2003 (UTC)
The page could use some mathematical markup. Like: A is a proper subset of B is written as: A (a rotated U) B, someone know how to make those symbols? BL 19:04, 7 Sep 2003 (UTC)
Anthony Edwards link
I don't think it links to the right Mr. Edwards. T0pem0 11:30, 14 Apr 2004 (UTC)
I am in a Probability Theory class.. and today was like the 3rd day of class. We were talking about Venn Diagrams, and I swear I heard the professor say
"Those are venn diagrams and I encourage you to use them when you think about sex"
So I'm sitting in class, trying to figure out how Venn Diagrams can be applied to sex before I come to the realization that he said "SETS", not sex. Oh well, so much for math being frightfully interesting.
Difference between Venn and Euler diagrams
Contrary to what Poor Yorick writes above, the key difference between Venn and Euler diagrams is this - Venn diagrams explicitly represent the universe of possibilities by enclosing all the circles in a rectangle. This was Venn's key innovation. While it may seem trivial to us, it took mankind 2300 or so years (since Aristotle first wrote about logic) to do this, and it has had a far-reaching consequence: For the first time the complement of a set could be readily represented. Indeed, the graphic at the top of the page does not enclose the three circles in a universe box, and so is NOT a Venn diagram. Someone with better graphic skills than I should fix this diagram to make it a Venn diagram. Peter McBurney, 2006-05-28.
Tools for drawing Venn diagrams
It would appear as if the drawing feature in MS Office (MS Powerpoint) only creates correct Venn diagrams for up to 3 sets. Maybe this is an important distinction among other tools listed?
Diagram Venn.jpg
I created a diagram Venn.jpg; I've contemplated the use of using a rectangle instead of a circle; I like circles. Because it may be a circle, and not a rectangle, would not make it any other diagram than a Venn diagram, however. And I doubt the diagram itself couldn't also be comprised of ellipses, and still be a Venn diagram. Which is my point. They're ellipses. It's not a historic representation of what John Venn himself drew; it is a Venn diagram. But it got deleted. Charles R. Kiss, Sept. 15, 2006
- ^ "Comprehensive List of Set Theory Symbols". Math Vault. 2020-04-11. Retrieved 2020-09-05.
- ^ "Intersection of Sets". web.mnstate.edu. Retrieved 2020-09-05.



