Talk:Pythagorean triple/Archive 5

Archive 1

←

Archive 3

Archive 4

Archive 5

A New Property -- Can Anyone Find it in the Literature?

For primitive PT's: c²+2ab and c²-2ab are both odd squares.

The proof is simple: c²+2ab=a²+b²+2ab=(a+b)². The latter is an odd square because exactly one of a, b is odd. Similarly for c²-2ab.

I don't see this in my copy of Sierpinski's "Pythagorean Triangles"... has anybody seen it somewhere? If so, is it worth adding to "Elementary Properties..."? (And if not, this has to be the most trivial "original research" you can imagine.) CirclePi314 (talk) 09:20, 12 February 2015 (UTC)

This article tends to be a magnet for things that match the description in your final parenthetical. --JBL (talk) 16:29, 12 February 2015 (UTC)

Dubious passage on Platonic sequences

The following was put into the article's section on Platonic sequences on 28 June 2007 by someone who is no longer on Wikipedia:

It can be shown that all Pythagorean triples are derivatives of the basic Platonic sequence (x, y, z) = p, (p² − 1)/2 and (p² + 1)/2 by allowing p to take non-integer rational values. If p is replaced with the rational fraction m/n in the sequence, the 'standard' triple generator 2mn, m² − n² and m² + n² results. It follows that every triple has a corresponding rational p value which can be used to generate a similar triangle (one with the same three angles and with rational sides in the same proportions as the original). For example, the Platonic equivalent of (6, 8, 10) is (3/2; 2, 5/2). The Platonic sequence itself can be derived by following the steps for 'splitting the square' described in Diophantus II.VIII.

This seems wrong to me. First, as far as I can see, the Platonic sequence p, (p² − 1)/2 and (p² + 1)/2 does not give rise to (3/2, 2, 5/2). Second, as far as I can see it is impossible to find any rational p for which this formula gives something that scales to (6, 8, 10). Third, I think the same is true for the different Platonic sequence formula given in the article Diophantus II.VIII.

I conclude from this that in fact the Platonic sequence can generate all primitive triples but not all triples. This feeling is reinforced by the observation in the above passage that the Platonic sequence can be used to derive the 'standard' formula, which generates all primitive triples but which does not generate all triples.

Without objection, I'm going to replace the above passage with the following:

''It can be shown that all primitive Pythagorean triples can be derived from the basic Platonic sequence (x, y, z) = p, (p² − 1)/2 and (p² + 1)/2 by allowing p to take non-integer rational values. If p is replaced with the rational fraction m/n in the sequence, the 'standard' primitive triple generator 2mn, m² − n² and m² + n² results. It follows that every primitive triple has a corresponding rational p value which can be used to generate a similar triangle (one with the same three angles and with rational sides in the same proportions as the original). For example, the Platonic equivalent of (56, 33, 65) is generated by p = m/n = 7/4 as (p, p² –1, p²+1) = (56/32, 33/32, 65/32). The Platonic sequence itself can be derived by following the steps for 'splitting the square' described in Diophantus II.VIII.

Loraof (talk) 17:58, 8 April 2015 (UTC)

I don't understand your objection. If I can make something similar to every primitive triple then I can make something similar to every triple (since every triple is similar to a primitive one). Though the example is confused, since to get the triple (3/2, 2, 5/2) one should put in p = 2 (an integer). --JBL (talk) 18:32, 8 April 2015 (UTC)

Thanks. First, I found (and still find) the phrase "triples are derivatives of ..." confusing. From your comments I can see that this was intended to mean with unrestricted scaling. Second, I was misled by the statement that the Platonic sequence, previously defined as p, (p^2-1)/2, (p^2+1)/2, is exemplified by (3/2, 2, 5/2), which says that p=3/2 and 2=((3/2)^2-1)/2, which is not true. It should be (2, 3/2, 5/2). I'm going to clarify the derivatives wording, and replace the example with one that is correctly sequenced and has a fractional p. Loraof (talk) 19:16, 8 April 2015 (UTC)

Yes, you're certainly right that it was not clearly written at all. Your edit was a big improvement; in a second I will tweak it a bit more. --JBL (talk) 21:30, 8 April 2015 (UTC)

Rightarrow versus implies

In Google Chrome on my laptop running Windows Vista, in the Points on a unit circle section, the \implies produces an arrow which is broken in the middle, but the \Rightarrow looks fine. This may be why the IP 128.84.127.40 changed it. — Anita5192 (talk) 21:14, 29 January 2016 (UTC)

Would it be better just to replace the arrow with the words "and so" or similar? --JBL (talk) 21:20, 29 January 2016 (UTC)

I think it would be equally readable with "and so," or "and," or $\Rightarrow$. I do not understand why $\implies$ looks strange on my computer, or what is wrong with using $\Rightarrow$. I was hoping someone else would see the same problem with $\implies$, and understand why I mentioned this. — Anita5192 (talk) 21:39, 29 January 2016 (UTC)

I also see a funny kink in the symbols \implies and \Longrightarrow. (I am using Firefox on a unix machine.) --JBL (talk) 22:17, 29 January 2016 (UTC)

My general preference in situations like this is to spell it out in words. I think doing it that way makes it less WP:TECHNICAL. —David Eppstein (talk) 23:19, 29 January 2016 (UTC)

Done! Thank you both for your input. I have not heard from D.Lazard, but I hope he approves. — Anita5192 (talk) 02:47, 30 January 2016 (UTC)

Another Property -- Can Anyone Find it in the Literature?

Some triplet comes also from:

$A^{2}=(C+B)/(C-B)$

A=3, B=4, C=5 is the most famous. — Preceding unsigned comment added by 94.81.217.96 (talk) 13:15, 19 May 2016 (UTC)

Well, we know that $A^{2}=C^{2}-B^{2}=(C+B)(C-B)$, so $A^{2}=(C+B)/(C-B)$ if and only if $C-B=\pm 1$. For some Pythagorean triplets it is the case that $C-B=1$, but there are also many Pythagorean triplets for which $C-B\neq \pm 1$. 𝕃eegrc (talk) 14:13, 19 May 2016 (UTC)

Adding link to Boolean Pythagorean triples page

It seems reasonable to add a link to http://en.wiki.x.io/wiki/Boolean_Pythagorean_triples_problem under "See also".

Since I am an author of the article referenced in that page, I don't know whether I should add the link just myself (which seems harmless, since it is another Wikipedia page, and obviously it is related to the current page). Oliver Kullmann (talk) 16:34, 5 June 2016 (UTC)

 Done D.Lazard (talk) 07:52, 6 October 2016 (UTC)

Euclid's formula when a is even

In the text it says that "A proof of the necessity that $a,b,c$ be expressed by Euclid's formula for any primitive Pythagorean triple is as follows". However, Euclid's formula only gives primitive Pythagorean triples with $b$ even. It is for instance obvious that we cannot find m and n such that $m^{2}-n^{2}=4$, $2mn=3$, $m^{2}+n^{2}=5$. As pointed out earlier, if $m-n$ is even and $\gcd(m,n)=1$, Euclid's formula gives $(2a,2b,2c)$ where $(a,b,c)$ is a PPT. For instance $m=3$ and $n=1$ gives $(8,6,10)$.

So a few places, primitive Pythagorean triple should be replaced by primitive Pythagorean triple $(a,b,c)$ where $b$ is even. — Preceding unsigned comment added by HelmerAslaksen (talk • contribs) 19:44, 6 September 2016 (UTC)

Euclid's formula produces the triple (3, 4, 5) with m = 2, n = 1. It also produces every other primitive Pythagorean triple. It also produces a limited family of non-primitive triples, but that is irrelevant to the claim in question. --JBL (talk) 21:06, 6 September 2016 (UTC)

Dear Joel, I'm afraid you didn't understand my post, or we disagree about what we mean by Euclid's formula. My point is that what I call Euclid's formula, $(m^{2}-n^{2},2mn,m^{2}+n^{2})$, will only produce triples $(a,b,c)$ with $b$ even, and not for instance $(4,3,5)$. If you want triples with $b$ odd, you must reorder the formula, or include the values of $m$ and $n$ with $m-n$ even, and then divide by 2. Not sure what you mean by "limited family". Half the time ($m-n$ even) you will get a non-primitive triple.

HelmerAslaksen (talk) 00:34, 6 October 2016 (UTC)

I have fixed this, but it would be better to say (where?) that two triples that differ by the exchange of a and b are considered as equal (because of the commutativity of addition) This was implicitly supposed in the article and is the cause of the confusion. D.Lazard (talk) 07:44, 6 October 2016 (UTC)

The reason why I started this discussion was because I was lecturing about this to a class, and I suddenly realized that it was more difficult that I had first thought. First of all, I believe that we should make our assumptions clear. Otherwise, both we and our students, may suddenly find ourselves getting confused. Secondly, I feel that this explains the $m-n$ condition. The ones with $m-n$ odd are the primitives with $b$ even, and the ones with $m-n$ even are the triples of the form $(2a,2b,2c)$ where $(a,b,c)$ is a primitive triple with $b$ odd. It was only when I saw that, that I felt that I really understood this. — Preceding unsigned comment added by HelmerAslaksen (talk • contribs) 13:28, 6 October 2016 (UTC)

Take a look at Pythagorean triple#Interpretation of parameters in Euclid's formula. There we see that n/m is the lowest terms representation of tan(θ/2) in the Pythagorean triangle where θ is the angle opposite the side of length a. The reason that sometimes we have to divide by two to make the Euclid-generated Pythagorean triple be primitive is that the focus on tan(θ/2) is in some sense inappropriate. If we instead look at tan(θ) = a/b in lowest terms (or look at sin(θ) = a/c or cos(θ) = b/c in lowest terms) we would have two-thirds of our primitive Pythagorean triple immediately, never having to divide by 2. Fortunately, the double-angle formula for a tangent is easy enough to analyze; tan(θ) = 2 tan(θ/2) / (1 - tan²(θ/2)) = 2mn / (m² - n²) will be in lowest terms exactly when n and m are relatively prime and not both odd. If they are relatively prime but both odd then the lowest terms representation for tan(θ) requires that both the numerator 2mn and denominator m² - n² be halved. 𝕃eegrc (talk) 16:29, 6 October 2016 (UTC)

I have added a section "A variant". I have written it in order that both parameterizations of triples (Euclid's and its variant) parameterize the primitive triples with b even. But this could be formulated without exchanging a and b by saying that every primitive triple may be obtained exactly once by choosing m and n coprime and dividing by two if m and n are both odd. D.Lazard (talk) 17:51, 6 October 2016 (UTC)

When m and n are coprime but both odd then (m′, n′) = ((m+n)/2, (m−n)/2) will be coprime, not both odd, and will generate the primitive Pythagorean triple associated with (m, n), but with a and b reversed. This follows, in part, from the fact that the two non-right angles in a Pythagorean triangle sum to π/2, so their half angles sum to π/4, and the formula tan(π/4 - θ/2) = (1 − tan(θ/2)) / (1 + tan(θ/2)). 𝕃eegrc (talk) 15:53, 7 October 2016 (UTC)

a and b are even and odd - not explained properly

There are various parts of the article that assume as a pre-established fact that a is odd and b is even or vice versa. This fact is never established This fact is assumed before it has been established, and is not clearly enough described to justify how much it's referred to. The fact that either a or b is even needs to be made more prominent.

References:

Pythagorean triple/Archive 5#Generating a triple - image to the right:
The primitive Pythagorean triples. The odd leg a is plotted on the horizontal axis, the even leg b on the vertical."

Pythagorean triple/Archive 5#General properties:
The properties of a primitive Pythagorean triple (a, b, c) with a <  b < c (without specifying which of a or b is even and which is odd) include:

• ...
• Exactly one of a, b is odd; c is odd.

Proof (more like a "by the way", I only found it while writing this talk post):

Pythagorean triple/Archive 5#Proof of Euclid's formula: "As a and b are coprime, one is odd, and one may suppose that it is a, by exchanging, if needed, a and b. This implies that b is even and c is odd (if b were odd, c would be even, and c² would be a multiple of 4, while a² + b² would be congruent to 2 modulo 4, as an odd square is congruent to 1 modulo 4)."

--NeatNit (talk) 18:00, 4 May 2017 (UTC)

Primitive triples charted

It would be nice if a chart like this colored triples differently whether they were primitive or not. Tom Ruen (talk) 02:57, 31 August 2017 (UTC)

Pairwise coprime

Since for Pythagorean primitive triples (a,b,c) we have gcd(a,b) = gcd(a,c) = gcd(b,c) = 1. I propose to give this as a property in the article. — Preceding unsigned comment added by 147.215.1.189 (talk) 12:43, 6 October 2015 (UTC)

In the article that is not choosen as a definition, but instead gcd(a,b,c) = 1 : coprime as a set. This not the same! For a ppt one can prove that the above pairwise coprime properties hold. This is done later in the article. I've tried to clear this up. Albert 80.100.243.19 (talk) 20:29, 1 November 2017 (UTC)

Special cases needing references

In the § Special cases section, these three consecutive bullet points need either a simple explanation or references, as appropriate:

• There exist infinitely many Pythagorean triples in which the two legs differ by exactly one. For example, 202 + 212 = 292; these are generated by Euclid's formula when ${\tfrac {m-n}{n}}$ is a convergent to √2.
• For each natural number n, there exist n Pythagorean triples with different hypotenuses and the same area.
• For each natural number n, there exist at least n different Pythagorean triples with the same leg a, where a is some natural number.  Done

yoyo (talk) 13:23, 24 September 2018 (UTC)

The third case is easy, and I have fixed it. The two other involve some results on Diophantine equations, and the proof is probably less elementary. They are probably described in the cited book of Sierpinski, which I have not under hand. D.Lazard (talk) 15:07, 24 September 2018 (UTC)

Vandalism

Pinging @Mifter and Widr: who helped deal with the last disruption: the same person is back with a different IP address. This IP has a more prolific recent history, some of which is similar vandalism. I am not able to check whether the edits to articles about skyscrapers in Taiwan are legitimate. --JBL (talk) 15:43, 2 January 2019 (UTC)

I reported this IP as a sockpuppet and it is now blocked for one day.—Anita5192 (talk) 16:42, 2 January 2019 (UTC)

re paragraph: Fibonacci numbers in Pythagorean triples

Hi! See "the largest number in a Pythagorean triple". For F₉ = 34 this Pythagorean triple is (30, 16, 34) = 2 * (15, 8, 17). So "the largest number in a Pythagorean triple" could be expanded to "the largest number in a Pythagorean triple which must not be a primitive Pythagorean triple".
Regards Gangleri 11:56, 9 July 2019 (UTC) — Preceding unsigned comment added by 217.86.249.144 (talk)

The definition of a Pythagorean triple is given in the lead, and it is clear that a Pythagorean triple may be primitive or non-primitive. In this section, this is "Pythagorean triple", not "primitive Pythagorean triple" that is used. I do not see the need of recalling here the clear definitions of the lead. Also your suggestion of expansion is ambiguous and confusing, as "not" may refer to either "must" or "be", and this gives two contradictory meanings to your sentence. A correct version of your suggested addition would be "... which may be primitive or not". Again, this does not add anything useful to the article. D.Lazard (talk) 13:20, 9 July 2019 (UTC)

Generating Pythagorean Triples

It may be true that what follows has been published, but, if so, I haven't seen it. (Or, because I'm either (a) too lazy or (b) too innumerate to decipher all of the article about Pythagorean Triples, it may be described in that article.) Using an Excel spreadsheet and some tinkering with known primitive triples, I came up with the following four series or formulas for developing Pythagorean Triples.

Formulas for creating Pythagorean Triples

1. Let "n" be a counting number. Side a = 2n+1, which yields an odd number, beginning with 3. Side b = (2n+1)^2/2 - 0.5 Side c = (2n+1)^2/2 - 0.5 This will produce the familiar list {3,4,5},{5,12,13},{7,24,25}, and so on. All triples made this way will be primitive.
2. Let "n" be a counting number. Side a = 4n+4, which yields a multiple of 4, starting with 8. Side b = 4(n + 1)^2 - 1 Side 3 = 4(n + 1)^2 + 1 This produces the list {8,15,17},{12,35,37},{16,63,65}, and so on. All triples made this way will be primitive.
3. Let "n" be a counting number. Side a = 8n+12, which yields a multiple of 4 starting with 20. Side b = (2n+3)^2 - 4 Side c = (2n +3)^2 + 4 This produces the list {20,21,29},{28,45,53},{36,77,85}, and so on. All triples made this way will be primitive.
4. The fourth set of formulas yields some primitive triples already contained within one of the formulas above, or is a multiple of those found in the first formula. However, there are other primitive triples which are not found in any of the three formulas above. {15,8,17},{21,20,29},{27,36,45} are the first three in this series. The first two are found in formulas 2 and 3, respectively, and the third is 9 times the first triple found in formula #1. However, the fourth triple in this new series is {33,56,65}, which not only is primitive, but is not found within any of the other three formulas. Side a = 6n + 9 Side b = 2n^2 + 6n Side c = 2n^2 + 6n + 9 Every third triple is nine times the next triple found in the formula #1 above, and the remaining triples are all primitive, and are not contained within any of the first three formulas.

If there is another formula for deriving Pythagorean Triples other than the four above, I do not know it. The most common way to derive a P.T. as stated in most math textbooks is to choose two different counting numbers m and n, then apply the following expressions to obtain the three side lengths: |m^2-n^2| , 2mn, and m^2 + n^2. My gut feeling, not proven, is that no matter what two numbers are chosen, the resulting P.T. will be found in one of the four series described above. Also, it appears that, if the difference between m and n is odd, the triple formed will be primitive.

72.243.144.96 (talk) 02:57, 10 July 2019 (UTC) Tom Hobbs

Your four series are the special case of the general formula |m^2-n^2| , 2mn, and m^2 + n^2 with $(m,n)$ equal respectively to $(k+1,k),$ $(2k+2,1),$ $(2k+3,2),$ $(k+3,k).$ Your conjecture is wrong: one has a triple that is not in any of your series by taking $(m,n)$ with $2<n<m-3.$ D.Lazard (talk) 09:01, 10 July 2019 (UTC)

Semi-protected edit request on 17 July 2019

Please vikify the first ocurence of hypotenuse. Thanks in advance no bias — קיין ומוויסנדיק פּרעפֿערענצן — keyn umvisndik preferentsn ^{talk contributions} 18:51, 17 July 2019 (UTC)

I have linked the first occurrence of hypotenuse, if that is what you meant by "wikify."—Anita5192 (talk) 18:58, 17 July 2019 (UTC)

unique properties

Berggrens's tree using the unique vales (m, n), (u, v) and (b, n) associated with the primitive Pythagorean triples these values generate

Hi! I think the article should emphasize the unique properties of the primitive Pythagorean triple(t)s. What I try to tell: "Exactly one of a, b is divisible by 3." (3, 4, 7) has this property too but it is not a Pythagorean triplet. regards no bias — קיין אומוויסנדיק פּרעפֿערענצן — keyn umvisndik preferentsn ^{talk contribs} 02:12, 19 July 2019 (UTC)

"Reciprocal" or "upside-down" Pythagorean theorem

Titus III has recently made an addition (once, twice) concerning the "upside-down Pythagorean theorem". The obvious problem with it is that it refers to the equation ${\frac {1}{x^{2}}}+{\frac {1}{y^{2}}}={\frac {1}{z^{2}}}$ as a theorem, and this is obviously wrong: it's missing all the associated data (what do those symbols x, y, z represent?) that one needs to make sense of it. I think inclusion in some form is possible; in accordance with WP:BRD, I propose we discuss here to refine it first. --JBL (talk) 18:41, 16 August 2019 (UTC)

Thanks, Joel B. Lewis. The variables $x,y,z$ are explained in Alexander Bogomolny's https://www.cut-the-knot.org/pythagoras/PTForReciprocals.shtml. Given a right triangle, $x,y$ are the legs and $z$ is a line perpendicular to the hypotenuse that intersects the common vertex of the legs. A nice diagram is included in Bogomolny's link. Titus III (talk) 18:49, 16 August 2019 (UTC)

To Joel B. Lewis, I propose the following REVISED edit explaining the variables,

"The upside down Pythagorean theorem,

${\frac {1}{x^{2}}}+{\frac {1}{y^{2}}}={\frac {1}{z^{2}}}$

gives the relationship of the two legs $x,y$ of a right triangle to the altitude $z$ (a line from the right angle and perpendicular to the hypotenuse). The equation can be transformed to,

${\frac {1}{(ac)^{2}}}+{\frac {1}{(bc)^{2}}}={\frac {1}{(ab)^{2}}}$

and $a,b,c$ is the Pythagorean triple $a^{2}+b^{2}=c^{2}$. If the $x,y,z$ are to be integers, the smallest solution $x>y>z$ is then

${\frac {1}{20^{2}}}+{\frac {1}{15^{2}}}={\frac {1}{12^{2}}}$

using the smallest Pythagorean triple $3,4,5$." Titus III (talk) 19:14, 16 August 2019 (UTC)

I oppose to the inclusion of this section. This contains two things. Firstly a geometrical interpretation, called "Pythagorean theorem for reciprocals" or "upside-down Pythagorean theorem", of the solutions of the equation $\textstyle {\frac {1}{x^{2}}}+{\frac {1}{y^{2}}}={\frac {1}{z^{2}}}.$ This is misplaced here, as (if it is notable enough for inclusion in WP) its place should be in Pythagorean theorem. The second part of the section is to suggest calling "primitive upside-down Pythagorean triple" a solution such that $x,y,z$ are integers without common divisors. It is easy to prove that $x,y,z$ is a primitive upside-down Pythagorean triple if and only if there exist a primitive Pythagorean triple $a,b,c$ such that $x=ac,y=bc,z=ab.$ The proof is an exercise for students learning properties of greatest common divisors. As this property seems to not have any other use than such an exercise, and as Wikipedia is not a repository for student exercises, I oppose to add this result to the article. D.Lazard (talk) 20:10, 16 August 2019 (UTC)

To D.Lazard, Your original comment in the main article contained two points. Your said it, "Refers to a theorem that is not stated. Moreover, this new section is based on a single primary source." The revised edit addresses those two points: 1st, the theorem is now stated with the variables $x,y,z$ explained and is certainly notable as it surprisingly relates the legs $x,y$ not with the hypotenuse but with the ALTITUDE $z$. This answers your and Joel B. Lewis's question about the nature of $x,y,z$. 2nd, more distinct sources and authors are given. Many more can be given if so desired, and which shows this has an established literature behind it as required by Wk. Your new comment about "primitivity" is irrelevant, as the revised edit makes no mention about primitivity nor considers it important. Titus III (talk) 03:15, 17 August 2019 (UTC)

I hadn't realized what article we were on; I agree with D.Lazard that this content belongs in Pythagorean theorem, not in Pythagorean triple. --JBL (talk) 10:41, 17 August 2019 (UTC)

Joel, very well, I will transfer it to the article Pythagorean theorem. The important thing is that the very notable relationship between four line segments of a right triangle namely $a,b,c$ and altitude $h$ where $\textstyle a^{2}+b^{2}=c^{2}$ and $\textstyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{h^{2}}}$ appears in Wikipedia.Titus III (talk) 11:29, 17 August 2019 (UTC)

Joel B. Lewis, it is now in Pythagorean theorem. I've also added connections to the optic equation and heptagonal triangles. Titus III (talk) 02:25, 18 August 2019 (UTC)

References

Misleading "property"

Quoting the section on properties: "For each natural number n, there exist at least n different Pythagorean triples with the same hypotenuse.[8]:31"

It is not clear what is meant by this. I interpreted it as "with n as hypotenuse", which is clearly wrong (There is only one triplet with 5 as hypotenuse: (3,4,5)). Otherwise, what is that "same hypotenuse"? Is this just a difficult way of stating that there exist inifinitely many Pythagorean triples?37.44.138.159 (talk) 10:53, 9 September 2019 (UTC)

This means that for every n, there exists c such that there are at least n different triples of the form $a^{2}+b^{2}=c^{2}.$ D.Lazard (talk) 11:15, 9 September 2019 (UTC)

historic doubtful

I read the pragraphe of "historic . It s a shame that in an scientfic article , you mix some semitic revendications nationalist and fascist If i read the article about "plimpton 322" there are some tones of theories and nobody agrees how to translate this babylonian document . Some theories tell t that the document was a table of reciprocal numbers , some other tell it was trigonometry , some other , it was a commercial transation document . Is it serious ? Which one is the good ?

So why should it be marked i as historic in this page ? Tio make please to fascists ? In addition , why this historic doesn t make mention about all the other dicoveries in the history about pythagorician triplets ? Is it shameful for semitics ? Miranda2016 (talk) 15:46, 16 January 2020 (UTC)

I'm sorry, but this is impossible to decipher. --JBL (talk) 17:34, 16 January 2020 (UTC)

why switch from k to s?

k in the lede for "if (abc) is a triple, then so is (ka kb kc) but s in the diagram. --142.163.195.153 (talk) 16:55, 25 February 2021 (UTC)

Well, variables don't care what name you call them by, but I've changed it to make it consistent. --JBL (talk) 17:34, 25 February 2021 (UTC)

Need citation for n-tuple stereographic projection

Thank you @DVdm: for looking out for encyclopedic concerns. All, if you have a citation that backs the following, please supply it here.

====n-tuple stereographic projection====

Stereographic projection of the unit circle onto the hyperplane orthogonal to the N axis. Given a point P on the unit hypersphere, draw a line from P to the point N = (0, ..., 0, 1). The point P′ where the line intersects the hyperplane is the stereographic projection of P.

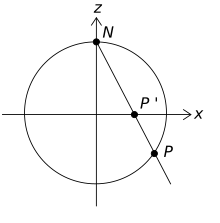
Much as a primitive Pythagorean triple a² + b² = c² can be identified with the point (a/c, b/c) that has rational coordinates and lies on the unit circle, a primitive Pythagorean n-tuple a₁² + ... + a_n−1² = a_n² can be identified with the point (a₁/a_n, ..., a_n−1/a_n) with rational coordinates on the unit hypersphere with n−2 dimensions. Furthermore, stereographic projection defines a one-to-one relationship between points on this hypersphere that have rational coordinates and points on a hyperplane with the same number of dimensions that have rational coordinates. In this case, a point P = (r₁, ..., r_n−2, r_n−1) on the unit hypersphere with rational coordinates is mapped by a projection from N = (0, ..., 0, 1) to a point

$$P'=\left({\frac {r_{1}}{1-r_{n-1}}},\ldots ,{\frac {r_{n-2}}{1-r_{n-1}}},0\right)$$

that is on the hyperplane spanned by all but the last dimension. Unwinding this process, any point P′ with rational coordinates on the hyperplane gives a unique primitive Pythagorean n-tuple.

Thank you —Quantling (talk | contribs) 18:57, 23 March 2021 (UTC)

Calling out again for anyone who can provide a citation for this; that would be the best way to keep things encyclopedic.

Barring that, is there a case that this is obvious under the WP:CALC criteria? I've read a lot of textbooks but don't always remember where I have seen things. Under the assumption that I am not that smart, whatever I remember is going to be at most a trivial extension of what I have read. If you think that the suggested text above is pretty obvious given your math background please speak up. If there enough who feel this way, maybe we have a case for WP:CALC. For example, the section in this very same article about stereographic projection of (non-tuple) Pythagorean triples has no citation. (But much better would be if anyone has an actual citation. Please don't be shy!) Thank you —Quantling (talk | contribs) 13:53, 3 April 2021 (UTC)

Lead problems

From WP:LEAD "Apart from basic facts, significant information should not appear in the lead if it is not covered in the remainder of the article." Right now, the lead contains an extended definition that does not exist in the article body. I just tried to remedy this but was reverted. I invite suggestions and how to fix this. LK (talk) 06:36, 9 April 2021 (UTC)

The definitions of Pythagorean triples and primitive Pythagorean triples are basic facts. So, there is nothing to remedy, since your quotation of WP:LEAD begins with "Apart from basic facts". D.Lazard (talk) 09:42, 9 April 2021 (UTC)

That's not what that means. Basic facts here mean items like birth dates and nationality, or the writing of the term in the original language. Not the extended definition that currently resides in the lead. See for example, the GA Hilbert space, which has a 'definition' section. LK (talk) 02:36, 12 April 2021 (UTC)