Talk:Lemniscate elliptic functions

Lemniscate constant

The article Lemniscate constant redirects here, yet there's no mention of lemniscate constant. Not very helpful when you read about squircle where lemniscate constant is mentioned, but when you follow the link you come here and remain clueless. -- Heimdall 11:58, 28 January 2016 (UTC)

Retargetted the redirect to a better link target.

--Matthiaspaul (talk) 03:52, 1 August 2017 (UTC)

It redirects to here again, but hopefully the description is now a bit more useful. –jacobolus (t) 01:53, 22 August 2021 (UTC)

MOS:VAR

Hi A1E6,

Sorry, I’m not trying to step on your toes here. I want to substantially expand / clarify this article: add a bunch more diagrams and maybe some animations, add a section about the history, add some discussion of practical applications, add diagrams and more explanation of the relationship to elliptic integrals and to Weierstrass/Jacobi or other elliptic functions with the same lattice, add citations to whatever books/papers I can track down, etc.; trying to make the LaTeX formulas fit in a more compact space by using inline fractions, aligning equations, etc. was just a convenient first place to dip in.

I think skipping parentheses around arguments such as $\operatorname {arcsl} r$ vs. $\operatorname {arcsl} (r)$ slightly reduces visual clutter, is consistent with Wikipedia articles about trigonometric functions, and is generally not ambiguous. And similarly for other changes. But if you feel strongly about that or other stylistic choices, I’m happy to discuss it / switch some stylistic choices back. I’m not trying to mangle your work.

I changed a few variable names, again in the interest of clarity (trying for standardish symbols, avoiding overloading symbols for different uses where possible, and so on).

I still don’t feel like I have a full handle on the more advanced number theory etc. topics relevant here, but I’m trying to learn what I can, and .

If I can get some nice diagrams working in this page and at the Dixon elliptic functions page, I might try later to make some improvements of the pages about the Weierstrass ℘ function, the Jacobi elliptic functions, maybe the complex argument sections of the trigonometric pages, etc.

But anyway, I’m more than happy to defer to your choices if you feel strongly, or try to come to some consensus about what is most legible/etc.

–jacobolus (t) 01:35, 17 August 2021 (UTC)

Hi Jacobolus,

I wasn't quite satisfied with several edits, for example changing $\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}x+\operatorname {sl} ^{2}x\operatorname {cl} ^{2}x=1$ to $1=\operatorname {sl} ^{2}x+\operatorname {cl} ^{2}x+\operatorname {sl} ^{2}x\operatorname {cl} ^{2}x$; it's just weird-looking and non-standard like $1=\sin ^{2}x+\cos ^{2}x$. And for example, changing $\operatorname {sl} {\tfrac {\varpi }{2}}$ to $\operatorname {sl} {\tfrac {1}{2}}\varpi$. Also I think that ${\tfrac {1}{2}}{\frac {c_{n}}{a_{n}}}$ is just worse than ${\frac {1}{2}}{\frac {c_{n}}{a_{n}}}$ – the fractions are inconsistent in size (see the "Methods of computation" subsection). The edits mentioned above do not reflect your edits exactly, but I think they convey relevant information.

Other than that, you obviously work hard on improving this article and I appreciate that, especially the diagrams and finding references.

However, I think this article is missing something – the complex plot of $\operatorname {sl}$ or $\operatorname {cl}$, with domain coloring (I think it is even more important than the real plots in the case of elliptic functions), showing the minimal periods $(1+i)\varpi$ and $(1-i)\varpi$. If you can make it, that will be great :) A1E6 (talk) 10:59, 22 August 2021 (UTC)

Yes, I intend to add complex phase portraits (like Wegert’s), but making them is more difficult and time consuming than making the real-valued plots with Desmos; I made a fast enough function approximation (https://observablehq.com/@jrus/fast-peirce-quincuncial) but I need to go track down my code for rendering phase portraits; it’ll take a couple hours of time, and I have been procrastinating from doing that, because lots of other things can be done in small bits here and there.

Inre the small inline-style fractions: there are some cases where a full-sized fraction is probably better, but for places like Lemniscate elliptic functions#Specific values it makes the whole list a lot more compact. I was in other projects working with a lot of half-angle sines and tangents, and writing $\tan {\tfrac {1}{2}}(a+b)$ is a lot nicer than $\tan {\frac {a+b}{2}}$ as well as more clearly indicating that $x\mapsto \tan {\tfrac {1}{2}}x$ should often be thought of as the relevant function (i.e. one stereographic projection step rather than 2 separate steps of dividing by two and then taking a tangent). You can see how e.g. the notation of Gauss and Salzer is clearer than Henrici or Baltensperger or Bandiziol, based on the use of the separate inline half, https://observablehq.com/@jrus/eventrig.

–jacobolus (t) 22:26, 22 August 2021 (UTC)

Inre the methods of computation section, I find this very hard to read:

$\theta _{1}(x;q)=\sum _{n\in \mathbb {Z} }q^{(n+1/2)^{2}}e^{(2n+1)ix+(n-1/2)i\pi }=2\sum _{n=0}^{\infty }(-1)^{n}q^{(n+1/2)^{2}}\sin((2n+1)x),$

Is there a way we can clarify it? e.g. it might help to use $\exp(x)$ rather than $e^{x}$ –jacobolus (t) 22:29, 22 August 2021 (UTC)

What about $\tan {\tfrac {x}{2}}$ (note that \tfrac was used)? I think it is "saving more space" than $\tan {\tfrac {1}{2}}x$.

You can rewrite $e^{\text{stuff}}$ as $\exp {\text{stuff}}$ if you will. A1E6 (talk) 23:13, 22 August 2021 (UTC)

I often use the small fraction just for half because it makes the other symbol stay full-sized, and those can be easier to read. I prefer consistent use of $\tan {\tfrac {1}{2}}x$ to $\tan {\tfrac {x}{2}}$ (and e.g. $\tan {\tfrac {1}{2}}{\bigl (}\theta +{\tfrac {1}{2}}\pi {\bigr )}$ vs. $\tan {\tfrac {2\theta +\pi }{4}}$ or $\tan \left({\frac {\theta }{2}}+{\frac {\pi }{4}}\right)$ etc.). But if you have some equations you want to put back how they were or otherwise tweak in a way you think is more legible, please have at it; my preferences aren’t any kind of gospel. –jacobolus (t) 23:23, 22 August 2021 (UTC)

Are you going to change every $e^{\text{stuff}}$ to $\exp {\text{stuff}}$? The current version is inconsistent. A1E6 (talk) 22:04, 26 August 2021 (UTC)

Lemniscatic / pseudolemniscatic case of Weierstrass function

Should this article actually start with the "pseudolemniscatic" case of the Weierstrass function? Seems like it more properly aligns with the lattice of the lemniscate functions. https://personal.math.ubc.ca/~cbm/aands/page_662.htm

–jacobolus (t) 17:50, 18 August 2021 (UTC)

Dummy variables

(Copied from User talk:Jacobolus#Dummy variables)

Hi, Jacobolus.

In the lemniscate elliptic functions article, I noticed that you wrote expressions like

$\int _{x}^{1}{\frac {x^{2}\mathop {\mathrm {d} x} }{\sqrt {1-x^{4}}}}.$

Mathematicians generally discourage others from using this "notation". It is akin to (for example)

$\sum _{n=1}^{n}{\frac {1}{n}}.$

Please consider changing it to (for example)

$\int _{x}^{1}{\frac {t^{2}\mathop {\mathrm {d} t} }{\sqrt {1-t^{4}}}}.$

I would have edited the page myself but you use this notation in the accompanying diagram as well. A1E6 (talk) 23:57, 28 August 2021 (UTC)

Hi A1E6. I can try to switch to using a dummy variable, for consistency with the rest of the article. The notation with variable name re-used seems very common in the literature I have seen about lemniscate functions, Dixon functions, etc. (written by mathematicians of one kind or another). I think the idea is that when the variable represents a concrete geometric quantity, it can make equations easier to relate to diagrams, avoiding confusion. But it’s probably also fine with a dummy variable. –jacobolus (t) 01:30, 29 August 2021 (UTC)

fourth root of cube in integral formulas

I'm curious about the integral formulas like e.g.

$\int {\frac {1}{\sqrt[{4}]{(x^{4}+1)^{3}}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {x}{\sqrt[{4}]{x^{4}+1}}}\right)}$

It seems to me this would be clearer written as:

$\int {\frac {1}{(x^{4}+1)^{3/4}}}\,\mathrm {d} x={\operatorname {arcsl} }{\left({\frac {x}{\sqrt[{4}]{x^{4}+1}}}\right)}$

But maybe the order of cubing and then 4th root is intentionally separated? For complex values I suppose this might result in different branch cuts, under standard definitions? Though it’s not clear to me which versions will actually yield results matching the right-hand side of the equation for all complex values. (I guess I should make some implementations of these functions and test empirically.)

Also, is there a published source for any of these formulas? –jacobolus (t) 07:05, 30 August 2021 (UTC)

I don't know whether there's a published source. The discussion about different branch cuts doesn't matter IMO, as there's no range of validity specified anyway (but it should be at least some open subset of the reals). Also, as far as I can tell from my experience, not specifying the range of validity is unfortunately a rather common practice on English Wikipedia.

Anyway, I think the current root notation is fine. But feel free to change that. A1E6 (talk) 09:03, 30 August 2021 (UTC)

Maybe check some integral tables where the result could be written in terms of the incomplete elliptic integral of the first kind, i.e. $\operatorname {arcsl} x=\operatorname {F} (\arcsin x,i)$. A1E6 (talk) 12:25, 30 August 2021 (UTC)

re-organization, mixing sl/cl and slh/clh

I'm tempted to reorganize the article to promote 2nd level sections to top level, and put parallel discussions about the sl/cl and slh/clh functions into every section where they are relevant.

Since these functions are so closely related in the complex plane, I think this could help readers see the parallels and slightly better understand each in the context of the other. (Still is going to require some solid pictures showing behavior in the complex plane.)

What do other people think?

–jacobolus (t) 07:28, 30 August 2021 (UTC)

I think sl/cl and slh/clh should be separated, given that there are separate articles for trigonometric and hyperbolic functions. sl/cl and slh/clh are at least not in the same section here. A1E6 (talk) 09:09, 30 August 2021 (UTC)

But there are already places where the lemniscate is together with the circle. Maybe mixing sl/cl with slh/clh and showing analogy is not a bad idea after all. A1E6 (talk) 12:10, 30 August 2021 (UTC)

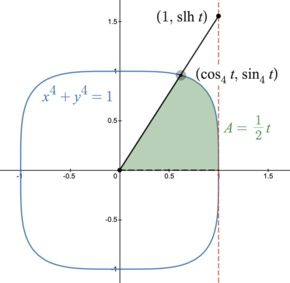
We can make an analogous picture for $x^{4}-y^{4}=1$ and the sl function

I want to add a section showing how shl and sl are the analog of the tangent function with respect to the quartic sine/cosine and hyperbolic quartic sine/cosine, respectively (these are the functions from an area of a "sector" from the origin to the coordinates on the curve $x^{4}+y^{4}=1$ or $x^{4}-y^{4}=1$). So we could write e.g. $\operatorname {sl} z=\tanh _{4}z={\frac {\sinh _{4}z}{\cosh _{4}z}}$, $\operatorname {slh} z=\tan _{4}z={\frac {\sin _{4}z}{\cos _{4}z}}$. The quartic sines/cosines are not themselves elliptic functions, but their squares and ratio are. For the general $x^{n}+y^{n}=1$ case see Grammel (1948) “Eine Verallgemeinerung der Kreis-und Hyperbelfunktionen” https://doi.org/10.1007/BF02038206. And more generally Gambini & al. (2021) “Keplerian trigonometry” https://doi.org/10.1007/s00605-021-01512-0. The cubic analogs are the Dixon elliptic functions.

After the section(s) about symmetries of the lemniscate and hyperbolic lemniscate functions it would be nice to compare them directly, showing how they are complex-rotated variants of the same functions.

Then I want to put the material about Weierstrass/Jacobi functions into a new section comparing various elliptic (and other) functions on to the lemniscatic / pseudolemniscatic lattices.

–jacobolus (t) 18:13, 30 August 2021 (UTC)

Sounds good :) A1E6 (talk) 18:39, 30 August 2021 (UTC)

@Jacobolus: I got the idea that mixing sl with slh everywhere might be criticized by someone, as the hyperbolic variants seem to be far less notable/important (maybe you're creating the complex diagrams right now). A1E6 (talk) 18:49, 30 December 2021 (UTC)

Schwarz–Christoffel map vs conformal map

Regarding "the Schwarz–Christoffel map from the complex unit disk" and "This map was the first ever picture of a Schwarz-Christoffel mapping, in Schwarz (1869)": Shwarz–Christoffel maps map the whole upper half plane onto a certain subset of $\mathbb {C}$, but the unit disk is partially not even in the upper half plane. I think "Shwarz–Christoffel map" should be changed to the more general "conformal map". A1E6 (talk) 16:32, 5 September 2021 (UTC)

The Wikipedia article’s definition of Schwarz–Christoffel transformations is misleading. Maps from the disk to a polygon are also considered Schwarz–Christoffel transformations by most sources (including, notably for this case, Schwarz’s paper which was one of the two introducing the concept). –jacobolus (t) 20:01, 5 September 2021 (UTC)

The two are more or less interchangeable, as you can get from the disk <-> the half plane by a Möbius transformation. At some point I’ll try to rewrite the Schwarz-Christoffel map article, add a bunch more sources, etc. You might enjoy this project of mine from last year: SCPie. Some sources even consider maps to a polygon from an infinite strip or rectangle to fit in the category of Schwarz–Christoffel maps, though that’s probably a bit more controversial as a definition. –jacobolus (t) 20:05, 5 September 2021 (UTC)

"At some point I’ll try to rewrite the Schwarz-Christoffel map article" That's great, but I think "conformal map" should be mentioned in the meantime instead, so that readers who click the link are not confused. A1E6 (talk) 20:17, 5 September 2021 (UTC)

A Schwarz–Christoffel map is a specific type of conformal map. I can go amend the SC Map article right now though. –jacobolus (t) 20:38, 5 September 2021 (UTC)

According to the current Wikipedia definition, SC implies conformal but conformal does not necessarily imply SC. Either the definition of SC on Wikipedia should be changed, or the Lemniscate elliptic functions article should be changed. A1E6 (talk) 20:48, 5 September 2021 (UTC)

I see you've already changed the SC article. But I think you should include some English sources in favor of the unit disk definition. I managed to find some SC sources but all of them use strictly the upper half plane definition. A1E6 (talk) 21:41, 5 September 2021 (UTC)

Christoffel (1867) uses maps from the half plane. But Schwarz (1869) includes the exact case relevant here, of the map from disk <-> square. It’s a simple change of variables to go from one to the other (and the resulting formula is the same for both cases, but with prevertices on the unit circle instead of the real line), and many (most?) sources discuss them both together. But here’s an example https://link.springer.com/content/pdf/10.1007/BF02259911.pdf –jacobolus (t) 06:44, 6 September 2021 (UTC)

Oh weird; that link (from google?) went to a PDF for me, but now only shows a paywall. Well, the Trefethen & Driscoll book Schwarz–Christoffel Mapping makes a good example then, or here’s Trefethen’s first paper about the topic https://apps.dtic.mil/sti/pdfs/ADA068210.pdf or Trefethen & Driscoll’s review paper http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.33.1596&rep=rep1&type=pdf. Or try Nehari’s book Conformal Mapping (chapter 5, section 6), or Henrici’s book Applied and Computational Complex Analysis I (Theorem 5.12e, p. 406). –jacobolus (t) 06:53, 6 September 2021 (UTC)

Thank you for providing the sources :) A1E6 (talk) 13:20, 6 September 2021 (UTC)

More Specific Field

Is there a more specific field that could describe these functions to use in the lead? Instead of just "in mathematics" maybe in "analytic geometry" or whatever the appropriate field(s) are.Arecaceæ2011 (talk) 10:05, 8 October 2021 (UTC)

Use of first person

I've removed every instance of the mathematical 'we' and will now remove that maintenance template. Feel free to check that all the discussion of the math does not have any errors after my edits; I did not change any of the math itself. Arecaceæ2011 (talk) 10:24, 8 October 2021 (UTC)

Seems fine. Though note MOS:WE says: "some such forms are acceptable in certain figurative uses. For example: [...] The author's we found in scientific writing, though rephrasing to use passive voice may be preferable". –jacobolus (t) 16:12, 8 October 2021 (UTC)

Product and sum identities - reference

Can anyone provide a reference for the sum and product identities, presented after "Two other fast computation methods use the following sum and product series:"? For the product formulae I managed to find an online resource on a personal blog-type page: "A collection of Infinite Products and Series" (Andreas Dieckmann), at the url: http://www-elsa.physik.uni-bonn.de/~dieckman/InfProd/InfProd.html (accessed on 12 Oct 2021). (The page is long - search for "Product approximations".) But no derivation is given there. — Preceding unsigned comment added by Mattmajic (talk • contribs) 04:17, 12 October 2021 (UTC)

Regarding the product identities, the first one follows from [1], [2] and [3]. A1E6 (talk) 10:23, 12 October 2021 (UTC)

Relevance of periods in "Methods of computation"

Context: the question is, in a "methods of computation" section, what kind of information should be included about the background/basis of the methods in question. Specifically, this bit: Several methods of computing $\operatorname {sl} x$ involve first making the change of variables $\pi x=\varpi {\tilde {x}}$ to scale the input so the function has real period $2\pi$ instead of $2\varpi ,$ and then computing $\operatorname {sl} \left(\varpi {\tilde {x}}/\pi \right).$ –jacobolus (t) 17:14, 30 October 2021 (UTC)

(copying this from user talk:jacobolus)

I meant "irrelevant" in the context of computation which is what that section is about (regardless of how the formulas were arrived at). We could list all the stuff used to prove the formulas, but that really doesn't belong in that section.

This brings me to the Landen transformations algorithm... But Landen transformations are the key element of it and "deserve" to be mentioned. However, in the case of other computation methods, stuff other than the periods is "in the background" as well, such as the location of the roots and poles. A1E6 (talk) 11:04, 30 October 2021 (UTC)

I added that bit of text because I rewrote the equations afterward explicitly in terms of the changed variable $\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=\dots$ because the formulas end up simpler and less cluttered that way than when putting the change of variables on the right-hand side and writing down formulas for $\operatorname {sl} \left(x\right)=\dots$ fully expanded. But I expect readers might be mystified by the reason for that. Explaining that this change of variables aligns the period of the lemniscate functions with the period of the trigonometric functions by which they are being approximated hopefully clears up any confusion. I dunno... does that seem like a reasonable approach? We could of course leave the original formulas for $\operatorname {sl} \left(x\right)=\dots$ instead, I just thought they were harder to follow. –jacobolus (t) 17:14, 30 October 2021 (UTC)

Well, I didn't say there was anything wrong with rewriting the left-hand sides as $\operatorname {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}$. I found only this part problematic: "so the function has real period $2\pi$ instead of $2\varpi ,$". But other things than periods are at play, for example the location of the roots and the poles. It doesn't make sense to me to mention just the periods as if they were "superior" in proving the formula.

In other words, one could argue that "no, the reason is that the roots are aligned with the roots of $\sin$..." (or something else). I think it is pointless; really, there are many things at play, so I would like the problematic text to be removed.

Don't expect readers might be "mystified". For example,

$\mathrm {sl} (x)=2\exp \left(-{\tfrac {1}{4}}\pi \right)\sin \left(x/G\right)\prod _{n=1}^{\infty }{\frac {1-2\cos \left(2x/G\right)\exp \left(-2n\pi \right)+\exp \left(-4n\pi \right)}{1+2\cos \left(2x/G\right)\exp \left[-\left(2n-1\right)\pi \right]+\exp \left[-(4n-2)\pi \right]}}$

was rewritten as

$\mathrm {sl} {\Bigl (}{\frac {\varpi }{\pi }}x{\Bigr )}=2\exp {\bigl (}{-{\tfrac {1}{4}}\pi }{\bigr )}\sin(x)\prod _{n=1}^{\infty }{\frac {1-2\cos \left(2x\right)\exp \left(-2n\pi \right)+\exp \left(-4n\pi \right)}{1+2\cos \left(2x\right)\exp \left[-\left(2n-1\right)\pi \right]+\exp \left[-\left(4n-2\right)\pi \right]}}$

simply because it reduces clutter; that's it. A1E6 (talk) 17:37, 30 October 2021 (UTC)

I still want to reorganize this article to put sl/cl and slh/clh in parallel in most sections (have gotten distracted by other things), and think it would then be great to put this 'computation' section at top level (somewhere near the end of the article) and elaborate about why these methods work, where they put poles, and so on. If there is enough material it could be broken into sub-sections talking about specific approaches. The more a list of formulas can be contextualized and explained, the better they fit into an encyclopedia article. –jacobolus (t) 19:07, 30 October 2021 (UTC)

You're right; perhaps the background should be included. But still, mentioning only the periods is not the right way. A1E6 (talk) 20:57, 30 October 2021 (UTC)

As an aside, do you know what the region of convergence is for these approximations? How far away from the real line are they effective? –jacobolus (t) 18:51, 30 October 2021 (UTC)

The above formulas are valid everywhere in $\mathbb {C}$. A1E6 (talk) 20:20, 30 October 2021 (UTC)

Aside #2: this paper has some nice explanation and context, linking to various applications of the lemniscate functions, and provides a polynomial-based approximation which should be very fast to compute. Boyd (2011). "New series for the cosine lemniscate function and the polynomialization of the lemniscate integral". Journal of Computational and Applied Mathematics. 235 (8). doi:10.1016/j.cam.2010.09.020. –jacobolus (t) 19:43, 30 October 2021 (UTC)

Boyd says there that some context about the general concept of "imbricate" series can be found in Boyd (1989). "New directions in solitons and nonlinear periodic waves: polycnoidal waves, imbricated solitons, weakly nonlocal solitary waves, and numerical boundary value algorithms". Advances in applied mechanics. 27: 1–82. doi:10.1016/S0065-2156(08)70194-7. –jacobolus (t) 21:02, 30 October 2021 (UTC)

http://dlmf.nist.gov/22.12 might be of use as well. A1E6 (talk) 21:08, 30 October 2021 (UTC)

Minimal periods in the complex plane

(copied from user talk:jacobolus)

The concept of minimal periods in the complex plane is not defined anywhere on Wikipedia as far as I know (but it is used in the "Lemniscate elliptic functions" article). However, "Fundamental period" for real functions is defined in the "Periodic function" article. There's also the "Fundamental pair of periods" article, but it doesn't mention the concept of minimal periods. So it needs to be defined somewhere (characterization by minimizing the absolute value of the period, etc.). A1E6 (talk) 21:44, 30 October 2021 (UTC)

Fair enough. Do you have a proposal for clearer or better defined nomenclature? I’m still planning to make a bunch of diagrams showing the behavior of these functions and others on the same lattices in the complex plane. –jacobolus (t) 22:58, 30 October 2021 (UTC)

The nomenclature is totally fine, it captures the meaning quite well. I understand what it means in the context of $\operatorname {sl}$ and $\operatorname {cl}$. But I thought you could write the general definition (for arbitrary complex functions) somewhere on Wikipedia when you brought it up. Can this concept be found somewhere in the literature? A1E6 (talk) 23:14, 30 October 2021 (UTC)

Maybe someone can make up a good definition at some point; for now I think we can just fall back on fundamental pair of periods. -jacobolus (t) 23:38, 30 October 2021 (UTC)

Tangent, and cosecant/secant/cotangent

Is there such thing as the "lemniscate tangent" function?

$\operatorname {tl} z={\frac {\operatorname {sl} z}{\operatorname {cl} z}}$

Or the analogues for the cosecant, secant, and cotangent?

$\operatorname {cscl} z={\frac {1}{\operatorname {sl} z}}$

$\operatorname {secl} z={\frac {1}{\operatorname {cl} z}}$

$\operatorname {cotl} z={\frac {\operatorname {cl} z}{\operatorname {sl} z}}$

DASL51984 ^{(Speak to me!)} 02:46, 14 May 2022 (UTC)

The Lemniscate function is already something like the "hyperbolic quartic tangent", the ratio of what might be called the hyperbolic quartic sine to the hyperbolic quartic cosine, based on the curve $x^{4}-y^{4}=1$ (compared to the hyperbolic sine, cosine, and tangent which are based on the curve $x^{2}-y^{2}=1$). This should be described in the article here. –jacobolus (t) 08:21, 18 May 2022 (UTC)

@DASL51984: If

$\operatorname {tl} z={\frac {\operatorname {sl} z}{\operatorname {cl} z}},$

then

$z=\int _{0}^{\operatorname {tl} z}{\frac {\mathrm {d} t}{\sqrt {t^{4}+6t^{2}+1}}}$

and

$\operatorname {sl} z={\frac {2\operatorname {tl} (z/2)}{\operatorname {tl} ^{2}(z/2)+1}}$

in a neigborhood of zero. The last formula is reminiscent of

$\sin z={\frac {2\tan(z/2)}{\tan ^{2}(z/2)+1}}.$

But I can't find the $\operatorname {tl}$ formulas anywhere on the internet. We'd have to find a reliable source discussing the "lemniscate tangent", otherwise we can't use it in the article. A1E6 (talk) 22:04, 16 June 2022 (UTC)

Neuman defines $\operatorname {arctl} x=\operatorname {arcsl} \left({\frac {x}{\sqrt[{4}]{1+x^{4}}}}\right).$ –jacobolus (t) 23:35, 11 July 2022 (UTC)

Interesting. He doesn't use the word "tangent", though. A1E6 (talk) 00:03, 12 July 2022 (UTC)

Move discussion in progress

There is a move discussion in progress on Talk:Gauss's constant which affects this page. Please participate on that page and not in this talk page section. Thank you. —RMCD bot 20:33, 25 June 2022 (UTC)

Cite updates

@Jacobolus: Are you saying these are correct? These are all things you updated.

• "Recherches sur les fonctions elliptiques" is the published title of the second part.
• It is not written in French.
• "Metodo per misurare la lemniscata" was published 1718–1723.
• "Giunte al primo schediasma sopra la Lemniscata" was published in 1710.
• It is not written in Italian.
• "Metodo per misurare la lemniscata, schediasma II" was published in 1710.
• It is not written in Italian.
• The book is titled: Opere Matematiche, vol. 2
• It is not written in Italian.
• Mathematical Works, Second Volume is not an accurate translation.

I make mistakes. I try to improve the articles. It is important that a reader can decipher the source cites from a print version.

I determined that the article order is the order in the 1911 reprint, logical or not.

I know translations may be flawed.

So may be the information in the archives: Internet Archive, etc.

Semantic Scholar appears to have the "Recherches sur les fonctions elliptiques" journal correct: Journal für die reine und angewandte Mathematik Apparently, it is commonly known as Crelles Journal. (De Gruyter does not list a journal in its cites.)

I am not fluent in German but I would say that the cite transcriptions in the archives are flawed. A good translation for "Dritter Band, in 4 heften" is "Third volume, in 4 issues". This would result in 2 (2): 101–181 and 3 (2): 160–190 for the 2 articles. (I know correcting an error this common is a hopeless cause and would not help a Wikipedia user.)

Correct the issues, don't revert to a flawed version.

Please fix the CS1 maintenance issues:

1. CS1 maint: url-status
2. CS1 maint: ref duplicates default

User-duck (talk) 11:12, 25 September 2022 (UTC)

No, what I am saying is that the version I had is legible to readers, and your updates made it less legible and more confusing (to be clear: I know this was not your intention). These are extended works which were published in a series of papers, but really it is the whole group of papers which should be considered one work for the purpose of this bibliography. So for instance Fagnano published (chronologically) "Method for measuring the lemniscate part 1", followed up with "Method for measuring the lemniscate part 2", then followed up a bit later with "Method for measuring the lemniscate, addendum to part 1" which logically fits between the first two papers. When the three were collected in his works later, they were re-ordered into the logical order. It doesn’t help readers to write the English translation "Method for measuring the lemniscate" three separate times, nor to write "in Italian" more than once, etc. To be honest the “cite” templates are not very flexible and don’t ideally work for this. I got the result to be legible, but apparently it bothers you that some kind of linter rules (which literally zero wiki readers will ever care about) are violated. If abusing the citation templates this way is an insurmountable problem, we can remove them and replace them with raw markup. –jacobolus (t) 14:56, 25 September 2022 (UTC)

Okay, I replaced the citation templates with manual markup wrapped in a 'cite' tag so that parenthetical references in other footnotes will link to the whole group of papers. Does that work? –jacobolus (t) 18:42, 25 September 2022 (UTC)

It is important that a reader can decipher the source cites Yes of course, the point is to make citations clear. This is why to the extent possible I also try to hyperlink directly to the relevant page(s). Tracking down these citations and writing them clearly took substantial effort, and I am happy to correct mistakes. –jacobolus (t) 15:07, 25 September 2022 (UTC)

I think the citations to Crelle's Journal are fine. This is one of the most famous and influential math journals of all time, and is traditionally cited as Crelle’s Journal or Crelle rather than its longer title (German for J. for Pure and Applied Math), perhaps partly because there are various other journals with similar names in English and French. Citing issues as 2 (2) or the like would be okay (this was in the very earliest years of the journal), but the official website of the journal now names the volumes by year rather than volume number – e.g. https://www.degruyter.com/journal/key/crll/1826/1/html – and I don’t think using the year is going to impede readers from finding the paper. The "(continuing from «citation of the first paper»)" parenthetical after Abel's second paper's title is not necessary to reprint in our citation here, because we directly cited the first paper immediately before. –jacobolus (t) 15:27, 25 September 2022 (UTC)

I updated the Crelle citations to include both the year and the volume number. Hopefully that clears up any confusion. –jacobolus (t) 18:43, 25 September 2022 (UTC)

Rewrite all power series + rewrite 'Hurwitz numbers'?

Should we rewrite the series

$\sum _{n=0}^{\infty }a_{n}z^{n}$

as

$\sum _{n=0}^{\infty }a_{n}'{\frac {z^{n}}{n!}}?$

This notation has the advantage that, in certain cases, the numbers $a_{n}'$ form an integer sequence (unlike the numbers $a_{n}$) and are often traceable to OEIS. Note, however, that some integer sequences appearing in this article seem to be novel in the sense that they are not yet on OEIS.

Also, I introduced new numbers ${\tilde {\mathrm {B} }}_{n}$ and ${\tilde {\mathrm {H} }}_{n}$. They simplify some equations, but they "obstruct" the original Bernoulli and Hurwitz numbers ($\mathrm {B} _{n}$ and $\mathrm {H} _{n}$) which are abundant in the literature. Should the 'Hurwitz numbers' section be rewritten? A1E6 (talk) 18:56, 18 December 2022 (UTC)

The power series seem a bit like trivia either way. Or maybe trivia is the wrong word; what I mean is, these are of interest to someone trying to do some specific technical thing with these functions, but are a bit of a tangent for most of the expected readers who will just skip over them. So I don’t have any strong preference. Which version do you think is clearer and more legible? Which version makes the explanation easiest? –jacobolus (t) 22:35, 18 December 2022 (UTC)

As an aside, should perhaps the section § Zeros, poles and symmetries be split apart? I feel like the second half of it feels out of scope given the heading. It could maybe be made into a new section (and can also be moved later if you like; not sure what the clearest section order is). –jacobolus (t) 22:38, 18 December 2022 (UTC)

Of course, the "Zeros, poles and symmetries" section can be split. A1E6 (talk) 01:23, 19 December 2022 (UTC)

And regarding the Hurwitz numbers: I don't know what's clearer. On the one hand, the Bernoulli numbers $\mathrm {B} _{n}$ have the neat definition

${\frac {z}{\mathrm {e} ^{z}-1}}=\sum _{n=0}^{\infty }\mathrm {B} _{n}{\frac {z^{n}}{n!}},$

but on the other hand,

$1+{\frac {z^{2}}{4}}-{\frac {z}{2}}{\frac {\operatorname {cn} (z/2;i)\operatorname {dn} (z/2;i)}{\operatorname {sl} (z/2)}}-{\frac {z}{2}}{\mathcal {E}}(z/2;i)=\sum _{n=1}^{\infty }\mathrm {H} _{n}{\frac {z^{n}}{n!}}$

is a "weird" function with pesky factors of $2$ all over the place. This was one of the reasons why I used ${\tilde {\mathrm {B} }}_{n}$ and ${\tilde {\mathrm {H} }}_{n}$ instead of $\mathrm {B} _{n}$ and $\mathrm {H} _{n}$. However, I realized that one could object that the numbers ${\tilde {\mathrm {H} }}_{n}$ and ${\tilde {\mathrm {B} }}_{n}$ don't appear in the literature. You know, what I'm doing is very similar to writing $\mathrm {e} ^{\tau \mathrm {i} }=1$ instead of $\mathrm {e} ^{2\pi \mathrm {i} }=1$ (if you're familiar with the proposals here [4] – it's a controversial topic; that sort of thing is probably not allowed on Wikipedia). But I guess it's OK if no one's actually complaining. A1E6 (talk) 01:37, 19 December 2022 (UTC)

Lemnatomic polynomials – algorithm

Given $\beta$, is there a fast algorithm for generating the polynomial $P_{\beta }(x)$ (or $\Lambda _{\beta }(x)$) appearing in the "Lemnatomic polynomials" section? A1E6 (talk) 18:31, 1 February 2023 (UTC)

I've just found an "acceptable" way of generating the $P_{\beta }(x)$ in Cox's Galois Theory book. I'll add an improved version of it (which utilizes Gauss' $M$ and $N$) to the article. A1E6 (talk) 16:12, 5 October 2024 (UTC)

Create a new article?

Do you think that it would be appropriate to rewrite $\operatorname {slh}$, $\operatorname {clh}$, $\operatorname {tlh}$ and $\operatorname {ctlh}$ to $\tan _{4}$, $\cot _{4}$, $\sin _{4}$ and $\cos _{4}$ respectively, and put these functions in a new article? I wonder what would be a good name for such an article. A1E6 (talk) 21:41, 2 June 2023 (UTC)

"Quartic trigonometric functions" or the like? You could try searching past literature to see if there's a name that will stand up to notability disputes. You might want to start with an article called "generalized trigonometric functions" or something. –jacobolus (t) 16:30, 6 June 2023 (UTC)

Are these alternate names in use? It's not our place to invent or promote new notations. —Tamfang (talk) 04:49, 7 July 2023 (UTC)

There would probably be notability issues. A1E6 (talk) 23:11, 8 July 2023 (UTC)

There are some papers using these names, but only a few and you are right that they are pretty obscure. (Though for that matter slh, clh, etc. are also pretty obscure.) –jacobolus (t) 01:57, 9 July 2023 (UTC)

Sorry for posting in an old discussion, but I think with recent additions to hyperbolic lemniscate functions it would be a good idea to create new article. Because this article is getting too big. To avoid notability issues new page could be called Hyberbolic lemniscate elliptic functions because it is already used in this article a lot. But instead of removing hyperbolic lemniscate elliptic funtions completely, we could leave the most important information there and a link to new article. Great Cosine (talk) 17:11, 26 July 2023 (UTC)

I'd frankly like to see this article slimmed and reorganized a bit, as it's a bit of an unfocused jumble. But I don't have the mental bandwidth to do it anytime in the near future. –jacobolus (t) 17:13, 26 July 2023 (UTC)

Sources?

Hi @Reformbenediktiner, and thanks for your contributions. Do you have sources for the bunch of material you just added? Remember, information added to Wikipedia must be "Verifiable" in "Reliable Sources" and cannot be "Original Research". –jacobolus (t) 07:50, 25 July 2023 (UTC)

Good forenoon, dear user Jacobolus!

You are welcome. Yes, I have sources. And yes, I will add them as soon as I can. But my works are not finished yet. Please, do not be afraid! Of course these are many new mathematical formula informations. But I will enter references in fact. Give me time! I will make everything very accurately and also very clearly. Maybe I should say one special thing right at the beginning because some Wikipedia users saw me working and they had their opinion about my many formula editings. I do not mess around. I put everything on the gold scales and check all formulas very accurately for total correctness. I carve and gouge, trim and sand, wood and carpenter, polish and smooth until everything is brilliant as a diamond. This is my personal way of working. Of course, this way of working is also related to my intense enthusiasm and gigantic love for infinitesimal mathematics. In my spare time I research all the formulas very meticulously and in great detail. My love of mathematics and my meticulous and detailed way of working as well as my enormous diligence are of course also very closely related to my special autistic way. Yes, I really do have the Asperger's Syndrome and it has been thoroughly diagnosed several times in my life. Only one person of hundred to thousand persons in Europe does have the Asperger autism. And I do belong to these one percent til one thoundsandth. But I am really proud of it. And I am glad about my many discoveries in the world of mathematics, in the big empire of analytical functions that I discover. I really love mathematics and especially the analysis, the infinitesimal calculation. Therefore I enter as many formulas as I can. But I also keep the well structured fabric and texture of the article as positive as possible. For every reader should be extremely happy and about this article with all his heart and be zestful and enthusiastic about the facts, that the knowledge of the lemniscatic elliptic functions is explained so thoroughly and so super brilliant.That's why I try so extremely intensive effort, I really try to give everything. Because I want to produce an extremely good article like a beautiful giant shining star. I keep creating, I consequently work on. And yes, of course I will add references indeed. Just give me time! Yours faithfully and sincerely!! Lion Emil Jann Fiedler also known as Reformbenediktiner Reformbenediktiner (talk) 08:54, 25 July 2023 (UTC)

And I am glad about my many discoveries in the world of mathematics, in the big empire of analytical functions that I discover. – Discovering formulas is wonderful, and well worth spending time on, but do note that Wikipedia is not a venue for publishing new research. Everything you add here needs to have been written down before in the existing published literature. All the best. –jacobolus (t) 10:09, 25 July 2023 (UTC)

Some of the content you added is original research, and some violates WP:INDISCRIMINATE. I had to remove it. Regarding the quintic equations: We already have a theta function solution here: http://en.wiki.x.io/wiki/Bring_radical#Other_characterizations

Unlike your solution, it's properly sourced, it's simpler and it gives all complex roots. Note that

$\varphi (\tau )={\frac {\theta _{4}(-1/\tau )}{\theta _{4}(-2/\tau )}},\quad \psi (\tau )={\frac {\theta _{4}(\tau )}{\theta _{4}(2\tau )}}$

for all $\tau \in \mathbb {C}$ such that $\Im (\tau )>0$. A1E6 (talk) 16:49, 25 July 2023 (UTC)

@Reformbenediktiner I didn't try to track down Hermite's paper. Does it actually make claims about the hyperbolic lemniscate functions? Or do you have another source for that? –jacobolus (t) 05:41, 14 August 2023 (UTC)

Good morning, dear user Jacobolus! I really appreciate you and thank you for not deleting anything but maintaining everything. I say this because there are some other users who have all too often labeled and judged my entered formulas as theory finding and original research and then these users deleted all my entries again and again. I am very glad you are not one of those destructive types of users. Before I mention the hyperbolic lemniscate functions in the aspect of the Hermite research result and the quintic equation, I just took the Hermite source on page 258 and copied the formula out of his essay. Then I just made regular calculation algorithms that are very well known and everyone of us could create. In the last step I just saw immediately in the results that the modulus and the Pythagorean complementary modulus can be presented in a very easy way by using the hyperbolic lemniscate functions. And it was listed at a special point in the same article in a section above. So I decided to enter these results exactly in that article. Reformbenediktiner (talk) 05:58, 14 August 2023 (UTC)

just made regular calculation algorithms that are very well known – If the relationship to lemniscate functions hasn't been pointed out in published literature, that sounds like original research to me. This section might still be better to remove, and the general subject left to the article Bring radical. –jacobolus (t) 06:34, 14 August 2023 (UTC)

I have one more sincere request for you. Please allow me to immediately write the abbreviation $\mathrm {aslh}$ instead of $\mathrm {slh} ^{-1}$ and put the rectangular brackets back on! I decide to do that because am afraid that instead of the inverse function, someone means or understands seriously the reciprocal function instead of that. And that would give me goosebumps in a special way. It is this expression of minus one in the exponent position. It has been and is all too often misleading. I hope you won't get mad or angry if I seriously allow myself this move at this point. I'm a perfectionist! I just can't act any other way. It's a compulsion in me, it's a quirk that I can't give in to! I'm telling the truth here. Reformbenediktiner (talk) 06:13, 14 August 2023 (UTC)

Do you have a published source which uses the name 'aslh'? –jacobolus (t) 06:36, 14 August 2023 (UTC)

I'm concerned that a whole bunch of material has been added to this article that (perhaps) can't actually be found in any published sources. Wikipedia is not the place to make up new names, publish novel identities, write new proofs, etc. I haven't wanted to wade through because it looks like a lot of work. But Reformbenediktiner if you could please add sources directly covering everything you have added that would be helpful. Otherwise any unsourced parts are likely to be removed. It's nothing personal and nobody wants to give you a hard time. It would just be better to publish new results somewhere else, e.g. in your own research paper. –jacobolus (t) 06:41, 14 August 2023 (UTC)

Eisenstein's number-theoretic paper

In the section "A quartic analog of the Legendre symbol", we have

If $a$ and $p$ are coprime, then there exist numbers $p'\in \mathbb {Z} [i]$ such that

$\left({\frac {a}{p}}\right)_{4}=\prod _{p'}{\frac {\operatorname {sl} (2\varpi ap'/p)}{\operatorname {sl} (2\varpi p'/p)}}.$

However, note that it says "there exist numbers" and it doesn't say what the numbers are – that's the problem with Ogawa's paper – Ogawa attempts to say what the numbers are but he (perhaps on purpose) doesn't define a certain quantity he's using and instead relies on references.

This problem is in fact resolved in the following [5] paper of Eisenstein (page 192, equation 10') – it is known what the numbers are, just as in the trigonometric analog. I'll copy the relevant equation here:

$\left[{\frac {n}{m}}\right]=\prod {\frac {\varphi (nt)}{\varphi (t)}}$

where Eisenstein writes $\varphi =\operatorname {sl}$, $t=r\omega /m$ and $\omega =2\varpi$.

The product in that equation runs over numbers that are defined in the paper above that equation. Unfortunately, I don't have time to study Eisenstein's paper right now. If you have time to translate it to English, understand it and publish the (full) theorem on Wikipedia, I would be so grateful! A1E6 (talk) 14:56, 22 April 2024 (UTC)

References

Unit lemniscate – alternative

Do you think I should add an alternative, perhaps "more natural" characterization of the unit lemniscate to this article? A1E6 (talk) 08:11, 9 May 2024 (UTC)

Writing it this way seems unnecessarily confusing, to be honest. Mentioning various properties/characterizations is fine of course, but I'd start with just one. Also, do you have sources? –jacobolus (t) 18:05, 9 May 2024 (UTC)

Oh yes, I have a source for the angular characterization. I'll add it to the article. But what is the best place to have various characterizations of the unit lemniscate on Wikipedia? The lemniscatic functions are the thing that make the unit lemniscate relevant, so I thought this article was the best place (note that we don't have a "unit lemniscate" article).

I thought my addition was appropriate in the light of the fact that this article "hosts" other stuff which is closely related to the lemniscatic functions but which doesn't have its own article, for example: inverse lemniscatic functions, unit-diameter circle, Hurwitz numbers, Gauss' functions ($M,N,S,T$), hyperbolic lemniscatic functions and lemnatomic polynomials.

I believe each of the characterizations is relevant for the article. The angular characterization explains where "the unity" in the unit lemniscate is; just like we know where "the unity" in the unit circle or the unit-diameter circle is. Foci are used in one of your pictures and the explicit coordinate characterization is used in the arc length proof. A1E6 (talk) 18:15, 9 May 2024 (UTC)

I'm not saying it's "inappropriate". I just wonder if readers will find it overwhelming. I think this article has overall grown quite a bit beyond what the narrative prose necessarily supports. It has a long list of detailed formulas and technical information (plenty of it added by me; I'm not trying to point fingers), but not as much connective prose explaining why that matters, etc. –jacobolus (t) 19:20, 9 May 2024 (UTC)

If you think the article is bloated: I can remove lots of stuff in just one edit, but I'm afraid that some of these changes would be considered controversial (everything would be explained on the Talk page, of course). A1E6 (talk) 19:32, 9 May 2024 (UTC)

I'm not saying it's bloated. I'm saying there's (in my opinion) not enough explanatory text alongside the technical information to bring readers along for a clear narrative ride. It serves as (hopefully useful) reference material, but it would be nice to figure out how to clearly explain what's going on in such a way that someone who is a nonspecialist could read big chunks, maybe skimming past a few bits they weren't interested in, and come away with a clear story about what the lemniscate functions are about and why they are interesting. –jacobolus (t) 20:04, 9 May 2024 (UTC)

That would need someone very good at writing English prose (I'm not the guy :D). Maybe we could turn it into a featured article one day... A1E6 (talk) 20:07, 9 May 2024 (UTC)

What is tilde?

Throughout the article ${\tilde {sl}}$ appears, but I cannot seem to find where this is defined. Tito Omburo (talk) 15:26, 24 July 2024 (UTC)

It's defined in the "Relation to geometric shapes" section. Namely:

Alternatively, just as the unit circle $x^{2}+y^{2}=1$ is parametrized in terms of the arc length $s$ from the point $(1,0)$ by

$(x(s),y(s))=(\cos s,\sin s),$

${\mathcal {L}}$ is parametrized in terms of the arc length $s$ from the point $(1,0)$ by

$(x(s),y(s))=\left({\frac {\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}},{\frac {\operatorname {sl} s\operatorname {cl} s}{\sqrt {1+\operatorname {sl} ^{2}s}}}\right)=\left(\color {green}{\tilde {\operatorname {cl} }}\,s,\color {green}{\tilde {\operatorname {sl} }}\,s\right).$

It's defined by that for all $s\in \mathbb {R}$ (the arc length can be taken in a positive or negative sense) and by analytic continuation elsewhere in the complex plane – the tilde functions are in fact meromorphic and it turns out that

${\tilde {\operatorname {sl} }}\,z=\operatorname {cd} (z;i)\operatorname {sd} (z;i),$

${\tilde {\operatorname {cl} }}\,z=\operatorname {cd} (z;i)\operatorname {nd} (z;i)$

for all $z\in \mathbb {C}$, with $\operatorname {cd} ,\operatorname {sd} ,\operatorname {nd}$ being the Jacobi elliptic functions.

The tilde functions don't appear in references but they are describing a certain concept that can be found in at least two references. In the references, they instead use notation for Jacobi elliptic functions. Since this article is about lemniscatic functions and not general Jacobi elliptic functions, I thought that, for the purposes of this article, giving the functions some "lemniscatic name" is appropriate. But perhaps the reader should be warned that this name doesn't appear in references. A1E6 (talk) 12:54, 26 July 2024 (UTC)

References

Hyperbolic Lemniscate Functions and a YouTube Video

I am wondering how the section of this article on hyperbolic lemniscate functions and the quartic Fermat curve (aka squircle) relates to the following YouTube video: https://www.youtube.com/watch?v=mAzIE5OkqWE&t=3s It amounts to the following equation:

$(*){\mbox{cl}}({\sqrt {2}}t)={\frac {\cos _{4}^{2}(t)-\sin _{4}^{2}(t)}{\cos _{4}^{2}(t)+\sin _{4}^{2}(t)}}$

To see this, compare the video to the picture of the squircle http://en.wiki.x.io/wiki/Lemniscate_elliptic_functions#/media/File:Quartic_Fermat_curve.png in this article. The relation shown in the video has $l={\sqrt {2}}t$. Here $l$ is the arc length of the lemniscate from the point $C$ in the video to $(1,0)$. Hence ${\mbox{cl}}({\sqrt {2}}t)={\mbox{cl}}(l)=AC$. The point $B$ in the video is the radial projection of the point $(\cos _{4}(t),\sin _{4}(t))$ on the squircle to the lemniscate. Hence

$B=\left({\frac {\cos _{4}(t){\sqrt {\cos _{4}^{2}(t)-\sin _{4}^{2}(t)}}}{cos_{4}^{2}(t)+\sin _{4}^{2}(t)}},{\frac {\sin _{4}(t){\sqrt {\cos _{4}^{2}(t)-\sin _{4}^{2}(t)}}}{cos_{4}^{2}(t)+\sin _{4}^{2}(t)}}\right)$

The relation shown in the video has $AC=AB^{2}$. Substituting for $AC$ and $AB$ and simplifying, we obtain $(*)$. Any comments? Fiedorow (talk) 22:32, 8 November 2024 (UTC)

Neat! However, anonymous YouTube videos don't count as a "reliable source" by Wikipedia standards. –jacobolus (t) 01:07, 9 November 2024 (UTC)

The relation depicted in the video has a nice proof. See my comment to the video. I am asking whether there is a relation to the equations @Reformbenediktiner posted in this Wikipedia article. Fiedorow (talk) 01:49, 9 November 2024 (UTC)

Here is a direct link to the proof of the relation shown in the video:

https://drive.google.com/file/d/1idxRw7LQ4LEP4qDDHG40Ou0pr2tdNNYU/view?usp=drivesdk Fiedorow (talk) 01:54, 9 November 2024 (UTC)

Yes, but whether a relation is provable or not doesn't really bear on whether it should be in Wikipedia. Wikipedia is a place for summarizing the content of reliable sources, not republishing original provable statements found on the open internet. –jacobolus (t) 03:06, 9 November 2024 (UTC)

I am not proposing that this relation should be included in the body of the article. The reason I became interested in this

question is that I am looking for interesting material to incorporate into an undergraduate analysis book I am writing:

https://drive.google.com/file/d/1hMZuRxP3VvKBcSaVBTLABeVWjmb-9AEP/view?usp=drivesdk

I already included a section on lemniscate elliptic functions, for which this Wikipedia article was very helpful. Then I

stumbled across this video which seems like very suitable material in the same vein. Hence I am looking for some

things I could write connecting these topics and also references I could provide to readers for further reading.

However I do notice that the External Links section of this article already contains a link to Matt Parker's YouTube video on the area of a

squircle. It seems to me that this YouTube video would be a suitable addition to that section with a note mentioning equation (*).

However I am not sure how such an addition should appear in this article. Should the link and the equation both go into the External

Links section or should the equation be added to the Notes section? Fiedorow (talk) 14:53, 9 November 2024 (UTC)

If you have the source files, I think a still image extracted from this example might be good in the article. I like this example, very intuitive. Tito Omburo (talk) 17:42, 9 November 2024 (UTC)

Here is a link to a screen capture of the video:

https://drive.google.com/file/d/11sXch55HwbnviaK3tWPT5ognPUjSnAlu/view?usp=drivesdk

and here is a downloadable link to the video:

https://www.reddit.com/r/educationalgifs/comments/1197rmc/bernoulli_lemniscate_and_the_squircle_a/#lightbox Fiedorow (talk) 18:15, 9 November 2024 (UTC)

I propose adding an External Link to the article as follows:

• Veerappan Ramalingam, Muthu (2023). "Bernoulli Lemniscate and the Squircle $||$ A remarkable Geometric fun fact!!?". Act of Learning. YouTube. Archived from the original on 2024-11-10. Relation shown in the video amounts to ${\mbox{cl}}({\sqrt {2}}t)={\frac {\cos _{4}^{2}(t)-\sin _{4}^{2}(t)}{\cos _{4}^{2}(t)+\sin _{4}^{2}(t)}}$

Any objections? Fiedorow (talk) 14:29, 11 November 2024 (UTC)

I have found the name of the author of that video. His name is Muthu Veerappan Ramalingam. He is a business analyst for Amazon India. I will add his name to the link above. I am trying to contact him on Facebook to ask him for his sources for that video. Fiedorow (talk) 15:39, 11 November 2024 (UTC)