Nodal decomposition

In category theory, an abstract mathematical discipline, a nodal decomposition^[1] of a morphism $\varphi :X\to Y$ is a representation of $\varphi$ as a product $\varphi =\sigma \circ \beta \circ \pi$ , where $\pi$ is a strong epimorphism,^[2]^[3]^[4] $\beta$ a bimorphism, and $\sigma$ a strong monomorphism.^[5]^[3]^[4]

Uniqueness and notations

If it exists, the nodal decomposition is unique up to an isomorphism in the following sense: for any two nodal decompositions $\varphi =\sigma \circ \beta \circ \pi$ and $\varphi =\sigma '\circ \beta '\circ \pi '$ there exist isomorphisms $\eta$ and $\theta$ such that

\pi '=\eta \circ \pi ,

\beta =\theta \circ \beta '\circ \eta ,

\sigma '=\sigma \circ \theta .

This property justifies some special notations for the elements of the nodal decomposition:

{\begin{aligned}&\pi =\operatorname {coim} _{\infty }\varphi ,&&P=\operatorname {Coim} _{\infty }\varphi ,\\&\beta =\operatorname {red} _{\infty }\varphi ,&&\\&\sigma =\operatorname {im} _{\infty }\varphi ,&&Q=\operatorname {Im} _{\infty }\varphi ,\end{aligned}}

– here $\operatorname {coim} _{\infty }\varphi$ and $\operatorname {Coim} _{\infty }\varphi$ are called the nodal coimage of $\varphi$ , $\operatorname {im} _{\infty }\varphi$ and $\operatorname {Im} _{\infty }\varphi$ the nodal image of $\varphi$ , and $\operatorname {red} _{\infty }\varphi$ the nodal reduced part of $\varphi$ .

In these notations the nodal decomposition takes the form

\varphi =\operatorname {im} _{\infty }\varphi \circ \operatorname {red} _{\infty }\varphi \circ \operatorname {coim} _{\infty }\varphi .

Connection with the basic decomposition in pre-abelian categories

In a pre-abelian category ${\mathcal {K}}$ each morphism $\varphi$ has a standard decomposition

\varphi =\operatorname {im} \varphi \circ \operatorname {red} \varphi \circ \operatorname {coim} \varphi

,

called the basic decomposition (here $\operatorname {im} \varphi =\ker(\operatorname {coker} \varphi )$ , $\operatorname {coim} \varphi =\operatorname {coker} (\ker \varphi )$ , and $\operatorname {red} \varphi$ are respectively the image, the coimage and the reduced part of the morphism $\varphi$ ).

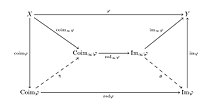
If a morphism $\varphi$ in a pre-abelian category ${\mathcal {K}}$ has a nodal decomposition, then there exist morphisms $\eta$ and $\theta$ which (being not necessarily isomorphisms) connect the nodal decomposition with the basic decomposition by the following identities:

\operatorname {coim} _{\infty }\varphi =\eta \circ \operatorname {coim} \varphi ,

\operatorname {red} \varphi =\theta \circ \operatorname {red} _{\infty }\varphi \circ \eta ,

\operatorname {im} _{\infty }\varphi =\operatorname {im} \varphi \circ \theta .

Categories with nodal decomposition

A category ${\mathcal {K}}$ is called a category with nodal decomposition^[1] if each morphism $\varphi$ has a nodal decomposition in ${\mathcal {K}}$ . This property plays an important role in constructing envelopes and refinements in ${\mathcal {K}}$ .

In an abelian category ${\mathcal {K}}$ the basic decomposition

\varphi =\operatorname {im} \varphi \circ \operatorname {red} \varphi \circ \operatorname {coim} \varphi

is always nodal. As a corollary, all abelian categories have nodal decomposition.

If a pre-abelian category ${\mathcal {K}}$ is linearly complete,^[6] well-powered in strong monomorphisms^[7] and co-well-powered in strong epimorphisms,^[8] then ${\mathcal {K}}$ has nodal decomposition.^[9]

More generally, suppose a category ${\mathcal {K}}$ is linearly complete,^[6] well-powered in strong monomorphisms,^[7] co-well-powered in strong epimorphisms,^[8] and in addition strong epimorphisms discern monomorphisms^[10] in ${\mathcal {K}}$ , and, dually, strong monomorphisms discern epimorphisms^[11] in ${\mathcal {K}}$ , then ${\mathcal {K}}$ has nodal decomposition.^[12]

The category Ste of stereotype spaces (being non-abelian) has nodal decomposition,^[13] as well as the (non-additive) category SteAlg of stereotype algebras .^[14]

Notes

^ ^a ^b Akbarov 2016, p. 28.
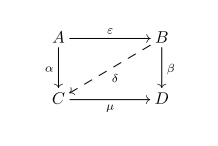
^ An epimorphism $\varepsilon :A\to B$ is said to be strong, if for any monomorphism $\mu :C\to D$ and for any morphisms $\alpha :A\to C$ and $\beta :B\to D$ such that $\beta \circ \varepsilon =\mu \circ \alpha$ there exists a morphism $\delta :B\to C$ , such that $\delta \circ \varepsilon =\alpha$ and $\mu \circ \delta =\beta$ .
^ ^a ^b Borceux 1994.
^ ^a ^b Tsalenko & Shulgeifer 1974.
^ A monomorphism $\mu :C\to D$ is said to be strong, if for any epimorphism $\varepsilon :A\to B$ and for any morphisms $\alpha :A\to C$ and $\beta :B\to D$ such that $\beta \circ \varepsilon =\mu \circ \alpha$ there exists a morphism $\delta :B\to C$ , such that $\delta \circ \varepsilon =\alpha$ and $\mu \circ \delta =\beta$
^ ^a ^b A category ${\mathcal {K}}$ is said to be linearly complete, if any functor from a linearly ordered set into ${\mathcal {K}}$ has direct and inverse limits.
^ ^a ^b A category ${\mathcal {K}}$ is said to be well-powered in strong monomorphisms, if for each object $X$ the category $\operatorname {SMono} (X)$ of all strong monomorphisms into $X$ is skeletally small (i.e. has a skeleton which is a set).
^ ^a ^b A category ${\mathcal {K}}$ is said to be co-well-powered in strong epimorphisms, if for each object $X$ the category $\operatorname {SEpi} (X)$ of all strong epimorphisms from $X$ is skeletally small (i.e. has a skeleton which is a set).
^ Akbarov 2016, p. 37.
^ It is said that strong epimorphisms discern monomorphisms in a category ${\mathcal {K}}$ , if each morphism $\mu$ , which is not a monomorphism, can be represented as a composition $\mu =\mu '\circ \varepsilon$ , where $\varepsilon$ is a strong epimorphism which is not an isomorphism.
^ It is said that strong monomorphisms discern epimorphisms in a category ${\mathcal {K}}$ , if each morphism $\varepsilon$ , which is not an epimorphism, can be represented as a composition $\varepsilon =\mu \circ \varepsilon '$ , where $\mu$ is a strong monomorphism which is not an isomorphism.
^ Akbarov 2016, p. 31.
^ Akbarov 2016, p. 142.
^ Akbarov 2016, p. 164.