Meissel–Mertens constant
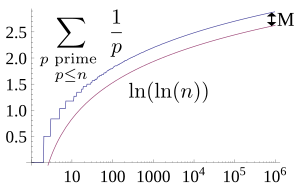
The Meissel–Mertens constant (named after Ernst Meissel and Franz Mertens), also referred to as the Mertens constant, Kronecker's constant (after Leopold Kronecker), Hadamard–de la Vallée-Poussin constant (after Jacques Hadamard and Charles Jean de la Vallée-Poussin), or the prime reciprocal constant, is a mathematical constant in number theory, defined as the limiting difference between the harmonic series summed only over the primes and the natural logarithm of the natural logarithm:
Here γ is the Euler–Mascheroni constant, which has an analogous definition involving a sum over all integers (not just the primes).

The value of M is approximately
Mertens' second theorem establishes that the limit exists.
The fact that there are two logarithms (log of a log) in the limit for the Meissel–Mertens constant may be thought of as a consequence of the combination of the prime number theorem and the limit of the Euler–Mascheroni constant.
In popular culture
[edit]The Meissel-Mertens constant was used by Google when bidding in the Nortel patent auction. Google posted three bids based on mathematical numbers: $1,902,160,540 (Brun's constant), $2,614,972,128 (Meissel–Mertens constant), and $3.14159 billion (π).[1]
See also
[edit]References
[edit]- ^ "Google's strange bids for Nortel patents". FinancialPost.com. Reuters. July 5, 2011. Retrieved 2011-08-16.
External links
[edit]- Weisstein, Eric W. "Mertens Constant". MathWorld.
- On the remainder in a series of Mertens (postscript file)

![{\displaystyle M=\lim _{n\rightarrow \infty }\left(\sum _{\scriptstyle p{\text{ prime}} \atop \scriptstyle p\leq n}{\frac {1}{p}}-\ln(\ln n)\right)=\gamma +\sum _{p}\left[\ln \!\left(1-{\frac {1}{p}}\right)+{\frac {1}{p}}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/458f1b3f6afe8490c8f84dd45f1f895a8447f9e8)

