Image
Name
First described
Equation
Comment
Circle
r
=
k
{\displaystyle r=k}
The trivial spiral
Archimedean spiral (also arithmetic spiral )
c. 320 BC
r
=
a
+
b
⋅
θ
{\displaystyle r=a+b\cdot \theta }
Fermat's spiral (also parabolic spiral)
1636[ 1]
r
2
=
a
2
⋅
θ
{\displaystyle r^{2}=a^{2}\cdot \theta }
Euler spiral (also Cornu spiral or polynomial spiral)
1696[ 2]
x
(
t
)
=
C
(
t
)
,
{\displaystyle x(t)=\operatorname {C} (t),\,}
y
(
t
)
=
S
(
t
)
{\displaystyle y(t)=\operatorname {S} (t)}
Using Fresnel integrals [ 3]
Hyperbolic spiral (also reciprocal spiral )
1704
r
=
a
θ
{\displaystyle r={\frac {a}{\theta }}}
Lituus
1722
r
2
⋅
θ
=
k
{\displaystyle r^{2}\cdot \theta =k}
Logarithmic spiral (also known as equiangular spiral )
1638[ 4]
r
=
a
⋅
e
b
⋅
θ
{\displaystyle r=a\cdot e^{b\cdot \theta }}
Approximations of this are found in nature
Fibonacci spiral
Circular arcs connecting the opposite corners of squares in the Fibonacci tiling
Approximation of the golden spiral
Golden spiral
r
=
φ
2
⋅
θ
π
{\displaystyle r=\varphi ^{\frac {2\cdot \theta }{\pi }}\,}
Special case of the logarithmic spiral
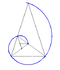
Spiral of Theodorus (also known as Pythagorean spiral )
c. 500 BC Contiguous right triangles composed of one leg with unit length and the other leg being the hypotenuse of the prior triangle
Approximates the Archimedean spiral
Involute
1673
x
(
t
)
=
r
(
cos
(
t
+
a
)
+
t
sin
(
t
+
a
)
)
,
{\displaystyle x(t)=r(\cos(t+a)+t\sin(t+a)),}
y
(
t
)
=
r
(
sin
(
t
+
a
)
−
t
cos
(
t
+
a
)
)
{\displaystyle y(t)=r(\sin(t+a)-t\cos(t+a))}
Involutes of a circle appear like Archimedean spirals
Helix
r
(
t
)
=
1
,
{\displaystyle r(t)=1,\,}
θ
(
t
)
=
t
,
{\displaystyle \theta (t)=t,\,}
z
(
t
)
=
t
{\displaystyle z(t)=t}
A three-dimensional spiral
Rhumb line (also loxodrome)
Type of spiral drawn on a sphere
Cotes's spiral
1722
1
r
=
{
A
cosh
(
k
θ
+
ε
)
A
exp
(
k
θ
+
ε
)
A
sinh
(
k
θ
+
ε
)
A
(
k
θ
+
ε
)
A
cos
(
k
θ
+
ε
)
{\displaystyle {\frac {1}{r}}={\begin{cases}A\cosh(k\theta +\varepsilon )\\A\exp(k\theta +\varepsilon )\\A\sinh(k\theta +\varepsilon )\\A(k\theta +\varepsilon )\\A\cos(k\theta +\varepsilon )\\\end{cases}}}
Solution to the two-body problem for an inverse-cube central force
Poinsot's spirals
r
=
a
⋅
csch
(
n
⋅
θ
)
,
{\displaystyle r=a\cdot \operatorname {csch} (n\cdot \theta ),\,}
r
=
a
⋅
sech
(
n
⋅
θ
)
{\displaystyle r=a\cdot \operatorname {sech} (n\cdot \theta )}
Nielsen's spiral
1993[ 5]
x
(
t
)
=
ci
(
t
)
,
{\displaystyle x(t)=\operatorname {ci} (t),\,}
y
(
t
)
=
si
(
t
)
{\displaystyle y(t)=\operatorname {si} (t)}
A variation of Euler spiral, using sine integral and cosine integrals
Polygonal spiral
Special case approximation of arithmetic or logarithmic spiral
Fraser's Spiral
1908
Optical illusion based on spirals
Conchospiral
r
=
μ
t
⋅
a
,
{\displaystyle r=\mu ^{t}\cdot a,\,}
θ
=
t
,
{\displaystyle \theta =t,\,}
z
=
μ
t
⋅
c
{\displaystyle z=\mu ^{t}\cdot c}
A three-dimensional spiral on the surface of a cone.
Calkin–Wilf spiral
Ulam spiral (also prime spiral)
1963
Sacks spiral
1994
Variant of Ulam spiral and Archimedean spiral.
Seiffert's spiral
2000[ 6]
r
=
sn
(
s
,
k
)
,
{\displaystyle r=\operatorname {sn} (s,k),\,}
θ
=
k
⋅
s
{\displaystyle \theta =k\cdot s}
z
=
cn
(
s
,
k
)
{\displaystyle z=\operatorname {cn} (s,k)}
Spiral curve on the surface of a sphere using the Jacobi elliptic functions [ 7]
Tractrix spiral
1704[ 8]
{
r
=
A
cos
(
t
)
θ
=
tan
(
t
)
−
t
{\displaystyle {\begin{cases}r=A\cos(t)\\\theta =\tan(t)-t\end{cases}}}
Pappus spiral
1779
{
r
=
a
θ
ψ
=
k
{\displaystyle {\begin{cases}r=a\theta \\\psi =k\end{cases}}}
3D conical spiral studied by Pappus and Pascal [ 9]
Doppler spiral
x
=
a
⋅
(
t
⋅
cos
(
t
)
+
k
⋅
t
)
,
{\displaystyle x=a\cdot (t\cdot \cos(t)+k\cdot t),\,}
y
=
a
⋅
t
⋅
sin
(
t
)
{\displaystyle y=a\cdot t\cdot \sin(t)}
2D projection of Pappus spiral[ 10]
Atzema spiral
x
=
sin
(
t
)
t
−
2
⋅
cos
(
t
)
−
t
⋅
sin
(
t
)
,
{\displaystyle x={\frac {\sin(t)}{t}}-2\cdot \cos(t)-t\cdot \sin(t),\,}
y
=
−
cos
(
t
)
t
−
2
⋅
sin
(
t
)
+
t
⋅
cos
(
t
)
{\displaystyle y=-{\frac {\cos(t)}{t}}-2\cdot \sin(t)+t\cdot \cos(t)}
The curve that has a catacaustic forming a circle. Approximates the Archimedean spiral.[ 11]
Atomic spiral
2002
r
=
θ
θ
−
a
{\displaystyle r={\frac {\theta }{\theta -a}}}
This spiral has two asymptotes ; one is the circle of radius 1 and the other is the line
θ
=
a
{\displaystyle \theta =a}
[ 12]
Galactic spiral
2019
{
d
x
=
R
⋅
y
x
2
+
y
2
d
θ
d
y
=
R
⋅
[
ρ
(
θ
)
−
x
x
2
+
y
2
]
d
θ
{
x
=
∑
d
x
y
=
∑
d
y
+
R
{\displaystyle {\begin{cases}dx=R\cdot {\frac {y}{\sqrt {x^{2}+y^{2}}}}d\theta \\dy=R\cdot \left[\rho (\theta )-{\frac {x}{\sqrt {x^{2}+y^{2}}}}\right]d\theta \end{cases}}{\begin{cases}x=\sum dx\\\\\\y=\sum dy+R\end{cases}}}
The differential spiral equations were developed to simulate the spiral arms of disc galaxies, have 4 solutions with three different cases:
ρ
<
1
,
ρ
=
1
,
ρ
>
1
{\displaystyle \rho <1,\rho =1,\rho >1}
ρ
{\displaystyle \rho }
ρ
<
1
{\displaystyle \rho <1}
ρ
=
1
,
{\displaystyle \rho =1,}
ρ
>
1
,
{\displaystyle \rho >1,}
−
θ
{\displaystyle -\theta }
[ 13] [predatory publisher
![{\displaystyle {\begin{cases}dx=R\cdot {\frac {y}{\sqrt {x^{2}+y^{2}}}}d\theta \\dy=R\cdot \left[\rho (\theta )-{\frac {x}{\sqrt {x^{2}+y^{2}}}}\right]d\theta \end{cases}}{\begin{cases}x=\sum dx\\\\\\y=\sum dy+R\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/47cba127b869ed1f803e339d0dd8f979c175be01)
