D5 polytope
 5-demicube |
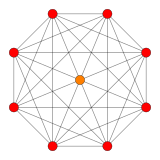 5-orthoplex |
In 5-dimensional geometry, there are 23 uniform polytopes with D5 symmetry, 8 are unique, and 15 are shared with the B5 symmetry. There are two special forms, the 5-orthoplex, and 5-demicube with 10 and 16 vertices respectively.
They can be visualized as symmetric orthographic projections in Coxeter planes of the D6 Coxeter group, and other subgroups.
Graphs
[edit]Symmetric orthographic projections of these 8 polytopes can be made in the D5, D4, D3, A3, Coxeter planes. Ak has [k+1] symmetry, Dk has [2(k-1)] symmetry. The B5 plane is included, with only half the [10] symmetry displayed.
These 8 polytopes are each shown in these 5 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| # | Coxeter plane projections | Coxeter diagram Schläfli symbol Johnson and Bowers names | ||||
|---|---|---|---|---|---|---|
| [10/2] | [8] | [6] | [4] | [4] | ||
| B5 | D5 | D4 | D3 | A3 | ||
| 1 | 
|

|
|
|

|
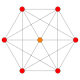
h{4,3,3,3} 5-demicube Hemipenteract (hin) |
| 2 | 
|
|
|

|
|
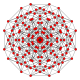
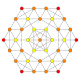
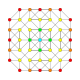
h2{4,3,3,3} Cantic 5-cube Truncated hemipenteract (thin) |
| 3 | 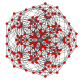
|
|
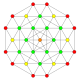
|

|

|
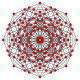
h3{4,3,3,3} Runcic 5-cube Small rhombated hemipenteract (sirhin) |
| 4 | 
|
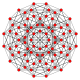
|
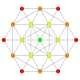
|

|

|
h4{4,3,3,3} Steric 5-cube Small prismated hemipenteract (siphin) |
| 5 | 
|

|
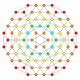
|

|
|
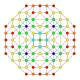
h2,3{4,3,3,3} Runcicantic 5-cube Great rhombated hemipenteract (girhin) |
| 6 | 
|

|
|

|
|
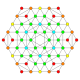
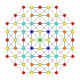
h2,4{4,3,3,3} Stericantic 5-cube Prismatotruncated hemipenteract (pithin) |
| 7 | 
|

|
|
|
|
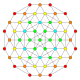
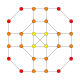
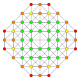
h3,4{4,3,3,3} Steriruncic 5-cube Prismatorhombated hemipenteract (pirhin) |
| 8 | 
|

|
|

|

|
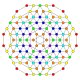
h2,3,4{4,3,3,3} Steriruncicantic 5-cube Great prismated hemipenteract (giphin) |
References
[edit]- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "5D uniform polytopes (polytera)".
