User:Zen-in/sandbox

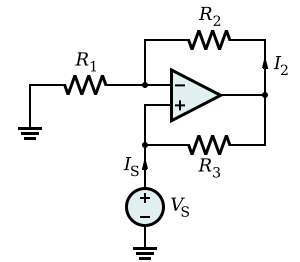
Negative impedance converter

Transfer function derivation

First, assigning V_a = voltage at + terminal = V_s and assigning V_b = voltage at - terminal and assigning V_o = voltage at output

$I_{s}+{\frac {V_{o}-V_{s}}{R_{3}}}=0,$ Kirchoff's current law

$V_{a}=V_{o}+{I_{s}}{R_{3}},$ rearranging to express $V_{a}$ in terms of $V_{o}$ and $I_{s}$

$V_{o}=V_{s}-{I_{s}}{R_{3}},$ rearranging to express $V_{o}$ in terms of $V_{s}$ and $I_{s}$

${\frac {V_{b}}{R_{1}}}+{\frac {V_{b}-V_{o}}{R_{2}}}=0,$ Kirchoff's current law

$V_{b}={\frac {{V_{o}}{R_{1}}}{R_{1}+R_{2}}},$ rearranging

$V_{o}=(V_{a}-V_{b})\alpha ,$ where $\alpha$= the opamp open loop gain

$(V_{o}+{I_{s}}{R_{3}}-{\frac {{V_{o}}{R_{1}}}{R_{1}+R_{2}}})\alpha =V_{o},$ substituting for $V_{a}$ and $V_{b}$

$\alpha {V_{o}}(1-{\frac {R_{1}}{R_{1}+R_{2}}})+\alpha {I_{s}}{R_{3}}=V_{o},$ rearranging

${V_{o}}(\alpha (1-{\frac {R_{1}}{R_{1}+R_{2}}})-1)=-\alpha {I_{s}}{R_{3}},$ rearranging

${V_{o}}(1-{\frac {R_{1}}{R_{1}+R_{2}}})=-{I_{s}}{R_{3}},$ cancelling out the $\alpha$ term and simplifying

$V_{o}=V_{s}-{I_{s}}{R_{3}},$ shown earlier

$V_{s}(1-{\frac {R_{1}}{R_{1}+R_{2}}})-{I_{s}}{R_{3}}(1-{\frac {R_{1}}{R_{1}+R_{2}}})+{I_{s}}{R_{3}}=0,$ substituting for $V_{o}$

$V_{s}({\frac {R_{2}}{R_{1}+R_{2}}})=-{I_{s}}{R_{3}}({\frac {R_{1}}{R_{1}+R_{2}}})),$

${\frac {V_{s}}{I_{s}}}=-{\frac {{R_{3}}{R_{1}}}{R_{2}}}$