User:Debosley
Italic textRubber Elasticity Revisited new article content ... 12/16/11
The commonly encountered theory of rubber elasticity suffers from an awkward disagreement with observation and some internal inconsistencies. These seem to arise from careless treatment of mathematics rather than weakness in the theory itself. As the rubber industry developed prior to theory, this is only of academic interest, but of interest all the same.
Rubber elasticity refers to the ability of high polymers to recover their shape after fairly large deformation as exemplified by a rubber band, not to the complete recovery from small deformation as with a quartz spring, and arises from entropy effects, concepts developed in the study of thermodynamics (heat + motion). (Treloar, L.R.G., "The Physics of Rubber Elasticity," Oxford, 1975.) Basic thermodynamic concepts and terminology were developed along with invention of the steam engine and provide a useful context for comparing rubber behavior.
One of the first discoveries was the mechanical equivalent of heat--that heat (q) was a form of energy--in fact, the kinetic energy of motion of the particles of matter. In gases, which dominate thermodynamic studies, it is translational motion, a defining property of an "ideal gas." A parallel discovery was that while mechanical energy could be (and usually was) converted entirely to heat, the reverse, conversion of heat to work (w), required special circumstances.
This kinetic theory of heat implied that if a hotter gas was placed next to a cooler gas, its faster moving molecules could drive an engine as they moved into the domain of slower ones, while the opposite was impossible. That is, a temperature difference was required to convert heat to work, and, in the process, temperatures tended to level out, at which point no more work could be extracted. At higher temperature there are more possible energy levels (velocities) among which the gas molecules can be arranged than at lower temperature. Calling this number of possible arrangements N, a property called entropy (symbol S) was defined as S = k ln N (k being Boltzmann’s constant). N is also proportional to the probability of the particular arrangement. Temperature (T), the degree (intensity) rather than the amount of heat, is somewhat circularly defined as proportional to the product, pv, of an ideal gas, in the units chosen for the constant R. With that definition S = q/T.
These concepts make up the famous two laws of thermodynamics. The first law assumes that heat and work make up an internal energy (E) such that dE = dq + dw: a change in the energy of a system is made up of heat (q) added to or removed from it and work (w) done on or by it. Energy is conserved. (Other types of energy such as chemical, electrical, etc., can be safely ignored here.) The equilibrating tendency of temperature that limits the amount of heat that can be converted to work led to the second law, where the probabilistic aspects of temperature were incorporated into the concept of entropy (as the ratio dS = dq/T), so that dE = TdS + dw.
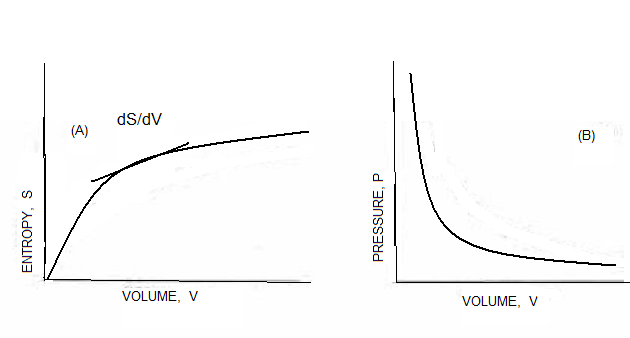
These concepts agreed nicely with the behavior of gases, where the separation and independence of actual molecules over a wide range of conditions closely approximates the theoretical (ideal-gas) model. Thus one can imagine a totally compressed array of molecules having only one arrangement (zero entropy) and imagine the array expanding isothermally (with heat supplied from some external reservoir) and becoming capable of an enormous number of arrangements (large entropy). If enclosed in a cylinder/piston, the expansion can convert some of the heat energy into mechanical work (dw = pdV) so that the first and second laws become dE = TdS – pdV (work done by the system on the surroundings is negative. In an ideal gas, energy doesn’t change with volume, hence p = T(dS/dV). (Figure 1)
The same considerations underlie the theory of rubber elasticity, though the details are more complex and seem to have created some difficulties. Rather than an assembly of structureless particles in random translational motion, the model is an assembly of structureless particles (mers) connected by rigid linkages at joints that allow for free rotation about the connections—a flexible chain (poly-mer), which can assume various shapes (iso-mers). Rather than translational motion, thermal (kinetic) energy causes the particles to rotate randomly about their linkages. Given their covalent bonding and structural complexity, no actual substances behave as “ideal rubbers.” Natural rubber, such as a common rubber band at room temperature, is about as near as it gets and is a good substance to experiment with.
Instead of the containing cylinder imagined for the ideal gas to measure pressure/volume, it is necessary to imagine some sort of clamp at each end of the chain capable of measuring force and displacement. As the (many) particles rotate about their neighbors and the shape of the chain changes, the ends will tend to move farther apart or closer together and exert a corresponding impulse (force) on the clamps. A particular end-to-end distance (r) may be compatible with a large number of rotational isomers or arrangements of the individual linkages. The ratio of that number to the total number of all arrangements for all possible end-to-end distances is the probability of that end-to-end distance.
Experimentally measurements or force and displacement are approximated with a macroscopic specimen and a stress-strain tester. As the time average of a member of an ensemble is the same as the ensemble average of a large number of individual members at any particular time, i.e., in a bulk sample, the values can be associated with the constituent molecular chains.
Corresponding to the second-law expression for gases (dE = TdS – pdV), for the one-dimensional rubber model it becomes dE = TdS + fdr. The force generally referred to is externally imposed and does work on the system, hence fdr is positive. Both pressure and force increase with temperature. Just as gases can be used to convert some heat to work, so stretched rubber can convert heat into mechanical motion. Google gives some two million references to “rubber heat engine.”
An accepted way of estimating the probability of end-to-end distances of polymer chains is based on the three-dimensional “random walk,” where, beginning at some point (usually taken as the origin of Cartesian axes), a point is moved some arbitrary (usually constant) distance in a “random” direction, i.e., independent of the direction of prior moves. After a (large) number, n, of steps of length, l, the probability of ending in a volume element dx dy dz about some point x, y, z, is
(deb: in case it appeals here is the superscripted exp() form, with integral signs: )
** P(x,y,z) dxdydz = (b3/pi3/2)exp(-b2(x2+y2+z2)) dxdydz **
where , which, along with the make all probabilities sum to unity. If every step were in the same direction, it would correspond to a fully extended chain. The equations mathematically allow infinite distances.
As positive and negative values of x, y, and z are equally likely, the average ending location of a large number of such walks tends to 0,0,0. This has sometimes got confused with the most probable value. The rubber-elasticity model is not concerned with the location in three-dimensional space of the “other” end but with the distance between the ends, and a distance cannot be negative. It is further concerned with the force, a vector, that is sensed by the imaginary clamps and necessarily directed along the line between them (between the ends of the molecule). There is no component of such force in any other direction.
These conditions can best be expressed in spherical coordinates. The coordinate, r, cannot be negative, and directional dependence can be removed by integrating the volume element over all values of the angular coordinates to get a volume element of ** 4πr2dr.** . As ** r2 = x 2+y2+z2,** ,
the probability expression reflecting that the “other” end is a distance r from the beginning (origin) is
** P(r)dr = (b3/pi3/2)exp(-b2r2)4pir2dr **
Differentiation with respect to r shows a maximum at r=1/b. The exponential term reflects a decrease with distance and the quadratic term reflects that the volume available to the “other” end is zero at the origin. An individual walk is not likely to end up where it started.
The corresponding expression for entropy, S, also maximum at r=1/b, is.
** S = k ln N ≈ k’lnP = k’(2lnr – b2r2)**
- ≈
Estimating N or P involves several approximations, particularly at extremes, so the functions differ in detail (Fig. 2(A) represents a sort of hybrid). The important point for this discussion is that there is some most probable value and it must be at the same end-to-end distance as for maximum entropy. As there is at least one arrangement (conformation) satisfying any r, S≥0.
- Force (f) = -TdS/dr = -2Tk’(1/r – b2r) **
and is zero at the most probable r = 1/b as expected.
A sketch of this relation resembles the force-extension relation of bulk rubber (Fig. 2). For various reasons, most treatments somehow ignore the quadratic (volume-element) term, making S maximum at r=0 and hence
** f = k”Tb2r, **
i.e., that the force acting between the ends of the chain is zero when the ends are coincident (r = 0). As r cannot be negative, this does not allow force to change sign. In particular, if the entropy function, S=f(r), has a maximum, which it does, then the slope, dS/dr = force necessarily has both positive and negative values.
Entropy cannot be maximum both at r=0 and r=1/b. Much of what follows is an attempt to identify the origin of this inconsistency. It draws on the Treloar text, using its terminology and equations (designated T). Most of the results seem to arise from using rectangular coordinates. Thus Treloar’s text gives the entropy of the chain as
s = k{ln p(x,y,z) dτ} =k{ln p(x,y,z)dx dy dz} (Eq. T3. T17)
as dτ has been defined as dx dy dz. Substituting from Eq. T3.5 yields
s = k{ln (constant) –b2r2 +ln dτ} (Eq. T3.18)
- (Eq. T3.18)
However changing the probability density from p(x,y,z) to p(r) requires changing the volume element from dτ (=dx dy dz) to 4πr2 dr, which is not a constant and
introduces the term 2ln r. Eq. T3.10 gives the most probable r = 1/b, which is not zero, while according to Eq. T3.19, S is maximum at r = 0. The contradiction results from using the rectangular volume element in spherical coordinates.
As a further example, Hill [Ref. Hill, T. L., Introduction to Statistical Thermodynamics, Addison Wesley, Reading, Mass., 1960.] writes of a flexible chain model, “The ends of the chain are a distance l apart and are on the x-axis. If the left end of the chain is considered fixed, we want to calculate … the equilibrium force tau along the x-axis necessary to hold the chain extended a distance l.” Then later, having found force to be zero for zero distance, he writes, “which is what we should expect on symmetry grounds (l can be positive or negative).” A negative l, however, puts the right-hand end to the left of the left-hand end--an impossibility.
The confusion arises from “symmetry grounds.” Both force and displacement changing sign at the origin simply replaces y = kx with –y = -kx--mathematically the same. It is much like saying (correctly) that the force is always zero, a fact one can demonstrate by stretching a rubber band and noting that it does not accelerate with respect to the fixed stars--hence f = ma = 0 by Newton’s second law. But the situation is not symmetric. The force is a vector and must have a feather end and an arrow end. If one lets go of one end of a stretched rubber band, it will accelerate, satisfying Newton, and define a vector direction. The direction is an arbitrary choice, but once a choice is made the other direction is excluded. The right-hand end stays to the right. Usual treatments assign positive force to external tensile force in the same direction as extensional displacement, not to the internal (symmetrical) retractive force.
Another contribution to the difficulty seems to arise from visualizing the rubber specimen as a filament, which cannot easily be deformed in (axial) compression but is handily stretched in a laboratory tensile tester. In real-world usage, most rubber has “changed sign” and is in (linear) compression: billions of tires, shoe soles, shock mounts and driven golf balls. The natives Columbus observed were bouncing, not stretching, rubber balls. One can draw grid lines on a large specimen, such as an eraser (rubber, hence the name) and observe this compression by bending it. Careful examination of bent fibers, though difficult, would show both extension and compression about a neutral axis.
The obvious occurrence of uniaxial compression in bulk rubber has forced attempts of reconciliation with the molecular model. Treloar posits the existence of a network where individual chains, having assumed equilibrium conformation, get connected by (mostly) tetravalent crosslinks, each segment between crosslinks becoming a molecular chain. As the ends cannot be coincident, every such segment must be in tension in that model. “This contractile tendency is counterbalanced by mutual repulsive forces between the atoms.” Such model is not structureless and introduces an energy component to force and so cannot be compared with the entropic model. Rubber filaments crystallized under strain actually grow longer (force changes sign) (Ref. Smith, W.H., and C.P. Saylor. J. Res. Natl. Bur. Stds., 21, 257, (1938)), which is difficult to reconcile with the contractile model.
Many treatments include a more sophisticated analysis that leads to a force-extension relation involving the inverse Langevin function. This is appealing, as the Langevin function applies to balancing alignment of dipoles against randomizing thermal-agitation forces, similar to aligning chain segments against thermal motion. Dipoles are independent while chain segments are connected, and the derivations are not altogether clear. Hill’s treatment (above, with the left right-hand end) leads to this function. At any rate, the Langevin function is zero at r=0 and approaches the Gaussian at small r, so it also does not allow force to change sign.
link to picture:
!-- EDIT BELOW THIS LINE -->
- Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "http://localhost:6011/en.wiki.x.io/v1/":): {\displaystyle S=klnN≈k' lnP = k'(2lnr - b^2r^2) \,}



















