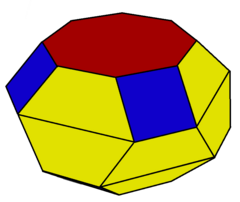
Truncated square antiprism

Truncated square antiprism
Type	Truncated antiprism
Schläfli symbol	ts{2,8} tsr{4,2} or $ts{\begin{Bmatrix}4\\2\end{Bmatrix}}$
Conway notation	tA4
Faces	18: 2 {8}, 8 {6}, 8 {4}
Edges	48
Vertices	32
Symmetry group	D4d, [2+,8], (2*4), order 16
Rotation group	D4, [2,4]+, (224), order 8
Dual polyhedron
Properties	convex, zonohedron

The truncated square antiprism one in an infinite series of truncated antiprisms, constructed as a truncated square antiprism. It has 18 faces, 2 octagons, 8 hexagons, and 8 squares.

Gyroelongated triamond square bicupola

If the hexagons are folded, it can be constructed by regular polygons. Or each folded hexagon can be replaced by two triamonds, adding 8 edges (56), and 4 faces (32). This form is called a gyroelongated triamond square bicupola.

Related polyhedra

Truncated antiprisms

Symmetry	D2d, [2+,4], (2*2)	D3d, [2+,6], (2*3)	D4d, [2+,8], (2*4)	D5d, [2+,10], (2*5)
Antiprisms	s{2,4} (v:4; e:8; f:6)	s{2,6} (v:6; e:12; f:8)	s{2,8} (v:8; e:16; f:10)	s{2,10} (v:10; e:20; f:12)
Truncated antiprisms	ts{2,4} (v:16;e:24;f:10)	ts{2,6} (v:24; e:36; f:14)	ts{2,8} (v:32; e:48; f:18)	ts{2,10} (v:40; e:60; f:22)

Snub square antiprism

Although it can't be made by all regular planar faces, its alternation is the Johnson solid, the snub square antiprism.

References

• Snub Anti-Prisms