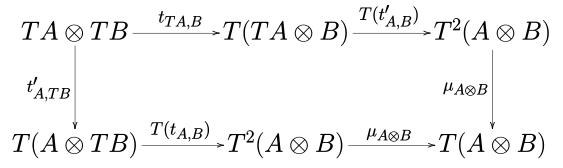Talk:Strong monad

This article was nominated for deletion on 16 July 2024. The result of the discussion was keep.

This article is within the scope of WikiProject Computer science, a collaborative effort to improve the coverage of Computer science related articles on Wikipedia. If you would like to participate, please visit the project page, where you can join the discussion and see a list of open tasks.Computer scienceWikipedia:WikiProject Computer scienceTemplate:WikiProject Computer scienceComputer science

Low

This article has been rated as Low-importance on the project's importance scale.

Things you can help WikiProject Computer science with:

Here are some tasks awaiting attention:

Article requests :
- Requested articles/Applied arts and sciences/Computer science, computing, and Internet
Cleanup :
- Computer science articles needing attention
- Computer science articles needing expert attention
Copyedit :
- Computing
Expand :
- Computer science
Infobox :
- Computer science articles without infoboxes
Maintain :
- Timeline of computing 2020–present
Photo :
- Find pictures for the biographies of computer scientists (see List of computer scientists)
- Computing articles needing images
Stubs :
- Computer science stubs
Unreferenced :
- WikiProject Computer science/Unreferenced BLPs
Project-related :
- Tag all relevant articles in Category:Computer science and sub-categories with {{WikiProject Computer science}}

The notation $\gamma _{A,B}$ is not explained. I think it should be explained as the linked page symmetric monoidal category uses a different notation.Bandanna (talk) 11:36, 23 May 2019 (UTC)[reply]

I don't know how to generate a diagram in png, but the first one should be corrected. There is \lambda_A but should be \lambda_{T A}. -- Good point. I have corrected this mistake.--IkamusumeFan (talk) 08:06, 14 November 2014 (UTC)[reply]

What are strong monads good for? This article doesn't say. Please, someone, give a theorem that justifies the definition. John Baez (talk) 12:00, 19 July 2009 (UTC)[reply]

I replied to this question in a new version of the page: strong monads are good at modelling side effects in computer science, because their Kleisli categories are premonoidal in a canonical way. Alexis.Toumi (talk) 09:41, 22 October 2024 (UTC)[reply]

I concur, should add something about how strong monads are strong lax monoidal functors wrt cartesian product, providing the appropriate tensorial strength, and so lead to a popular belief (in comp sci) that all monads are "applicative functors" (see, e.g. strictlypositive.org/IdiomLite.pdf Vlad Patryshev (talk) 01:50, 11 January 2012 (UTC)[reply]

Diagram Simplification

For any commutative strong monad, the following two diagrams are essentially the same.

,

--IkamusumeFan (talk) 08:06, 14 November 2014 (UTC)[reply]

The first diagram implies the second, but the second does not imply the first. — Preceding unsigned comment added by 58.3.145.109 (talk) 01:20, 8 January 2015 (UTC)[reply]

It was my fault. They are not identical indeed. --IkamusumeFan (talk) 20:42, 19 April 2015 (UTC)[reply]

Commutative strong monad

I think the diagram for the commutativity is false. See http://home.math.au.dk/kock/MSMCC.pdf definition 3.1. — Preceding unsigned comment added by Barth Shiki (talk • contribs) 12:31, 10 March 2015 (UTC)[reply]

OK I didn't see the discussion above. As it is said the two are not equivalent and the previous version was the original definition. Besides, with the current definition, the remark on symmetric monoidal monads seems doubtful. — Preceding unsigned comment added by Barth Shiki (talk • contribs) 19:21, 10 March 2015 (UTC)[reply]

I have corrected the error. Also a paper has been found to support the points. --IkamusumeFan (talk) 20:42, 19 April 2015 (UTC)[reply]