Talk:Pythagorean theorem/Archive 6
| This is an archive of past discussions about Pythagorean theorem. Do not edit the contents of this page. If you wish to start a new discussion or revive an old one, please do so on the current talk page. |
| Archive 1 | ← | Archive 4 | Archive 5 | Archive 6 | Archive 7 |
Dijkstra generalization as subsection 9.10 of main article
In Euclidean geometry, Pythagoras' Theorem holds for any three points A, B and C such that through A and C a straight line can be drawn orthogonal to a straight line through B and C. How many mathematicians appreciate that the theorem remains applicable when some or all of the points A, B and C coincide? it is widely used all over the world.also ,it is a good tool to help with the problems about Shortest Path!
Yet this seems largely responsible for the convenience with which Pythagoras theorem can be used:
- Edsger W. DIJKSTRA. "Notes on Structured Programming". p. 3 month = apr, year = "1970", note = "circulated privately", url = "http://www.cs.utexas.edu/users/EWD/ewd02xx/EWD249.PDF".
— Preceding unsigned comment added by NemoNF (talk • contribs) 05:11, 9 October 2011
History of the Theorem in the introduction
Right now the paragraph on the history of the theorem in the Introduction reads:
- Indented line The Pythagorean theorem is named after the Greek mathematician Pythagoras, who by tradition is credited with its discovery and proof,[2][3] although it is often argued that knowledge of the theorem predates him. There is evidence that Babylonian mathematicians understood the formula, although there is little surviving evidence that they fitted it into a mathematical framework.[4][5]
I suggest that we change it to:
- Indented line The Pythagorean theorem is named after the Greek mathematician Pythagoras, who by tradition is credited with its discovery and proof,[2][3] although it is often argued that knowledge of the theorem predates him. References to Pythagorean triples, and to the theorem, have been found in ancient texts from Babylon, China and India.
In its current form, the introductions seems to go into the detail of only one of the other possible sources of the theorem, though all three sources listed in the History section (Babylonian list of triples, Zhou Bi Suan Jing, and the Apastamba Shulba Sutras) are claimed to predate Pythagoras. Mentioning only Pythagoras and Babylon therefore sounds (at least to me) mildly POV (unless of course the claims in the History section can be challenged, but they appear to be properly sourced). Piyush (talk) 23:43, 4 December 2011 (UTC)
- It's not clear that the others predate Pythagoras: the dates for each is much vaguer, raging from before to after his dates, so there's no evidence for them actually predating him. Even if they were there's no evidence that knowledge spread to Greece. The Babylonian tablets are much earlier and there's evidence that much of their maths was preserved through the Greeks: for example we are thought to have 360 degrees in a full turn and 60 minutes in the hour because of them. The article does suggest the theory reached India from Babylon (there's a lengthy quote in the ref), but I don't know how likely that is.--JohnBlackburnewordsdeeds 01:33, 5 December 2011 (UTC)
The lengthy quote also does not give any evidence for why it is more likely that it would have reached India from Babylon, or if indeed it is likely at all. On the other hand, the article on Shulba Sutras includes a citation to Plofker, which attributes the appearance to the Baudhayana Shulba Sutras, and dates them to 800-600BC (which is before the time of Pythagoras), supposedly on linguistic evidence. I am not an expert, so I wouldn't know which to give more weight. What I find puzzling is the lack of primary sources: both of the above two quotes (Boyer and Plofker) seem to pulling data out if thin air (Mesopotamian influence on Shulba Sutras for Boyer and dates for the Shulba Sutras in the latter). Tongue firmly in cheek, I would like to suggest they might have their own opposing POVs. Piyush (talk) 05:52, 6 December 2011 (UTC)
I just notied another curious (but referenced) statement in the article: "According to Albert Bŭrk, this is the original proof of the theorem; he further theorizes that Pythagoras visited Arakonam, India, and copied it." Looks like there is a lot of assertion without evidence (or on lousy evidence) going on in the field of the history of Pythagoras theorem, so I guess I had better leave it alone till the historians figure out whether the Indians copied it from the Mesopotamians, or the Greeks copied it from the Indians and the Mesopotamians. Piyush (talk) 06:00, 6 December 2011 (UTC)
- Why do you say it's referenced? Finding no source, I removed it. Dicklyon (talk) 06:06, 6 December 2011 (UTC)
- Yes, I just noticed the statement was not sourced. However, a quick Google search reveals this reference. That reference also dates the statements in both the Baudhayan and Apastamba Sulba Sutras to 800BCE and 600BCE respectively. I am not adding these in now, but I think some restructuring of the treatment of the history of the theorem seems warranted, especially in light of the fact that all sources seem to date both Baudhayan and Apatamba before Pythagoras, contrary to the claims that these dates are "disputed". Piyush (talk) 15:29, 6 December 2011 (UTC)
- Also, there seems to be some confusion about Shulba Sutras: my reading of the references seems to be that there are many of them, dated between 800BCE and 200CE, but the ones most relevant to this article (Baudhayana and Apastamba) are among the oldest and date between 800BCE and 600BCE. Piyush (talk) 15:31, 6 December 2011 (UTC)
- One more point: I thing in spite of the reference being available, we should leave out Albert Burk's statement, since it seems to be not well accepted. I am also not sure about Boyer's claim of Mesopotamian origin though: that seems disputed too, and the only reason Boyer gives is that the triplets are the same as those given in Babylonian texts. That doesn't look like a reason to impute origin at all, since it is equally likely that the writers of the Shulba Sutras and the Babylonians hit upon the same rule. But before deciding on removing it, we probably need reference which either raise these objections or give support for Boyer's claim of Babylonian origin. Piyush (talk) 15:39, 6 December 2011 (UTC)
- Yes, I just noticed the statement was not sourced. However, a quick Google search reveals this reference. That reference also dates the statements in both the Baudhayan and Apastamba Sulba Sutras to 800BCE and 600BCE respectively. I am not adding these in now, but I think some restructuring of the treatment of the history of the theorem seems warranted, especially in light of the fact that all sources seem to date both Baudhayan and Apatamba before Pythagoras, contrary to the claims that these dates are "disputed". Piyush (talk) 15:29, 6 December 2011 (UTC)
copyright issue
From the link posted above it seems the history section was in large part copied from that source with minor rearrangements (possibly done by editors since). The problem is too large to be easily fixed so I've blanked the section. It can be reintroduced if someone spends the time rewriting pretty much all of it to avoid the copyright violations, though even then it would suffer from being based on a single source.--JohnBlackburnewordsdeeds 15:43, 6 December 2011 (UTC)
- mea culpa, it seems there's not a copyright problem. The book was published in 2007, I've checked the page history and the history section is at least that old. The book is copied from Wikipedia, i.e. it used this article as a very close source. So it is certainly not a valuable source here, per WP:CIRCULAR. First time I've had to write that about a print publication !--JohnBlackburnewordsdeeds 15:54, 6 December 2011 (UTC)
Another pop reference
There's another pop culture reference for the section Pop references to the Pythagorean theorem
Private from The Penguins of Madagascar quotes "The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side." in the 6th episode of season 1, namely "Paternal Egg-Stinct".
Well, maybe it's actually more a reference to the Wizzard of Oz. --Siteswapper (talk) 18:45, 19 March 2012 (UTC)
Changing notations explanation
Regarding [revision]. Changed notation to only uppercase and accordingly the image so that the format is more consistent. Per comments at Wikipedia:Featured_picture_candidates/Pythagoras_similar_triangles_proof.--Gauravjuvekar (talk) 10:43, 15 May 2012 (UTC)
"Proof" by Rearrangement
This is not a proof by any standard. The animation is ok for getting an intuition as to why the theorem should hold, but it does not prove the theorem. — Preceding unsigned comment added by 2.29.149.104 (talk) 21:57, 29 July 2012 (UTC)
- It is a form of geometric proof, i.e. a more intuitive proof than a formal algebraic one. As such it's useful to help people understand the theorem, or to convince people without resorting to advanced techniques they may not know. But geometric proofs can also be formalised, or used as the basis for a formal proof. In particular the proof from Euclid's elements is very much a geometric proof, but done formally.--JohnBlackburnewordsdeeds 22:08, 29 July 2012 (UTC)
- To me, Pythagorean tiling provides the best informal proof, like the drawing (the app at the top) demonstrates here: both the large square and the two smaller ones together will tile the whole plane, no animation or calculations necessary. Just my personal preference. Ssscienccce (talk) 05:08, 25 September 2012 (UTC)
New 'Through a tiling pattern' section
Although this was well meant and I think contained some valuable content I have removed it because it had a number of issues. The main one was the content in full was
Whatever the ratio of sizes of square elements, their total area a 2 + b 2 equals the area of a square pattern: c 2. In other words, for any shape of right triangle, the square of the hypotenuse equals the sum of squares of the legs. With the hypotenuse length as length unit, the equality becomes: sin 2 θ + cos 2 θ = 1.
Which makes no sense. It seemed to follow on from the captions but the article should make sense on its own, without the images and captions which are there primarily for illustration. Images are more important in an article about geometry but they are not part of the article text. At the same time the images and captions contain far too much information, with in particular the images confusing and difficult to make sense of. There are too many images, there probably only needs to be one purely geometric one. And the mathematical content quoted above and the images includes far more mathematical content than it needs, i.e. a restatement of the theorem and trigonometric content. Finally there are minor formatting and style issues, such as excessive spacing.
This could probably all be fixed, but given the problems I have removed the section.--JohnBlackburnewordsdeeds 11:46, 12 October 2012 (UTC)
- It's hard to tell, but maybe this is trying to be a reference to Pythagorean tiling? —David Eppstein (talk) 16:26, 12 October 2012 (UTC)
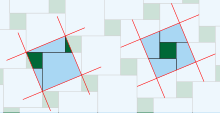
- Yes, I thought of that thinking what to do with it. Pythagorean tiling can be used to do another rearrangement proof: two possible ones are obvious from this diagram, from that article and far better than any of those just added. The problem is with three images there already it would take some rearrangement of the article to fit it in, and I got distracted before trying to anything about it. Alternately just a link to Pythagorean tiling with a sentence – the article's already very long and we can't include every proof, especially not ones covered elsewhere.--JohnBlackburnewordsdeeds 16:44, 12 October 2012 (UTC)
There are literally hundreds of proofs of the Pythagorean theorem due, in part, to a standard question on Cambridge's infamous Tripos exam which asked for a novel proof of the result. With that background, it is unlikely that this is really a new proof, but I am getting the impression that the editor may have come up with this rearrangement proof on his/her own (hence the vigorous defense of its inclusion.) I would then claim that this is a violation of WP:NOR, even given the remote chance that the editor could come up with a reliable reference for this proof, and so, not appropriate for Wikipedia. Bill Cherowitzo (talk) 16:49, 13 October 2012 (UTC)
-
Here is the only proof by rearrangement on the current article without this error: the omission of the particular case of an isosceles right triangle.
— Aughost (talk) 19:14, 13 October 2012 (UTC)- What 'error' ? None of the proofs are perfect; in particular some are more geometric and intuitive but less rigorous, others are more formal but less accessible. But none are wrong that I can see, and if they were the correct thing to do is to fix any error(s).
- And that deals with none of the objections raised above and in the edit summaries to your addition. It is still very badly formatted and presented, with numerous style problems, confusing graphics and is much too large for the article. The article is already long and not short of proofs, so it is best to remove these while they have so many problems and disrupt the article so badly.--JohnBlackburnewordsdeeds 19:45, 13 October 2012 (UTC)
Tiling
No link to "Pythagorean tiling" on the current article, no occurrence of these words: "tiling", "tessellation". However, we read on this talk page this: "To me, Pythagorean tiling provides the best informal proof", or that: "It's hard to tell, but maybe this is trying to be a reference to Pythagorean tiling". The idea of tiling is it taboo for the main authors? 109.6.129.249 (talk) 14:46, 17 October 2012 (UTC)
- Easily fixed. I have added a link to Pythagorean tiling in the "See Also" section. Gandalf61 (talk) 15:08, 17 October 2012 (UTC)
- Thank you. 109.6.129.249 (talk) 15:58, 17 October 2012 (UTC)
Pythagoras in 3 or more dimensions
- It seems to me that Pythagoras's theorem breaks down where there are 3 or more dimensions (e.g. the complex plane, with 4 dimensions: x, ix, ix, iy), because all proofs of Pythagoras's theorem depend on adding and subtracting areas, and all these areas and their corners must be in the same plane for this addition and subtraction to work, and this does not happen in the complex plane with points separated in varying combinations of the 4 dimensions x, ix, ix, iy. Anthony Appleyard (talk) 09:15, 7 November 2012 (UTC)

- You can do it recursively. Using the figure on the right, where the lengths of the sides are a, b, c and length of the diagonal is d. First find the distance BD using 2D Pythagoras on triangle BCD. We now have a right angle triangle ABD and length AD is . The same sort of argument can be extended to higher dimensions.--Salix (talk): 09:53, 7 November 2012 (UTC)
Dates for Āpastamba Sulba Sutra
In this article, the date for the Apastamba Sulba Sutra is given as "ca. 600 BC". In the reference page for the Apastamba Sutra [1], however, it is given as approximately "between 450-350 BC". — Preceding unsigned comment added by TheLastPaladin (talk • contribs) 03:49, 31 March 2013 (UTC)
- As I understand it, these Sulba Sutras are extremely hard to date as they contain no internal clues as to when they were written. Different historians give wildly different dates based on, what I would consider, very weak inferences. The 600 BC date seems to come from van der Waerden (although the article doesn't quite say this) and the 450-350 BC is due to someone called Kane, who appears to be some type of authority, but is not referenced in that article. Wikipedia is not the place to settle these academic disputes, but we should do a better job of indicating who said what. Bill Cherowitzo (talk) 04:35, 31 March 2013 (UTC)
Computer proofs of Euclid theorems
The proof by similar triangles, was produced by a computer program set to check Euclid. This proof was ignored by the president of the IMA in an article on proofs of Pythagoras!
The first new proof was: Isosceles triangles have equal base angles. It was as follows; Let the triangle be RLT with TR = TL. TRL and TLR are congruent!
Sorry, I have not the references to hand, but I first heard about it in the '70s Bparslow (talk) 10:58, 4 May 2013 (UTC)
How did the theorem get its name?
How did the Pythagorean theorem get its name? Is it named after someone? -ErinHowarth (talk) 18:46, 23 May 2013 (UTC)
- Look at the penultimate (next to last) paragraph of the History section of this article. This is about the best you can hope for in answer to your first question, and yes, it is named after someone. Bill Cherowitzo (talk) 19:42, 23 May 2013 (UTC)
- It is named after Pythagoras.--Mr.23 (talk) 23:50, 28 May 2013 (UTC)
Citation needed
There is a citation needed tag at the end of the "Inner product spaces" section. Can someone check this out? --FutureTrillionaire (talk) 02:59, 5 July 2013 (UTC)
- I went ahead and removed it.--FutureTrillionaire (talk) 12:56, 5 July 2013 (UTC)
- This paper [2] could be used as a reference to the fact of Parseval's identity being a generalisation of Pythagoras.--Salix (talk): 18:26, 5 July 2013 (UTC)
My edits
I did three main things.
First, I think the Geometry template is plenty, so I removed the Trigonometry template. Notice that the article's hatnote says "See also: Pythagorean trigonometric identity". So, the Trigonometry template can go there. Here, the Trigonometry template went so far down the article that it would bump up against other images.
Second, in the lead, I don't think the theorem ought to be introduced just as a relationship of areas. The top figure makes that connection which is fine and sufficient. The theorem has always been most useful for calculating one side of a right angle when you know the other two sides, and it's much rarer that anyone cares about the areas of squares that are attached to a triangle.
Third, I inserted a new subsection explaining the proof that is attributed to Pythagoras. This proof is so extremely simple and brief, that it ought to be presented up front. The other proofs described later in the article are fine, but this one needs to come first, in my opinion. So, we start by presenting the main form of the theorem, and the main proof of the theorem. Other forms and other proofs appropriately come later. Cheers,Anythingyouwant (talk) 08:07, 30 August 2013 (UTC)
American Indian joke
Should the popular joke with the punchline "the squaw of the hippopotamus is equal to the sum of the squaws of the hides" be included in the Popular Culture references? — Preceding unsigned comment added by 108.225.17.141 (talk) 08:39, 2 October 2013 (UTC)
- It might fit better in a new "further generalisations and conjectures" section. Tkuvho (talk) 10:25, 2 October 2013 (UTC)
application
Need section on application s, if any. Put on mobile version too.--IronMaidenRocks (talk) 07:33, 12 March 2014 (UTC)
algebraic formula for the pythagorean theorem
Bhaskara came up with the original theorem (or so I have been told) and his name is not listed. Instead garfield's name is listed with a theorem that came 1000 years later. — Preceding unsigned comment added by Eddiec005 (talk • contribs) 17:19, 18 March 2014 (UTC)
- Do you have some more information, or a source? There's more than one mathematician called Bhāskara so it's unclear even who you mean.--JohnBlackburnewordsdeeds 17:52, 18 March 2014 (UTC)
Semi-protected edit request on 29 March : please add the following text+picture to the end of section "Pythagorean triples" in chapter "Consequences and uses of the theorem". Thank you.
This edit request has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
All primitive Pythagorean triples are geometrically interconnected, starting with the first triple (3, 4, 5) which revolves around a central square of side 1. For example, below is shown the geometric relation of the sequence of odd triples of Pythagoras, i.e.
(3, 4, 5), (5, 12, 13), (7, 24, 25), (9, 40, 41)

Celdomi (talk) 23:18, 29 March 2014 (UTC)
- I'm skeptical that this is an improvement. For one thing, the text is incorrect: it does not include all primitive triples (e.g. where is 8,15,17?). For another, its construction appears to be original research. —David Eppstein (talk) 23:27, 29 March 2014 (UTC)
Celdomi (talk) 20:34, 31 March 2014 (UTC)
- Hello David. The triple (8, 15, 17) belongs to the even sequence of triples which is presented geometrically in the same manner. Please refer to the new Figure annexed below.

Each geometrical construction represents a branch of the tree of primitive Pythagorean triples.
These two geometrical constructions are explained in more detailed in the Wikipedia webpage Geometry of the Pythagorean Triples
 Not done: please establish a consensus for this alteration before using the
Not done: please establish a consensus for this alteration before using the {{edit semi-protected}}template. — {{U|Technical 13}} (t • e • c) 02:12, 2 April 2014 (UTC)
Celdomi (talk) 21:57, 2 April 2014 (UTC) Sorry, there was a mistake in the last link. Here it is again: Geometry of the Pythagorean Triples.
 Not done: please establish a consensus for this alteration before using the
Not done: please establish a consensus for this alteration before using the {{edit semi-protected}}template. You still need a consensus to implement this requested change as there seems to be some disagreement as to whether or not this is an improvement. — {{U|Technical 13}} (t • e • c) 23:04, 2 April 2014 (UTC)
Celdomi (talk) 12:07, 3 April 2014 (UTC) Understood. I am new to this... do we continue the discussion here, or is there another way? @David: please send me your queries so we arrive to a consensus. Cheers.
- I don't think these help. They show there is a relationship between them but it's unclear what it is, and I can't find it in this article or any other obvious. It looks like a relationship between a cherry picked set of triples, a trivial consequence of something else like the tree of primitive Pythagorean triples, and so OR.--JohnBlackburnewordsdeeds 12:39, 3 April 2014 (UTC)
- I see no harm in adding these diagrams. The may be original but their veracity is not in doubt as they would count as routine calculations. Martin Hogbin (talk) 09:23, 14 June 2014 (UTC)
- Routine calculations is things like doing basic arithmetic, not constructing series of pythagorean triples. The series of triples can be sourced but the geometric relationship between them cannot and is original research. Images don't need sourcing but any text accompanying them does, and these would need text to explain as they are far from clear and straightforward. These are not about the theorem except in the loosest sense, containing many instances of the theorem but we already have lots of much clearer pictures of the theorem.

- Finally they are just badly drawn: you can make out the numbers in the far too big diagrams above but at the size they'd appear in the article as right they're unreadable. Not easily fixable as if all the numbers, letters and subscripts were of a readable size they'd hardly fit on.--JohnBlackburnewordsdeeds 11:49, 14 June 2014 (UTC)
- But what is required in WP is verifiability not plagiarism. We can, indeed should, use our own drawings to illustrate something that can be verified to be correct.
- I find the numbers perfectly readable. Martin Hogbin (talk) 18:44, 14 June 2014 (UTC)
- But except for the simplest arithmetic calculations we verify things from sources, and no source has been given for this geometric construction. Images don't need sourcing but text does, and this needs explaining as non-obvious. So where's the source? And I'd be very surprised if you can read the text on it at the size it appears in articles i.e. 220px as at right, they're impossible to read in some cases, certainly well beyond the limits of easy readability.
- It's also off-topic here. It's more relevant to an article about Pythagorean triples, such as Tree of primitive Pythagorean triples where the triples come from. But it's unsourced original research there too and has already been removed as such from there. It needs sourcing as a non-obvious, non-trivial geometric interpretation of Pythagorean triples. And a new image would be needed that's legible at 220px.--JohnBlackburnewordsdeeds 19:16, 14 June 2014 (UTC)
Semi-protected edit request on 26 June 2014
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
62.254.105.220 (talk) 10:58, 26 June 2014 (UTC)
 Not done: as you have not requested a change.
Not done: as you have not requested a change.
If you want to suggest a change, please request this in the form "Please replace XXX with YYY" or "Please add ZZZ between PPP and QQQ".
Please also cite reliable sources to back up your request, without which no information should be added to any article. - Arjayay (talk) 11:08, 26 June 2014 (UTC)
Semi-protected edit request on 5 July 2014
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
I wanted to suggest adding under the Section 8 "In Popular Culture" that in carpentry and construction the Pythagorean Theorem is sometimes called "The 3-4-5 Rule." See: http://www.wikihow.com/Use-the-3-4-5-Rule-to-Build-Square-Corners Timfoutz (talk) 15:05, 5 July 2014 (UTC)
Possessive S
Please, Cherkash, you're getting close to breaking the three revert rule now. The apostrophe after a name ending in "s" is, at best, a matter of personal style. From what I can see online, leaving the extra "s" off classical names tends toward the rule. As User:DVdm has pointed out, in the comments, an overwhelming majority of google hits suggest most people do not use an extra "s". It seems from your talk page that you are involved in another similar crusade at Bayes' theorem, and EdJohnston has tried to show you that the debate has long ago ended there as well. - TheMightyQuill (talk) 03:54, 30 July 2014 (UTC)
- Yes, let's keep it as it was before, i.e. "Pythagoras' theorem". The inititial change seems to lack consensus: "In discussions of proposals to add, modify or remove material in articles, a lack of consensus commonly results in retaining the version of the article as it was prior to the proposal or bold edit." I have warned user on their talk page. - DVdm (talk) 07:48, 30 July 2014 (UTC)
- This seems to be a fairly common discussion on Wiki. And unfortunately, the selectivity and bias in choosing which rules/policies to quote usually show editors' own preferences, rather than demonstrate a balanced approach. So let's get the facts straight: this was not the "initial change" – edits like this were happening back and forth throughout many years that this article existed. Why would you prefer to apply your policy of choice in the A->B but not in the B->A direction? (How about this change from 2008 for example? or any other in a bunch of similar changes on the pattern "s's"->"s' " that were done throughout the years? I don't believe there was a consensus reached – or even asked for – in each and every one of those cases.) So if you try to throw a book at me, at least get your facts straight.
- Now, to a more subtle point: is this policy even relevant? The policy that you chose to quote usually applies to controversial edits that involve an article's "material", "matter", "content", etc. It's rarely applied to the written form in itself that doesn't change the meaning (e.g. mis-spellings, incorrectly applied punctuation, etc. would be in this category) – and indeed, most grammatical, punctuational, and other similar errors are (and of course, should be) encouraged to be corrected without seeking consensus (see e.g. Wikipedia:Typo Team, Wikipedia:Basic copyediting, etc.).
- There are a few cases, especially around the grammar rules that happen to be widely misunderstood, which continuously cause editors to revert things after they've been corrected – and then trying to justify the reverts back to incorrect spelling and punctuation by doing google searches. The use of 's after singular nouns seems to be one of such cases.
- In the possessive apostrophe article, there's a clear guidance given on the standard modern English use, including analysis of various manuals of style. In particular, quoting: the so-called "standard principle" "recommend[s] that practically all singular nouns, including those ending with a sibilant sound, have possessive forms with an extra s after the apostrophe"; there's also a mention of the "older practice of omitting the extra s in all cases ending with a sibilant", where the practice is described for what it is – older, or in other words outdated. There are very limited exceptions, where indeed both forms are commonly acceptable (Jesus' or Jesus's) – but there are no examples where the "s's" form is incorrect and "s' " form is the one that is the only one acceptable.
- So in the spirit of seeking the widest possible consensus (if you still insist the matter is controversial – which I hope you do not by now, as it falls within standard copyediting practice), based on the analysis above I propose the "s's" form as the one that the smallest number of editors would find objectionable: there are no rules or manuals of style that call the "s's" form outright incorrect – whereas there are plenty that do so in case of "s' ". cherkash (talk) 01:13, 31 July 2014 (UTC)
- Indeed, "there are no rules or manuals of style that call the "s's" form outright incorrect", so it boils down to the rule—or rather, policy—of local wp:consensus as established on the talk page. As it is now, there is no consensus to make the change, so I propose we revert to the way it was. - DVdm (talk) 08:26, 31 July 2014 (UTC)
Semi-protected edit request on 15 December 2014
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
Change Pythagoras's theorem to Pythagoras' theorem because that is correct Mdabedin (talk) 00:59, 15 December 2014 (UTC)
 Not done: please provide reliable sources that support the change you want to be made. — {{U|Technical 13}} (e • t • c) 03:56, 15 December 2014 (UTC)
Not done: please provide reliable sources that support the change you want to be made. — {{U|Technical 13}} (e • t • c) 03:56, 15 December 2014 (UTC)
Other generalizations
I suggest that the following two new subsections be put into the section on generalizations. But I'm reluctant to put them in without illustrations, which I don't know how to create. Maybe an interested editor could create the images and put these in.
Isosceles triangle construction
In triangle ABC with opposite sides a, b, c and c > a, construct BD of length c with D on AC extended. Denote length CD = d. Then[1][2] The Pythagorean theorem is the case where ∠BCA = 90° so d = b.
Isosceles trapezoid construction
For triangle ABC, construct D and E such that DCE is parallel to AB with ∠CAD = ∠CBA and ∠CBE = ∠BAC. Denote lengths DC = d and CE = e. Then[3] The Pythagorean theorem is the case where ∠A + ∠B = 90° so d + e = c.
- ^ Hoehn, L., "A neglected Pythagorean-like formula", Mathematical Gazette 84, March 2000, 71-73.
- ^ Darvasi, G., "More notes on a neglected Pythagorean-like formula", Mathematical Gazette 85, November 2001, 483-486.
- ^ Hoehn, L., "A generalisation of Pythagoras' theorem", Mathematical Gazette 92, July 2008, 316-317.
Loraof (talk) 23:36, 16 December 2014 (UTC)
- I'd be reluctant to put them in. The theorem can be used in many different ways in geometry, and the article is already very long. So I think restricting it to obvious generalisations - higher dimensions, other shapes, other geometries - and to well known theorems such as the law of cosines makes sense. Otherwise there could be no end of theorems that are in some way a generalisation as they use it in some way.--JohnBlackburnewordsdeeds 00:00, 17 December 2014 (UTC)
Semi-protected edit request on 16 February 2015
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
5.234.157.79 (talk) 12:13, 16 February 2015 (UTC)
 Not done: it's not clear what changes you want to be made. Please mention the specific changes in a "change X to Y" format. Please re-open this request by changing answered=yes to answered=no and providing your request in the form of please change X to Y, providing any necessary sources. Thanks, NiciVampireHeart 12:19, 16 February 2015 (UTC)
Not done: it's not clear what changes you want to be made. Please mention the specific changes in a "change X to Y" format. Please re-open this request by changing answered=yes to answered=no and providing your request in the form of please change X to Y, providing any necessary sources. Thanks, NiciVampireHeart 12:19, 16 February 2015 (UTC)
Who?
Who disputes that the Pythagorean Theorem (if not its proof) was discovered before Pythagorus lived?Anythingyouwant (talk) 00:32, 9 March 2015 (UTC)
- Who do you claim discovered it? If your claim is based on Plimpton 322, there are multiple alternative explanations that do not involve right triangles and areas of squares on their sides; see the Plimpton 322 article for details. If it's based on the Shulba Sutras, then whether they were before or after Pythagoras is also questionable. If it's base on the Egyptian use of the 3-4-5 triangle, then that's not the theorem, it's just a single example of a right triangle and is divorced from the areas of the squares on its sides. So what is the basis of the claim that the theorem is pre-Pythagorean? —David Eppstein (talk) 01:45, 9 March 2015 (UTC)
- There are lots of sources that say the theorem was known earlier than Pythagorus (see, e.g. the Posamentier book linked in this Wikipedia article). Those reliable sources may well be wrong, as you suggest, but I am asking for a reliable source that says they are wrong. If no reliable source says so, then we are not supposed to write in the Wikipedia article that the matter is disputed. I am asking for a reliable source saying that it's disputed.Anythingyouwant (talk) 01:54, 9 March 2015 (UTC)
- If some reliable sources say one thing and some say others, we should not be choosing among them to pick what we want to say; we should be saying it is disputed. And if there is no undisputed predecessor of Pythagoras for this theorem, then clearly it is disputed. And your pointing to a popular-press oversimplification as a source when there is plenty of scholarly literature on this question is probably also not the best choice, at least by itself. —David Eppstein (talk) 02:36, 9 March 2015 (UTC)
- Please point to scholarly literature that says its disputed. We ought to cite it.Anythingyouwant (talk) 03:46, 9 March 2015 (UTC)
- You mean like Robson, Eleanor (2002), "Words and pictures: new light on Plimpton 322" (PDF), American Mathematical Monthly, 109 (2), Mathematical Association of America: 105–120, doi:10.2307/2695324, JSTOR 2695324, MR 1903149. ?
- Thanks for the citation. Robson says: "Pythagorean triangles were a common subject for school mathematics problems in ancient Mesopotamia. This point has been made before (e.g. by Friberg)...." Here is what Friberg wrote: "Although Plimpton 322 is a unique text of its kind, there are several other known texts testifying that the Pythagorean Theorem was well-known to the mathematicians of the Old Babylonian period." I don't understand Robson as contradicting this statement by Friberg. Has anyone ever contradicted what Friberg said here in this quote?Anythingyouwant (talk) 14:59, 9 March 2015 (UTC)
- You mean like Robson, Eleanor (2002), "Words and pictures: new light on Plimpton 322" (PDF), American Mathematical Monthly, 109 (2), Mathematical Association of America: 105–120, doi:10.2307/2695324, JSTOR 2695324, MR 1903149. ?
- Please point to scholarly literature that says its disputed. We ought to cite it.Anythingyouwant (talk) 03:46, 9 March 2015 (UTC)
- If some reliable sources say one thing and some say others, we should not be choosing among them to pick what we want to say; we should be saying it is disputed. And if there is no undisputed predecessor of Pythagoras for this theorem, then clearly it is disputed. And your pointing to a popular-press oversimplification as a source when there is plenty of scholarly literature on this question is probably also not the best choice, at least by itself. —David Eppstein (talk) 02:36, 9 March 2015 (UTC)
- There are lots of sources that say the theorem was known earlier than Pythagorus (see, e.g. the Posamentier book linked in this Wikipedia article). Those reliable sources may well be wrong, as you suggest, but I am asking for a reliable source that says they are wrong. If no reliable source says so, then we are not supposed to write in the Wikipedia article that the matter is disputed. I am asking for a reliable source saying that it's disputed.Anythingyouwant (talk) 01:54, 9 March 2015 (UTC)
Knowledge of Pythagorean triangles and knowledge of the Pythagorean theorem are two completely different things. Please do not confuse one with the other. The 3-4-5 triangle is a Pythagorean triangle. Its existence in Egyptian mathematics, for instance, says nothing about whether the Egyptians knew about the relations of the areas of its squared edges. And as for who sources say was first to discover the theorem (not the integer right triangles but the theorem about the areas): Leon Lederman and Eli Maor both seem to be agreeing here that it was Pythagoras himself. Other sources, such as the one you used, disagree. So per WP:NPOV I think we have no alternative but to say that there is disagreement, rather than falsely implying that one side or the other is the scientific consensus. —David Eppstein (talk) 18:30, 9 March 2015 (UTC)
- Good work finding the Lederman statement. He's a physicist, and he apparently didn't mention anything about Babylon or Mesopotamia, but perhaps he is an adequate source for us to cite for the proposition that scholars disagree about who first discovered the Pythagorean Theorem.Anythingyouwant (talk) 20:01, 9 March 2015 (UTC)
Semi-protected edit request on 19 May 2015
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
Rather then referring to the catheti as "the other two sides" of the right triangle, why not refer them with their proper name? Besides, there is a nice Wikipedia article already which defines 'cathetus': http://en.wiki.x.io/wiki/Cathetus.
Thank you, Ivona
63.144.124.93 (talk) 22:21, 19 May 2015 (UTC)
 Partly done: I've wikilinked it to the Cathetus article. Stickee (talk) 22:42, 19 May 2015 (UTC)
Partly done: I've wikilinked it to the Cathetus article. Stickee (talk) 22:42, 19 May 2015 (UTC)
Hypotenuse
Note: this is about this revert: (DVdm (talk))
It's best to briefly explain the term and include a wikilink. That way they do not necessarily have to click on it to get an idea what it is.Anythingyouwant (talk) 16:13, 10 June 2015 (UTC)
- Agree and this is especially important in articles that deal with elementary topics where the probability is that the readers will not have the necessary prerequisite background. Forcing such readers to have to jump around to a dozen articles to get basic definitions is a very bad idea and likely to be a complete turn-off for them. Bill Cherowitzo (talk) 16:29, 10 June 2015 (UTC)
- I don't agree. Definition must be as short, clear and concise as possible. Are you going to explain what a function is in an article about derivative? Are you going to explain basic principles and terms of reaction engine in an article about rockets? This is not a kiddie book, this is Wikipedia, moreover, this is hypertext, the whole idea of which is hyperlink. Hyperlinking keywords and terms allows for short clear explanations, something that paper books cannot do. Mikus (talk) 06:13, 11 June 2015 (UTC)
- Yes, this is the Wikipedia and not a children's (or simple english) Wiki. However it safe to assume that many if not most adults have forgotten much of their middle school math, that is many of them may not understand hypotenuse but they will understand "side opposite of the right angle". Following hyperlinks should be a a fall back method/last resort to understand a given next, but not the default mode. A sign of good encyclopedic writing is usually to explain/illustrate without resorting to unnecessary technical jargon and/or introduce the required jargon in an understandable fashion on the side (if possible). In addition if an article has already an good or featured status, than imho in particular with regard to lead (but also already existing passages) conservative editing is advised. I.e. one should keep in mind that a lot of editors have already looked at the wording in the lead and considered it appropriate, so normally it shouldn't be changed on whim or based purely on personal preferences.--Kmhkmh (talk) 13:15, 20 July 2015 (UTC)
- See WP:TECHNICAL. Articles should be understandable to as wide an audience as possible. In this case, since the Pythagorean theorem is taught to school children, that is who, ideally, we should be aiming at, at least near the start of the article. Using polysyllabic jargon in the first sentence without defining it is counter to that goal. —David Eppstein (talk) 06:33, 11 June 2015 (UTC)
- I agree in the given context the version with explanation in brackets is the better one. The use of hyperlinks is not meant to outsource any short explanation or additional description one would use in a print article. If possible the most important part of an article should be understandable to audiences just by reading the article without chasing hyperlinks.--Kmhkmh (talk) 13:15, 20 July 2015 (UTC)
Per WP:LINKSTYLE, "Do not unnecessarily make a reader chase links: if a highly technical term can be simply explained with very few words, do so." It's customary to give a brief explanation of a highly technical term, plus a wikilink so the reader can find more info if the reader wants to.Anythingyouwant (talk) 18:56, 29 July 2015 (UTC)
- The policy is "Do not unnecessarily make a reader chase links: if a highly technical term can be simply explained with very few words, do so" from the very policy that you cite (WP:LINKSTYLE). WP:OVERLINK also requires a link to provide information necessary to understanding the article that is not already in the article. In this case 'hypotenuse' is explained in the immediately following parenthesized explanation that you insist on adding. If we take your insistence to its extreme, then 'square', 'right triangle', 'right angle' etc. etc. etc. should also have parenthesized short explanations.
- As far as your claim that "It's customary to give a brief explanation of a highly technical term, plus a wikilink so the reader can find more info if the reader wants to". Where is this documented as a policy? DieSwartzPunkt (talk) 14:15, 30 July 2015 (UTC)
- The very next sentence of WP:LINKSTYLE says that links may be okay even if they don't help to understand the sentence ("Do use a link wherever appropriate, but as far as possible do not force a reader to use that link to understand the sentence").Anythingyouwant (talk) 15:25, 30 July 2015 (UTC)
- My interpretation of that would be that your insistence at including the hyperlink is completely unnecessary because all the explanation that the reader requires to understand the subject is immediately after the word "hypotenuse". Unnecessary links should always be avoided where possible. 85.255.234.213 (talk) 16:33, 31 July 2015 (UTC)
- I disagree. The brief explanation is there in the article after the word and the link provides a more in-depth discussion of hypotenuses. Both are useful. —David Eppstein (talk) 17:36, 31 July 2015 (UTC)
- (edit conflict) @85.255.234.213: Sure, but the reader might not be merely interested in the explanation. Perhaps they also want to learn more about the linked subject, and they surely will find more than "all the explanation that the reader requires to understand." That is part of the philosophy of an encyclopedia. The link is certainly not unnecessary. It might even be necessary. - DVdm (talk) 17:43, 31 July 2015 (UTC)
- In that case the brief explanation is unnecessary, as the reader can click on the link and find the same information. The linked article tells you little beyond what is in this article anyway. Those users trying to defend the dual information are just trying to win an edit war using obfuscation and false arguments. 85.255.234.215 (talk) 22:44, 31 July 2015 (UTC)
- The link and the brief explanation serve two different purposes. The brief explanation is for people who just want to read this article without being confused by all the long words; the link is for people who know what hypotenuses are but want to find out more information about them. Why is it so difficult to understand that? —David Eppstein (talk) 22:56, 31 July 2015 (UTC)
- @85.255.234.215 please don't characterize fellow editor's motives. There is obviously more content in the article Hypotenuse than just the definition, content that a person reading this article might reasonably want to read, hence the hyperlink. It's as simple as that. Paul August ☎ 00:59, 1 August 2015 (UTC)
- In that case the brief explanation is unnecessary, as the reader can click on the link and find the same information. The linked article tells you little beyond what is in this article anyway. Those users trying to defend the dual information are just trying to win an edit war using obfuscation and false arguments. 85.255.234.215 (talk) 22:44, 31 July 2015 (UTC)
- My interpretation of that would be that your insistence at including the hyperlink is completely unnecessary because all the explanation that the reader requires to understand the subject is immediately after the word "hypotenuse". Unnecessary links should always be avoided where possible. 85.255.234.213 (talk) 16:33, 31 July 2015 (UTC)
- The very next sentence of WP:LINKSTYLE says that links may be okay even if they don't help to understand the sentence ("Do use a link wherever appropriate, but as far as possible do not force a reader to use that link to understand the sentence").Anythingyouwant (talk) 15:25, 30 July 2015 (UTC)
To be brutally frank, this is far too trivial a point to get overly worked up about. I do not propose to comment further. DieSwartzPunkt (talk) 12:35, 1 August 2015 (UTC)
- Our readers will be brutally grateful for that
 . - DVdm (talk) 10:06, 2 August 2015 (UTC)
. - DVdm (talk) 10:06, 2 August 2015 (UTC)
- Our editors too.--Kmhkmh (talk) 10:12, 2 August 2015 (UTC)
Semi-protected edit request on 22 October 2015
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
- ==See also==
- ==Notes==
Imeder (talk) 09:04, 22 October 2015 (UTC)
 Not done: Wikipedia does not take original research—see wp:NOR. Cheers - DVdm (talk) 09:41, 22 October 2015 (UTC)
Not done: Wikipedia does not take original research—see wp:NOR. Cheers - DVdm (talk) 09:41, 22 October 2015 (UTC)
- Also, per WP:SEEALSO, the links included in that section should only be to other Wikipedia articles. —David Eppstein (talk) 15:52, 22 October 2015 (UTC)
Better wording
Mesopotamian, Indian and Chinese mathematicians are all known to have discovered the theorem independently and, in some cases, provide proofs for special cases.
Shouldn't that be written as:
Mesopotamian, Indian and Chinese mathematicians are all known to have discovered the theorem independently and, in some cases, have provided proofs.
(Emphasis added) —User 000 name 18:09, 18 April 2015 (UTC)
- No. That implies incorrectly that these mathematicians proved the theorem in full generality. —David Eppstein (talk) 18:24, 18 April 2015 (UTC)
What about rewording the opening explanation, to include the phrase, "also known as the legs of the triangle" when mentioning the other two sides? — Preceding unsigned comment added by PA Math Prof (talk • contribs) 23:46, 7 November 2015 (UTC)
History section and Euclid
The treatment of the theorem in Euclid's Elements is not mentioned, though they are the oldest surviving original Greek source describing and possibly providing the first exact proof and some generalizations. Instead just Proclus' comment on Euclid is mentioned but with no information on the actual treatment in the Elements themselves.--Kmhkmh (talk) 07:35, 9 June 2015 (UTC)
The "In popular culture" mention of Neal Stephenson's use in Anathem would benefit from mentioning that the particular proof depicted there – only the diagram is given, with no explanation – is that of Euclid. Eddy, 84.215.30.244 (talk) 15:30, 19 July 2015 (UTC)
In the tail of the "Proof using similar triangles", the discussion claims "The underlying question is why Euclid did not use this proof, but invented another." I would have thought the reason for Euclid using the proof he did is that it directly shows the equality of areas, using shears and rotations. The theorem is about areas, so a proof in terms of areas is distinctly more satisfying than one in terms of ratios and products of lengths. Eddy 84.215.30.244 (talk) 11:55, 20 July 2015 (UTC)
The proof listed as Einstein's proof is Proposition 31 in Book VI of Euclid. In many schools children used to learn this proof before the age of 10. — Preceding unsigned comment added by 70.83.208.102 (talk) 02:49, 15 December 2015 (UTC)
explicit sources needed?
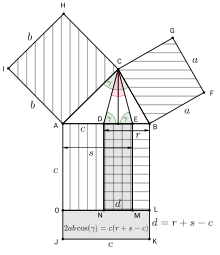
This edit is in dispute to an alleged lack of sources.
Do we really need a source explicitly stating the rather elementary connection between Ibn Qurra's generalization and the law of cosines? I'd rather file that under good writing and properly summarizing and contextualizing the existing sourced context. I mean you can probably find an explicit source somewhere, but since it so basic and just connects 2 sourced facts via 2 lines of middle school algebra, I don't think we need a source explicitly stating something like "Quarra's generalization is geometric version of the law of cosines". For the convenience of the discussion I added the disputed text in the subsection below--Kmhkmh (talk) 05:20, 16 December 2015 (UTC)
"unsourced" addition in dispute(?)
The theorem can also be seen as geometric version of the law of cosines from above:
This means the square over c needs to be extended or reduced by a rectangle of dimensions c and (r+s-c), so that its area matches the sum of the areas of squares over a and b. In other words the signed area of this rectangle is exactly the correction term of the law of cosines:
comments
Please sign all your talk page messages with four tildes (~~~~). Thanks.
Re "...just connects 2 sourced facts via 2 lines of middle school algebra..": that is precisely what wp:SYNTH is about. If this thing is sufficiently important to be mentioned here, then surely a textbook source must exist and should be easy to find, right? - DVdm (talk) 05:52, 16 December 2015 (UTC)
- We seem to have rather different reading of WP:SYNTH and proper encylopedic writing here, in any case I requested further feedback from the mathematics project.--Kmhkmh (talk) 05:59, 16 December 2015 (UTC)
- Twice ([3], [4]) I have replaced "... needs to extended or reduced with..." with "... needs to be extended or reduced with...". Do you think that "... needs to extended or reduced with..." is proper encylopedic writing and grammatically correct? - DVdm (talk) 06:09, 16 December 2015 (UTC)
- If you have an issue with the grammar or a missing word rather than the content in question, then that is separate discussion and you should clearly state so.--Kmhkmh (talk) 06:15, 16 December 2015 (UTC)
- Ok, I see that you re-inserted the "be". Thanks. - DVdm (talk) 07:01, 16 December 2015 (UTC)
- If you have an issue with the grammar or a missing word rather than the content in question, then that is separate discussion and you should clearly state so.--Kmhkmh (talk) 06:15, 16 December 2015 (UTC)
- Twice ([3], [4]) I have replaced "... needs to extended or reduced with..." with "... needs to be extended or reduced with...". Do you think that "... needs to extended or reduced with..." is proper encylopedic writing and grammatically correct? - DVdm (talk) 06:09, 16 December 2015 (UTC)
External links modified
Hello fellow Wikipedians,
I have just added archive links to one external link on Pythagorean theorem. Please take a moment to review my edit. If necessary, add {{cbignore}} after the link to keep me from modifying it. Alternatively, you can add {{nobots|deny=InternetArchiveBot}} to keep me off the page altogether. I made the following changes:
- Added archive https://web.archive.org/20071012135017/http://homepage.sefanet.ch:80/meylan-sa/saviez-vous1.htm to http://homepage.sefanet.ch/meylan-sa/saviez-vous1.htm
When you have finished reviewing my changes, please set the checked parameter below to true to let others know.
![]() An editor has reviewed this edit and fixed any errors that were found.
An editor has reviewed this edit and fixed any errors that were found.
- If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
- If you found an error with any archives or the URLs themselves, you can fix them with this tool.
Cheers.—cyberbot IITalk to my owner:Online 16:47, 30 January 2016 (UTC)
 Done: replaced dead url with archived one. - DVdm (talk) 20:09, 30 January 2016 (UTC)
Done: replaced dead url with archived one. - DVdm (talk) 20:09, 30 January 2016 (UTC)
Semi-protected edit request on 25 February 2016
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
Please add the following in the History section: According to Manjul Bhargava, here is a concrete source in India – namely, Baudhayana’s Sulba Sutra – that is before Pythagoras, and that has the Pythagorean theorem stated absolutely clearly. And, that goes back to around 800 BCE. The Pythagorean theorem is clearly stated there, with an interpretation in terms of areas that leads to a proof. [1] Ckundu (talk) 06:09, 25 February 2016 (UTC)
References
- Our article already mentions the Indian discovery but also states that the dates of the Sutra are given only within a wide range from 800-200BC and that the proof it contains is only for isosceles right triangles. Your request is to change that description to a maximalist interpretation in which what is in the Sutra is claimed for as early a date as possible, and without the isosceles qualification, on the basis of a jingoistic speech that completely ignores the other earlier precedents in Babylon and China? Why do you think that to be a properly neutral approach to the subject? —David Eppstein (talk) 06:26, 25 February 2016 (UTC)
External links modified
Hello fellow Wikipedians,
I have just modified one external link on Pythagorean theorem. Please take a moment to review my edit. If you have any questions, or need the bot to ignore the links, or the page altogether, please visit this simple FaQ for additional information. I made the following changes:
- Corrected formatting/usage for http://homepage.sefanet.ch:80/meylan-sa/saviez-vous1.htm
When you have finished reviewing my changes, please set the checked parameter below to true or failed to let others know (documentation at {{Sourcecheck}}).
![]() An editor has reviewed this edit and fixed any errors that were found.
An editor has reviewed this edit and fixed any errors that were found.
- If you have discovered URLs which were erroneously considered dead by the bot, you can report them with this tool.
- If you found an error with any archives or the URLs themselves, you can fix them with this tool.
Cheers.—cyberbot IITalk to my owner:Online 14:31, 2 April 2016 (UTC)
- I've checked this is working. CheCheDaWaff (talk) 08:34, 2 May 2016 (UTC)
Semi-protected edit request on 8 September 2016
This edit request to Pythagorean theorem has been answered. Set the |answered= or |ans= parameter to no to reactivate your request. |
In the subsection Pythagorean_theorem#Sets_of_m-dimensional_objects_in_n-dimensional_space, I think the mathematical statement of the Conant-Beyer theorem is excessively long, sometimes ambiguous and sometimes poorly worded. I therefore think that the part of this subsection from "in mathematical terms:" onwards should be replaced by the following text (which is largely taken from De_Gua's_theorem, so if these changes are made then De_Gua's_theorem should then be abbreviated, though I can do this myself):
More precisely, let U be a measurable subset of a k-dimensional affine subspace of (so ). For any subset with exactly k elements, let be the orthogonal projection of U onto the linear span of , where and is the standard basis for . Then
where is the k-dimensional volume of U and the sum is over all subsets with exactly k elements.
For example, suppose n = 3, k = 2 and U is the triangle in with vertices A, B and C lying on the -, - and -axes, respectively. The subsets of with exactly 2 elements are , and . By definition, is the orthogonal projection of onto the -plane, so is the triangle with vertices O, B and C, where O is the origin of . Similarly, and , so the Conant-Beyer theorem says
which is de Gua's theorem.
The Conant-Beyer theorem is essentially the inner-product-space version of the Pythagorean theorem applied to the kth exterior power of n-dimensional Euclidean space,[1] so it can be seen as both a generalization and a special case of the Pythagorean theorem.
References
- ^ Lemma 8 and Theorem 9 of James G. Dowty (2014). Volumes of logistic regression models with applications to model selection. arXiv:1408.0881v3 [math.ST ]
Jgdowty (talk) 02:47, 8 September 2016 (UTC)
 Not done - see wp:primary sources, wp:UNDUE, wp:PROMO, wp:NOR, wp:COI. - DVdm (talk) 08:52, 9 September 2016 (UTC)
Not done - see wp:primary sources, wp:UNDUE, wp:PROMO, wp:NOR, wp:COI. - DVdm (talk) 08:52, 9 September 2016 (UTC)
































