Talk:Gaussian surface
| This article is rated Start-class on Wikipedia's content assessment scale. It is of interest to the following WikiProjects: | |||||||||||
‹See TfM›
| |||||||||||
Cylindrical Gaussian surface
[edit]In the example calculation shouldn't it be rather than . Aren't we replacing the dot product with its definition? 186.42.32.13 (talk) 20:42, 13 February 2010 (UTC)
Spherical Surfaces
[edit]What is the reason that in a spherical, charges are present in the outersurface of the sphere? please answer me in email kalyan_kapil@yahoo.co.in waiting for reply please
- In the example given, the distribution of charge is a spherical shell, which means the charge is only present on the surface of the sphere Dom
Closed Surface Integrals
[edit]My math prof. told me that it's not an acceptable notation in math for an integral over closed surface. can anyone please post me a ref for the notation ? —Preceding unsigned comment added by 84.108.164.54 (talk) 23:02, 27 November 2007 (UTC)
clean up
[edit]I made various edits to clean up the article:
- Add links - too few
- {{oiint}} template
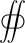 to the closed surface integrals
to the closed surface integrals - Nomenclature fixes
- Shorten cylinder derivation, make conscise, re-write to be written properly, looks very ropey,
- Extend explaination of spherical surface so clearer to the reader
- Add a few more referances:
- Remove ref in See also section attatched to Faraday cage (why there??) - it was the book from Griffiths so I used that in the lead
- Updated the Tipler and Mosca edition from 5th edn to 6th, used that for the derivations
-- F = q(E + v × B) 11:10, 25 February 2012 (UTC)
Definition
[edit]Simply defined as area in non-cartesian (Gaussian) coordinates. Isn't area more basic then flux? Amazing! Gaussian space is not constrained to three-dimensions either. AverageTurkishJoe (talk) 09:49, 20 November 2012 (UTC)
Infinite surfaces?
[edit]Is it possible to use an infinite plane as a Gaussian surface by setting the total charge in the extended euclidean space to zero by adding a charge to the point at infinity equal to negative the total charge in the whole space?
Example: Consider the field of a point charge of magnitude at the origin and an infinite plane parallel to the xy-plane but with a non-zero z coordinate , to balance the charge, another charge of magnitude is placed at infinity. Now the space is mapped to a Riemann hypersphere. This plane bisects the charge at the top while the bottom charge is fully on one side of the plane. Since the charge at infinity is bisected, the total charge on one side is and on the other side , thus the flux through the surface is (the sign depends on the orientation of the surface), this can be verified by taking the integral.
My claim is that, since the Riemann projection is conformal, any oriented infinite surface has a flux equal to where is the charge inside the surface, is the charge outside the surface and is the solid angle the interior of the surface occupies at the point at infinity (the limit of the area of the intersection of the interior of the surface and a sphere centred at any fixed point divided by the square of the radius as the sphere's radius tends to infinity).
For the example, assuming the charge is considered inside the surface, , and (in the limit, half the sphere is inside the surface) therefore, the formula yields; this is the result obtained previously and it makes sense because half the field lines intersect the plane.
My question is; does any of this make any sense?
74.109.213.249 (talk) 02:00, 8 February 2016 (UTC)
Definitions
[edit]In equations, epsilon0 shows up but is never defined. As a non-physicist, this is the third article I’ve clicked to in hopes of finding a definition, but no luck. Where would it be appropriate to define the vacuum permitivity variable (and link to the appropriate article)? 2600:1010:A020:81FE:A028:F6B3:A112:84C4 (talk) 16:39, 13 February 2024 (UTC)

















