Stochastic universal sampling
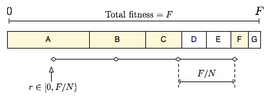
Stochastic universal sampling (SUS) is a selection technique used in evolutionary algorithms for selecting potentially useful solutions for recombination. It was introduced by James Baker.[1]
SUS is a development of fitness proportionate selection (FPS) which exhibits no bias and minimal spread. Where FPS chooses several solutions from the population by repeated random sampling, SUS uses a single random value to sample all of the solutions by choosing them at evenly spaced intervals. This gives weaker members of the population (according to their fitness) a chance to be chosen.
FPS can have bad performance when a member of the population has a really large fitness in comparison with other members. Using a comb-like ruler, SUS starts from a small random number, and chooses the next candidates from the rest of population remaining, not allowing the fittest members to saturate the candidate space.
Pseudo Code
[edit]Described as an algorithm, pseudocode for SUS looks like:
SUS(Population, N)
F := total fitness of Population
N := number of offspring to keep
P := distance between the pointers (F/N)
Start := random number between 0 and P
Pointers := [Start + i*P | i in [0..(N-1)]]
return RWS(Population,Pointers)
RWS(Population, Points)
Keep = []
for P in Points
I := 0
while fitness sum of Population[0..I] < P
I++
add Population[I] to Keep
return Keep
Where Population[0..I] is the set of individuals with array-index 0 to (and including) I.
Here RWS() describes the bulk of fitness proportionate selection (also known as "roulette wheel selection") – in true fitness proportional selection the parameter Points is always a (sorted) list of random numbers from 0 to F. The algorithm above is intended to be illustrative rather than canonical.
See also
[edit]References
[edit]- ^ Baker, James E. (1987). "Reducing Bias and Inefficiency in the Selection Algorithm". Proceedings of the Second International Conference on Genetic Algorithms and Their Application. Hillsdale, New Jersey: L. Erlbaum Associates: 14–21.
