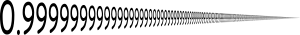Portal:Mathematics

The Mathematics Portal

Square root

Mathematics is the study of representing and reasoning about abstract objects (such as numbers, points, spaces, sets, structures, and games). Mathematics is used throughout the world as an essential tool in many fields, including natural science, engineering, medicine, and the social sciences. Applied mathematics, the branch of mathematics concerned with application of mathematical knowledge to other fields, inspires and makes use of new mathematical discoveries and sometimes leads to the development of entirely new mathematical disciplines, such as statistics and game theory. Mathematicians also engage in pure mathematics, or mathematics for its own sake, without having any application in mind. There is no clear line separating pure and applied mathematics, and practical applications for what began as pure mathematics are often discovered. (Full article...)

Featured articles –

  Featured articles are displayed here, which represent some of the best content on English Wikipedia.

---

• 
  
  

  

  Noether c. 1900–1910

  
  Amalie Emmy Noether (US: /ˈnʌtər/, UK: /ˈnɜːtə/; German: [ˈnøːtɐ]; 23 March 1882 – 14 April 1935) was a German mathematician who made many important contributions to abstract algebra. She proved Noether's first and second theorems, which are fundamental in mathematical physics. She was described by Pavel Alexandrov, Albert Einstein, Jean Dieudonné, Hermann Weyl and Norbert Wiener as the most important woman in the history of mathematics. As one of the leading mathematicians of her time, she developed theories of rings, fields, and algebras. In physics, Noether's theorem explains the connection between symmetry and conservation laws.
  
  Noether was born to a Jewish family in the Franconian town of Erlangen; her father was the mathematician Max Noether. She originally planned to teach French and English after passing the required examinations but instead studied mathematics at the University of Erlangen, where her father lectured. After completing her doctorate in 1907 under the supervision of Paul Gordan, she worked at the Mathematical Institute of Erlangen without pay for seven years. At the time, women were largely excluded from academic positions. In 1915, she was invited by David Hilbert and Felix Klein to join the mathematics department at the University of Göttingen, a world-renowned center of mathematical research. The philosophical faculty objected, however, and she spent four years lecturing under Hilbert's name. Her habilitation was approved in 1919, allowing her to obtain the rank of Privatdozent. (Full article...)
• 
  
  

  

  Archimedes Thoughtful
  by Domenico Fetti (1620)

  
  Archimedes of Syracuse (/ˌɑːrkɪˈmiːdiːz/ AR-kim-EE-deez; c. 287 – c. 212 BC) was an Ancient Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Considered the greatest mathematician of ancient history, and one of the greatest of all time, Archimedes anticipated modern calculus and analysis by applying the concept of the infinitely small and the method of exhaustion to derive and rigorously prove a range of geometrical theorems. These include the area of a circle, the surface area and volume of a sphere, the area of an ellipse, the area under a parabola, the volume of a segment of a paraboloid of revolution, the volume of a segment of a hyperboloid of revolution, and the area of a spiral.
  
  Archimedes' other mathematical achievements include deriving an approximation of pi, defining and investigating the Archimedean spiral, and devising a system using exponentiation for expressing very large numbers. He was also one of the first to apply mathematics to physical phenomena, working on statics and hydrostatics. Archimedes' achievements in this area include a proof of the law of the lever, the widespread use of the concept of center of gravity, and the enunciation of the law of buoyancy known as Archimedes' principle. He is also credited with designing innovative machines, such as his screw pump, compound pulleys, and defensive war machines to protect his native Syracuse from invasion. (Full article...)
• 
  
  

  

  Kaczynski after his arrest in 1996

  
  Theodore John Kaczynski (/kəˈzɪnski/ kə-ZIN-skee; May 22, 1942 – June 10, 2023), also known as the Unabomber (/ˈjuːnəbɒmər/ YOO-nə-bom-ər), was an American mathematician and domestic terrorist. He was a mathematics prodigy, but abandoned his academic career in 1969 to pursue a primitive lifestyle.
  
  Between 1978 and 1995, Kaczynski murdered three people and injured 23 others in a nationwide mail bombing campaign against people he believed to be advancing modern technology and the destruction of the natural environment. He authored Industrial Society and Its Future, a 35,000-word manifesto and social critique opposing all forms of technology, rejecting leftism, and advocating for a nature-centered form of anarchism. (Full article...)
• 

  

  The regular triangular tiling of the plane, whose symmetries are described by the affine symmetric group S̃₃

  
  The affine symmetric groups are a family of mathematical structures that describe the symmetries of the number line and the regular triangular tiling of the plane, as well as related higher-dimensional objects. In addition to this geometric description, the affine symmetric groups may be defined in other ways: as collections of permutations (rearrangements) of the integers (..., −2, −1, 0, 1, 2, ...) that are periodic in a certain sense, or in purely algebraic terms as a group with certain generators and relations. They are studied in combinatorics and representation theory.
  
  A finite symmetric group consists of all permutations of a finite set. Each affine symmetric group is an infinite extension of a finite symmetric group. Many important combinatorial properties of the finite symmetric groups can be extended to the corresponding affine symmetric groups. Permutation statistics such as descents and inversions can be defined in the affine case. As in the finite case, the natural combinatorial definitions for these statistics also have a geometric interpretation. (Full article...)
• 

  

  The manipulations of the Rubik's Cube form the Rubik's Cube group.

  
  In mathematics, a group is a set with an operation that satisfies the following constraints: the operation is associative and has an identity element, and every element of the set has an inverse element. The set is closed under the operation.
  
  Many mathematical structures are groups endowed with other properties. For example, the integers with the addition operation form an infinite group, which is generated by a single element called ⁠$1$⁠ (these properties characterize the integers in a unique way). (Full article...)
• 

  

  The first 15,000 partial sums of 0 + 1 − 2 + 3 − 4 + ... The graph is situated with positive integers to the right and negative integers to the left.

  
  
  In mathematics, 1 − 2 + 3 − 4 + ··· is an infinite series whose terms are the successive positive integers, given alternating signs. Using sigma summation notation the sum of the first m terms of the series can be expressed as
  $$\sum _{n=1}^{m}n(-1)^{n-1}.$$
  
  The infinite series diverges, meaning that its sequence of partial sums, (1, −1, 2, −2, 3, ...), does not tend towards any finite limit. Nonetheless, in the mid-18th century, Leonhard Euler wrote what he admitted to be a paradoxical equation:
  $$1-2+3-4+\cdots ={\frac {1}{4}}.$$ (Full article...)
• 
  
  

  

  Bust of Shen at the Beijing Ancient Observatory

  
  Shen Kuo (Chinese: 沈括; 1031–1095) or Shen Gua, courtesy name Cunzhong (存中) and pseudonym Mengqi (now usually given as Mengxi) Weng (夢溪翁), was a Chinese polymath, scientist, and statesman of the Song dynasty (960–1279). Shen was a master in many fields of study including mathematics, optics, and horology. In his career as a civil servant, he became a finance minister, governmental state inspector, head official for the Bureau of Astronomy in the Song court, Assistant Minister of Imperial Hospitality, and also served as an academic chancellor. At court his political allegiance was to the Reformist faction known as the New Policies Group, headed by Chancellor Wang Anshi (1021–1085).
  
  In his Dream Pool Essays or Dream Torrent Essays (夢溪筆談; Mengxi Bitan) of 1088, Shen was the first to describe the magnetic needle compass, which would be used for navigation (first described in Europe by Alexander Neckam in 1187). Shen discovered the concept of true north in terms of magnetic declination towards the north pole, with experimentation of suspended magnetic needles and "the improved meridian determined by Shen's [astronomical] measurement of the distance between the pole star and true north". This was the decisive step in human history to make compasses more useful for navigation, and may have been a concept unknown in Europe for another four hundred years (evidence of German sundials made circa 1450 show markings similar to Chinese geomancers' compasses in regard to declination). (Full article...)
• 
  In algebraic geometry and theoretical physics, mirror symmetry is a relationship between geometric objects called Calabi–Yau manifolds. The term refers to a situation where two Calabi–Yau manifolds look very different geometrically but are nevertheless equivalent when employed as extra dimensions of string theory.
  
  Early cases of mirror symmetry were discovered by physicists. Mathematicians became interested in this relationship around 1990 when Philip Candelas, Xenia de la Ossa, Paul Green, and Linda Parkes showed that it could be used as a tool in enumerative geometry, a branch of mathematics concerned with counting the number of solutions to geometric questions. Candelas and his collaborators showed that mirror symmetry could be used to count rational curves on a Calabi–Yau manifold, thus solving a longstanding problem. Although the original approach to mirror symmetry was based on physical ideas that were not understood in a mathematically precise way, some of its mathematical predictions have since been proven rigorously. (Full article...)
• 

  

  Stylistic impression of the number, representing how its decimals go on infinitely

  
  In mathematics, 0.999... (also written as 0.9, 0..9 or 0.(9)) denotes the smallest number greater than every number in the sequence (0.9, 0.99, 0.999, ...). It can be proved that this number is 1; that is,
  : $0.999...=1.$
  In other words, 0.999... is not "almost exactly 1" or "very, very nearly but not quite 1"; rather, 0.999... and "1" are exactly the same number.
  
  An elementary proof is given below that involves only elementary arithmetic and the fact that there is no positive real number less than all 1/10ⁿ, where n is a natural number, a property that results immediately from the Archimedean property of the real numbers. (Full article...)
• 
  
  

  

  Cantor, c. 1910

  
  Georg Ferdinand Ludwig Philipp Cantor (/ˈkæntɔːr/ KAN-tor, German: [ˈɡeːɔʁk ˈfɛʁdinant ˈluːtvɪç ˈfiːlɪp ˈkantoːɐ̯]; 3 March [O.S. 19 February] 1845 – 6 January 1918) was a mathematician who played a pivotal role in the creation of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets, and proved that the real numbers are more numerous than the natural numbers. Cantor's method of proof of this theorem implies the existence of an infinity of infinities. He defined the cardinal and ordinal numbers and their arithmetic. Cantor's work is of great philosophical interest, a fact he was well aware of.
  
  Originally, Cantor's theory of transfinite numbers was regarded as counter-intuitive – even shocking. This caused it to encounter resistance from mathematical contemporaries such as Leopold Kronecker and Henri Poincaré and later from Hermann Weyl and L. E. J. Brouwer, while Ludwig Wittgenstein raised philosophical objections; see Controversy over Cantor's theory. Cantor, a devout Lutheran Christian, believed the theory had been communicated to him by God. Some Christian theologians (particularly neo-Scholastics) saw Cantor's work as a challenge to the uniqueness of the absolute infinity in the nature of God – on one occasion equating the theory of transfinite numbers with pantheism – a proposition that Cantor vigorously rejected. Not all theologians were against Cantor's theory; prominent neo-scholastic philosopher Constantin Gutberlet was in favor of it and Cardinal Johann Baptist Franzelin accepted it as a valid theory (after Cantor made some important clarifications). (Full article...)
• 

  

  Figure 1: A solution (in purple) to Apollonius's problem. The given circles are shown in black.

  
  
  In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 BC – c. 190 BC) posed and solved this famous problem in his work Ἐπαφαί (Epaphaí, "Tangencies"); this work has been lost, but a 4th-century AD report of his results by Pappus of Alexandria has survived. Three given circles generically have eight different circles that are tangent to them (Figure 2), a pair of solutions for each way to divide the three given circles in two subsets (there are 4 ways to divide a set of cardinality 3 in 2 parts).
  
  In the 16th century, Adriaan van Roomen solved the problem using intersecting hyperbolas, but this solution does not use only straightedge and compass constructions. François Viète found such a solution by exploiting limiting cases: any of the three given circles can be shrunk to zero radius (a point) or expanded to infinite radius (a line). Viète's approach, which uses simpler limiting cases to solve more complicated ones, is considered a plausible reconstruction of Apollonius' method. The method of van Roomen was simplified by Isaac Newton, who showed that Apollonius' problem is equivalent to finding a position from the differences of its distances to three known points. This has applications in navigation and positioning systems such as LORAN. (Full article...)
• 

  

  
  Josiah Willard Gibbs (/ɡɪbz/; February 11, 1839 – April 28, 1903) was an American scientist who made significant theoretical contributions to physics, chemistry, and mathematics. His work on the applications of thermodynamics was instrumental in transforming physical chemistry into a rigorous deductive science. Together with James Clerk Maxwell and Ludwig Boltzmann, he created statistical mechanics (a term that he coined), explaining the laws of thermodynamics as consequences of the statistical properties of ensembles of the possible states of a physical system composed of many particles. Gibbs also worked on the application of Maxwell's equations to problems in physical optics. As a mathematician, he created modern vector calculus (independently of the British scientist Oliver Heaviside, who carried out similar work during the same period) and described the Gibbs phenomenon in the theory of Fourier analysis.
  
  In 1863, Yale University awarded Gibbs the first American doctorate in engineering. After a three-year sojourn in Europe, Gibbs spent the rest of his career at Yale, where he was a professor of mathematical physics from 1871 until his death in 1903. Working in relative isolation, he became the earliest theoretical scientist in the United States to earn an international reputation and was praised by Albert Einstein as "the greatest mind in American history." In 1901, Gibbs received what was then considered the highest honor awarded by the international scientific community, the Copley Medal of the Royal Society of London, "for his contributions to mathematical physics." (Full article...)
• 

  

  High-precision test of general relativity by the Cassini space probe (artist's impression): radio signals sent between the Earth and the probe (green wave) are delayed by the warping of spacetime (blue lines) due to the Sun's mass.

  
  
  General relativity is a theory of gravitation developed by Albert Einstein between 1907 and 1915. The theory of general relativity says that the observed gravitational effect between masses results from their warping of spacetime.
  
  By the beginning of the 20th century, Newton's law of universal gravitation had been accepted for more than two hundred years as a valid description of the gravitational force between masses. In Newton's model, gravity is the result of an attractive force between massive objects. Although even Newton was troubled by the unknown nature of that force, the basic framework was extremely successful at describing motion. (Full article...)
• 
  
  

  

  Title page of the first edition of Wright's Certaine Errors in Navigation (1599)

  
  Edward Wright (baptised 8 October 1561; died November 1615) was an English mathematician and cartographer noted for his book Certaine Errors in Navigation (1599; 2nd ed., 1610), which for the first time explained the mathematical basis of the Mercator projection by building on the works of Pedro Nunes, and set out a reference table giving the linear scale multiplication factor as a function of latitude, calculated for each minute of arc up to a latitude of 75°. This was in fact a table of values of the integral of the secant function, and was the essential step needed to make practical both the making and the navigational use of Mercator charts.
  
  Wright was born at Garveston in Norfolk and educated at Gonville and Caius College, Cambridge, where he became a fellow from 1587 to 1596. In 1589 the college granted him leave after Elizabeth I requested that he carry out navigational studies with a raiding expedition organised by the Earl of Cumberland to the Azores to capture Spanish galleons. The expedition's route was the subject of the first map to be prepared according to Wright's projection, which was published in Certaine Errors in 1599. The same year, Wright created and published the first world map produced in England and the first to use the Mercator projection since Gerardus Mercator's original 1569 map. (Full article...)
• 

  

  
  Richard Phillips Feynman (/ˈfaɪnmən/; May 11, 1918 – February 15, 1988) was an American theoretical physicist, known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics, the physics of the superfluidity of supercooled liquid helium, as well as his work in particle physics for which he proposed the parton model. For his contributions to the development of quantum electrodynamics, Feynman received the Nobel Prize in Physics in 1965 jointly with Julian Schwinger and Shin'ichirō Tomonaga.
  
  Feynman developed a widely used pictorial representation scheme for the mathematical expressions describing the behavior of subatomic particles, which later became known as Feynman diagrams. During his lifetime, Feynman became one of the best-known scientists in the world. In a 1999 poll of 130 leading physicists worldwide by the British journal Physics World, he was ranked the seventh-greatest physicist of all time. (Full article...)

Selected image –

three lines connecting corresponding vertices of a larger triangle on the left and a smaller one on the right converge at a point further to the right called the "center of perspectivity"

Desargues's theorem

Credit: User:Jujutacular, based on an original by User:DynaBlast

In projective geometry, Desargues' theorem states that two triangles are in perspective axially if and only if they are in perspective centrally. Lines through the triangle sides meet in pairs at collinear points along the axis of perspectivity. Lines through corresponding pairs of vertices on the triangles meet at a point called the center of perspectivity.

Good articles –

  These are Good articles, which meet a core set of high editorial standards.

---

• 
  
  

  

  Photograph of Maxwell in his 40s

  
  James Clerk Maxwell FRS FRSE (13 June 1831 – 5 November 1879) was a Scottish physicist with broad interests who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism and light as different manifestations of the same phenomenon. Maxwell's equations for electromagnetism have been called the "second great unification in physics" where the first one had been realised by Isaac Newton.
  
  With the publication of "A Dynamical Theory of the Electromagnetic Field" in 1865, Maxwell demonstrated that electric and magnetic fields travel through space as waves moving at the speed of light. He proposed that light is an undulation in the same medium that is the cause of electric and magnetic phenomena. The unification of light and electrical phenomena led to his prediction of the existence of radio waves. Maxwell is also regarded as a founder of the modern field of electrical engineering. (Full article...)
• 

  

  Geometric representation of the square pyramidal number 1 + 4 + 9 + 16 = 30.

  
  In mathematics, a pyramid number, or square pyramidal number, is a natural number that counts the stacked spheres in a pyramid with a square base. The study of these numbers goes back to Archimedes and Fibonacci. They are part of a broader topic of figurate numbers representing the numbers of points forming regular patterns within different shapes.
  
  As well as counting spheres in a pyramid, these numbers can be described algebraically as a sum of the first $n$ positive square numbers, or as the values of a cubic polynomial. They can be used to solve several other counting problems, including counting squares in a square grid and counting acute triangles formed from the vertices of an odd regular polygon. They equal the sums of consecutive tetrahedral numbers, and are one-fourth of a larger tetrahedral number. The sum of two consecutive square pyramidal numbers is an octahedral number. (Full article...)
• 
  
  

  

  Ross in 1970

  
  Arnold Ephraim Ross (August 24, 1906 – September 25, 2002) was a mathematician and educator who founded the Ross Mathematics Program, a number theory summer program for gifted high school students. He was born in Chicago, but spent his youth in Odesa, Ukraine, where he studied with Samuil Shatunovsky. Ross returned to Chicago and enrolled in University of Chicago graduate coursework under E. H. Moore, despite his lack of formal academic training. He received his Ph.D. and married his wife, Bee, in 1931.
  
  Ross taught at several institutions including St. Louis University before becoming chair of University of Notre Dame's mathematics department in 1946. He started a teacher training program in mathematics that evolved into the Ross Mathematics Program in 1957 with the addition of high school students. The program moved with him to Ohio State University when he became their department chair in 1963. Though forced to retire in 1976, Ross ran the summer program until 2000. He had worked with over 2,000 students during more than forty summers. (Full article...)
• 
  
  

  

  L6a4

  
  In mathematics, the Borromean rings are three simple closed curves in three-dimensional space that are topologically linked and cannot be separated from each other, but that break apart into two unknotted and unlinked loops when any one of the three is cut or removed. Most commonly, these rings are drawn as three circles in the plane, in the pattern of a Venn diagram, alternatingly crossing over and under each other at the points where they cross. Other triples of curves are said to form the Borromean rings as long as they are topologically equivalent to the curves depicted in this drawing.
  
  The Borromean rings are named after the Italian House of Borromeo, who used the circular form of these rings as an element of their coat of arms, but designs based on the Borromean rings have been used in many cultures, including by the Norsemen and in Japan. They have been used in Christian symbolism as a sign of the Trinity, and in modern commerce as the logo of Ballantine beer, giving them the alternative name Ballantine rings. Physical instances of the Borromean rings have been made from linked DNA or other molecules, and they have analogues in the Efimov state and Borromean nuclei, both of which have three components bound to each other although no two of them are bound. (Full article...)
• 
  Fermat's Last Tango is a 2000 off-Broadway musical about the proof of Fermat's Last Theorem, written by husband and wife Joshua Rosenblum (music, lyrics) and Joanne Sydney Lessner (book, lyrics). The musical presents a fictionalized version of the real life story of Andrew Wiles, and has been praised for the accuracy of the mathematical content. The original production at the York Theatre received mixed reviews, but the musical was well received by mathematical audiences. A video of the original production has been distributed by the Clay Mathematics Institute and shown at several mathematical conferences and similar occasions. The musical has also been translated into Portuguese. (Full article...)
• 

  

  Georg Cantor,     c. 1870

  
  Cantor's first set theory article contains Georg Cantor's first theorems of transfinite set theory, which studies infinite sets and their properties. One of these theorems is his "revolutionary discovery" that the set of all real numbers is uncountably, rather than countably, infinite. This theorem is proved using Cantor's first uncountability proof, which differs from the more familiar proof using his diagonal argument. The title of the article, "On a Property of the Collection of All Real Algebraic Numbers" ("Ueber eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen"), refers to its first theorem: the set of real algebraic numbers is countable. Cantor's article was published in 1874. In 1879, he modified his uncountability proof by using the topological notion of a set being dense in an interval.
  
  Cantor's article also contains a proof of the existence of transcendental numbers. Both constructive and non-constructive proofs have been presented as "Cantor's proof." The popularity of presenting a non-constructive proof has led to a misconception that Cantor's arguments are non-constructive. Since the proof that Cantor published either constructs transcendental numbers or does not, an analysis of his article can determine whether or not this proof is constructive. Cantor's correspondence with Richard Dedekind shows the development of his ideas and reveals that he had a choice between two proofs: a non-constructive proof that uses the uncountability of the real numbers and a constructive proof that does not use uncountability. (Full article...)
• 
  In mathematics, economics, and computer science, the Gale–Shapley algorithm (also known as the deferred acceptance algorithm, propose-and-reject algorithm, or Boston Pool algorithm) is an algorithm for finding a solution to the stable matching problem. It is named for David Gale and Lloyd Shapley, who published it in 1962, although it had been used for the National Resident Matching Program since the early 1950s. Shapley and Alvin E. Roth (who pointed out its prior application) won the 2012 Nobel Prize in Economics for work including this algorithm.
  
  The stable matching problem seeks to pair up equal numbers of participants of two types, using preferences from each participant. The pairing must be stable: no pair of participants should prefer each other to their assigned match. In each round of the Gale–Shapley algorithm, unmatched participants of one type propose a match to the next participant on their preference list. Each proposal is accepted if its recipient prefers it to their current match. The resulting procedure is a truthful mechanism from the point of view of the proposing participants, who receive their most-preferred pairing consistent with stability. In contrast, the recipients of proposals receive their least-preferred pairing. The algorithm can be implemented to run in time quadratic in the number of participants, and linear in the size of the input to the algorithm. (Full article...)
• 
  In control system theory, and various branches of engineering, a transfer function matrix, or just transfer matrix is a generalisation of the transfer functions of single-input single-output (SISO) systems to multiple-input and multiple-output (MIMO) systems. The matrix relates the outputs of the system to its inputs. It is a particularly useful construction for linear time-invariant (LTI) systems because it can be expressed in terms of the s-plane.
  
  In some systems, especially ones consisting entirely of passive components, it can be ambiguous which variables are inputs and which are outputs. In electrical engineering, a common scheme is to gather all the voltage variables on one side and all the current variables on the other regardless of which are inputs or outputs. This results in all the elements of the transfer matrix being in units of impedance. The concept of impedance (and hence impedance matrices) has been borrowed into other energy domains by analogy, especially mechanics and acoustics. (Full article...)
• 

  

  A unit distance graph with 16 vertices and 40 edges

  
  In mathematics, particularly geometric graph theory, a unit distance graph is a graph formed from a collection of points in the Euclidean plane by connecting two points whenever the distance between them is exactly one. To distinguish these graphs from a broader definition that allows some non-adjacent pairs of vertices to be at distance one, they may also be called strict unit distance graphs or faithful unit distance graphs. As a hereditary family of graphs, they can be characterized by forbidden induced subgraphs. The unit distance graphs include the cactus graphs, the matchstick graphs and penny graphs, and the hypercube graphs. The generalized Petersen graphs are non-strict unit distance graphs.
  
  An unsolved problem of Paul Erdős asks how many edges a unit distance graph on $n$ vertices can have. The best known lower bound is slightly above linear in $n$—far from the upper bound, proportional to $n^{4/3}$. The number of colors required to color unit distance graphs is also unknown (the Hadwiger–Nelson problem): some unit distance graphs require five colors, and every unit distance graph can be colored with seven colors. For every algebraic number there is a unit distance graph with two vertices that must be that distance apart. According to the Beckman–Quarles theorem, the only plane transformations that preserve all unit distance graphs are the isometries. (Full article...)
• 

  

  The integer number line, a set of infinitely many points with integer distances. According to the Erdős–Anning theorem, any such set lies on a line.

  
  The Erdős–Anning theorem states that, whenever an infinite number of points in the plane all have integer distances, the points lie on a straight line. The same result holds in higher dimensional Euclidean spaces.
  The theorem cannot be strengthened to give a finite bound on the number of points: there exist arbitrarily large finite sets of points that are not on a line and have integer distances.
  
  The theorem is named after Paul Erdős and Norman H. Anning, who published a proof of it in 1945. Erdős later supplied a simpler proof, which can also be used to check whether a point set forms an Erdős–Diophantine graph, an inextensible system of integer points with integer distances. The Erdős–Anning theorem inspired the Erdős–Ulam problem on the existence of dense point sets with rational distances. (Full article...)
• 

  

  The graph of the 3-3 duoprism (the line graph of $K_{3,3}$) is perfect. Here it is colored with three colors, with one of its 3-vertex maximum cliques highlighted.

  
  In graph theory, a perfect graph is a graph in which the chromatic number equals the size of the maximum clique, both in the graph itself and in every induced subgraph. In all graphs, the chromatic number is greater than or equal to the size of the maximum clique, but they can be far apart. A graph is perfect when these numbers are equal, and remain equal after the deletion of arbitrary subsets of vertices.
  
  The perfect graphs include many important families of graphs and serve to unify results relating colorings and cliques in those families. For instance, in all perfect graphs, the graph coloring problem, maximum clique problem, and maximum independent set problem can all be solved in polynomial time, despite their greater complexity for non-perfect graphs. In addition, several important minimax theorems in combinatorics, including Dilworth's theorem and Mirsky's theorem on partially ordered sets, Kőnig's theorem on matchings, and the Erdős–Szekeres theorem on monotonic sequences, can be expressed in terms of the perfection of certain associated graphs. (Full article...)
• 
  
  

  

  Wigner in 1963

  
  Eugene Paul Wigner (Hungarian: Wigner Jenő Pál, pronounced [ˈviɡnɛr ˈjɛnøː ˈpaːl]; November 17, 1902 – January 1, 1995) was a Hungarian-American theoretical physicist who also contributed to mathematical physics. He received the Nobel Prize in Physics in 1963 "for his contributions to the theory of the atomic nucleus and the elementary particles, particularly through the discovery and application of fundamental symmetry principles".
  
  A graduate of the Technical University of Berlin, Wigner worked as an assistant to Karl Weissenberg and Richard Becker at the Kaiser Wilhelm Institute in Berlin, and David Hilbert at the University of Göttingen. Wigner and Hermann Weyl were responsible for introducing group theory into physics, particularly the theory of symmetry in physics. Along the way he performed ground-breaking work in pure mathematics, in which he authored a number of mathematical theorems. In particular, Wigner's theorem is a cornerstone in the mathematical formulation of quantum mechanics. He is also known for his research into the structure of the atomic nucleus. In 1930, Princeton University recruited Wigner, along with John von Neumann, and he moved to the United States, where he obtained citizenship in 1937. (Full article...)

Did you know (auto-generated) –

• ... that a folded paper lantern shows that certain mathematical definitions of surface area are incorrect?
• ... that Arithmetic was the first mathematics text book written in the Russian language?
• ... that ten-sided gaming dice have kite-shaped faces?
• ... that in the aftermath of the American Civil War, the only Black-led organization providing teachers to formerly enslaved people was the African Civilization Society?
• ... that museum director Alena Aladava rebuilt the Belarusian national art collection in the aftermath of the Second World War?
• ... that Latvian-Soviet artist Karlis Johansons exhibited a skeletal tensegrity form of the Schönhardt polyhedron seven years before Erich Schönhardt's 1928 paper on its mathematics?
• ... that subgroup distortion theory, introduced by Misha Gromov in 1993, can help encode text?
• ... that Fairleigh Dickinson's upset victory over Purdue was the biggest upset in terms of point spread in NCAA tournament history, with Purdue being a 23+1⁄2-point favorite?

More did you know –

Did you know...

• ...that the sum of the first n odd numbers divided by the sum of the next n odd numbers is always equal to one third?
• ...that i to the power of i, where i is the square root of -1, is a real number?
• ...an infinite, nonrepeating decimal can be represented using only the number 1 using continued fractions?
• ...that 253931039382791 and the following 18 prime numbers all end in the digit 1?
• ...that the Electronic Frontier Foundation funds awards for the discovery of prime numbers beyond certain sizes?
• ...that pi can be computed using only the number 2 by the work of Viète?
• … that the Riemann Hypothesis, one of the Millennium Problems, depends on the asymptotic growth of the Mertens Function?

Selected article –

Banach–Tarski paradox Image credit: Benjamin D. Esham

The Banach–Tarski paradox is a theorem in set-theoretic geometry which states that a solid ball in 3-dimensional space can be split into a finite number of non-overlapping pieces, which can then be put back together in a different way to yield two identical copies of the original ball. The reassembly process involves only moving the pieces around and rotating them, without changing their shape. However, the pieces themselves are complicated: they are not usual solids but infinite scatterings of points. A stronger form of the theorem implies that given any two "reasonable" solid objects (such as a small ball and a huge ball) — solid in the sense of the continuum — either one can be reassembled into the other. This is often stated colloquially as "a pea can be chopped up and reassembled into the Sun". (Full article...)

View all selected articles

Subcategories

Algebra | Arithmetic | Analysis | Complex analysis | Applied mathematics | Calculus | Category theory | Chaos theory | Combinatorics | Dynamical systems | Fractals | Game theory | Geometry | Algebraic geometry | Graph theory | Group theory | Linear algebra | Mathematical logic | Model theory | Multi-dimensional geometry | Number theory | Numerical analysis | Optimization | Order theory | Probability and statistics | Set theory | Statistics | Topology | Algebraic topology | Trigonometry | Linear programming

---

Mathematics | History of mathematics | Mathematicians | Awards | Education | Literature | Notation | Organizations | Theorems | Proofs | Unsolved problems

Full category tree. Select [►] to view subcategories.

Mathematics

Mathematics by country

Fields of mathematics

Mathematics-related lists

Mathematicians

Works about mathematics

Mathematics and art

Mathematical classification systems

Mathematical concepts

Mathematical constants

Mathematics and culture

Eponyms in mathematics

Mathematical examples

History of mathematics

Mathematical notation

Mathematical science occupations

Outlines of mathematics and logic

Philosophy of mathematics

Mathematical projects

Mathematical proofs

Pseudomathematics

Set index articles on mathematics

Mathematical terminology

Mathematical theorems

Mathematical tools

Mathematics stubs

Topics in mathematics

General	Foundations	Number theory	Discrete mathematics
Mathematicians History of mathematics Philosophy of mathematics Mathematical notation Mathematical beauty Mathematics education Glossary of mathematical symbols	Foundations of mathematics Mathematical logic Proof theory Gödel's incompleteness theorems Model theory Recursion theory Set theory Naive set theory Axiomatic set theory Category theory Topos theory	Number theory Algebraic number theory Analytic number theory Arithmetic Fundamental theorem of arithmetic Numbers Natural numbers Prime numbers Rational numbers Algebraic numbers	Discrete mathematics Combinatorics Combinatorial geometry Coding theory Combinatorial design Enumerative combinatorics Combinatorial optimization Graph theory Order theory Lattice theory Digital Signal Processing Theoretical computer science Computability theory Complexity theory
Algebra	Analysis	Geometry and topology	Applied mathematics
Algebra Elementary algebra Abstract algebra Group theory Ring theory Field theory Commutative algebra Geometric algebra Linear algebra Matrix theory Multilinear algebra Universal algebra Fundamental theorem of algebra	Analysis Calculus Fundamental theorem of calculus Vector calculus Geometric calculus Measure theory Real analysis Complex analysis Differential equations Ordinary differential equations Partial differential equations Integral equations Approximation theory Special functions Potential theory Harmonic analysis Fourier analysis Functional analysis Operator theory	Geometry Euclidean geometry Trigonometry Analytic geometry Non-Euclidean geometry Affine geometry Projective geometry Convex geometry Discrete geometry Algebraic geometry Differential geometry K theory Gauge theory Riemannian geometry Lie groups Topology General topology Algebraic topology Geometric topology Differential topology	Applied mathematics Mathematical modeling Mathematical physics Dynamical systems Control theory Calculus of variations Optimization Mathematical economics Game theory Mathematical finance Statistics Probability theory Stochastic processes Numerical analysis Cryptography Information theory

Index of mathematics articles

ARTICLE INDEX:	0–9 A B C D E F G H I J K L M N O P Q R S T U V W X Y Z
MATHEMATICIANS:	A B C D E F G H I J K L M N O P Q R S T U V W X Y Z

Related portals

WikiProjects

The Mathematics WikiProject is the center for mathematics-related editing on Wikipedia. Join the discussion on the project's talk page.

Project pages

• Participants
• Current activity
• Manual of style
• Conventions

Essays

• Advice on using Wikipedia for mathematics self-study
• Proofs

Subprojects

• PlanetMath Exchange (Talk)
• Graphics (Talk)
• Article assessment (Talk)

Related projects

Computer science | Cryptography | Game theory | Numbers | Physics | Science | Statistics

Things you can do

• Create a new article: List of requested articles
• Add a new image: Image requests
• Expand an article: Mathematics stubs
• Lend your expertise: Expert attention needed

In other Wikimedia projects

The following Wikimedia Foundation sister projects provide more on this subject:

• 

  Commons
  Free media repository

• 

  Wikibooks
  Free textbooks and manuals

• 

  Wikidata
  Free knowledge base

• 

  Wikinews
  Free-content news

• 

  Wikiquote
  Collection of quotations

• 

  Wikisource
  Free-content library

• 

  Wikiversity
  Free learning tools

• 

  Wiktionary
  Dictionary and thesaurus

More portals

Discover Wikipedia using portals

• 

  List of all portals

• 

  The arts portal

• 

  Biography portal

• 

  Current events portal

• 

  Geography portal

• 

  History portal

• 

  Mathematics portal

• 

  Science portal

• 

  Society portal

• 

  Technology portal

• 

  Random portal

• 

  WikiProject Portals