Maximal unique match
This article needs additional citations for verification. (May 2021) |
A maximal unique match or MUM, for short, is part of a key step [1] in the multiple sequence alignment of genomes in computational biology. Identification of MUMs and other potential anchors is the first step in larger alignment systems such as MUMmer. Anchors are the areas between two genomes where they are highly similar. To understand what a MUM is we each word in the acronym can be broken down individually. Match implies that the substring occurs in both sequences to be aligned. Unique means that the substring occurs only once in each sequence. Finally, maximal states that the substring is not part of another larger string that fulfills both prior requirements. The idea behind this is that long sequences that match exactly and occur only once in each genome are almost certainly part of the global alignment.
Formal definition
[edit]"Given two genomes A and B, Maximal Unique Match (MUM) substring is a common substring of A and B of length longer than a specified minimum length d (by default d = 20) such that
- it is maximal, that is, it cannot be extended on either end without incurring a mismatch and
- it is unique in both sequences"[2]
Algorithm
[edit]Identifying the set of MUMs in two very long genome sequences is not computationally trivial.[1] There are several algorithmic ways to approach identifying MUMs in multiple sequence alignment. The simplest and slowest method is using brute force where for every index i in genome A and every index j in genome B , you calculate the longest common prefix (P) of A[i...n] and B[j...m]. Next you must guarantee that the length of P is at least d where d is the minimum MUM size specified. Finally you must ensure that P is unique in both genomes. The complexity of the brute force method is thus O(mn).[2]
In actuality though MUMs are identified by building a generalized suffix tree for A and B . A list is then created for all internal nodes with exactly one child from each genome sequence. For each of these nodes(we will identify children from genome A as i and children from genome B as j ) check that A[i-1] ≠ B[j-1] and for those where this conditions holds, we know this is a MUM. In this case the complexity is reduced to O(m+n).[2]
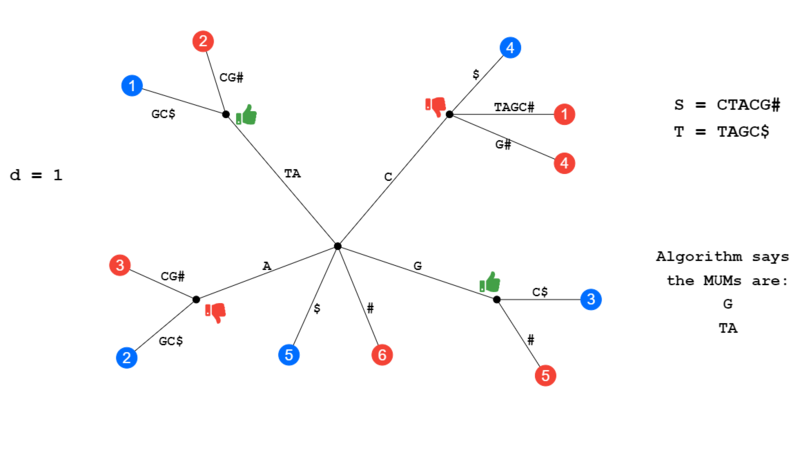
In the illustration below given the initial strings S and T and a d of 1, the MUMs should be G and TA. A red leaf denotes that the leaf came from string S and a blue leaf denotes string T. The internal node at A was discarded because A[i-1] = B[j-1] meaning the character that comes before both A's is identical (T), this is condition where the sequences belongs to a larger unique sequence. The internal node at C is discarded because it has two children from S. This leaves us with the MUMs of G and TA.
Example
[edit]To illustrate MUMs further, we take the following example. Let's say that d=3 and our two genomes are as follows:
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = CTGGTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
Working through the sequence our first MUM that satisfies the conditions occurs here:
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = CTGGTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
TGT is at least d in length, occurs only once in both sequences, and the characters to the left and right differ between genomes. To illustrate an example where expansion is needed to ensure that our MUM is not part of a larger sequence and unique, take the following:
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = CTGGTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
There are two problems in the case of testing ATG as a MUM because ATG is not unique and it is also part of a larger subsequence as illustrated here:
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = CTGGTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
Therefore expansion of this sequence is required in an attempt to satisfy the conditions for being a MUM as shown here.
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = CTGGTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
Using this method iteratively produces a final product where each MUM is identified for clarity each MUM is colored-coded:
S = CTACTGTCATGCTGAAGTCATGCGGCTGGCTTAT#
T = ACTTTGTGATGCTAAGTCATGCGGTCTGGCTTAT$
Maximal Exact Match (MEM)
[edit]MUMs are a subset of a larger set referred to as Maximal Exact Matches or MEMS. In a MEM the uniqueness condition of MUMs is relaxed. MEMs are like local alignment but in this case only identify sequences where there are no gaps.
See also
[edit]References
[edit]- ^ a b Delcher, A. L.; Kasif, S.; Fleishmann, R.D.; Peterson, J.; White, O.; Salzberg, S.L. (1999). "Alignment of whole genomes". Nucleic Acids Research. 27 (11): 2369–2376. doi:10.1093/nar/30.11.2478. PMC 117189. PMID 10325427.
- ^ a b c Wing-Kin, Sung (2010). Algorithms in Bioinformatics: A Practical Introduction (First ed.). Boca Raton: Chapman & Hall/CRC Press. ISBN 978-1420070330.
