Extended Wulff constructions
Extended Wulff constructions refer to a number of variants of the Wulff construction which is used for a solid single crystal in isolation.[1] They include cases for solid particle on substrates, those with twins and also when growth is important.[2] They are important for many applications such as supported metal nanoparticles used in heterogeneous catalysis or for understanding the shape of twinned nanoparticles being explored for other applications such as drug delivery or optical communications. They are also relevant for macroscopic crystals with twins. Depending upon whether there are twins or a substrate there are different cases as indicated in the decision tree figure.[3]
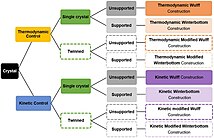
The simplest forms of these constructions yield the lowest free energy (thermodynamic) shape, or the stable form for a growing isolated particle; it can be difficult to differentiate between the two in experimental data. The thermodynamic cases involve the surface free energy of different facets; the term surface tension refers to liquids, not solids. Those during growth involve the growth velocity of the different surface facets.
While the thermodynamic and kinetic constructions are relevant for free standing particles, often in technological applications particles are on supports. An important case is heterogeneous catalysis where typically the surface of metal nanoparticles is where chemical reactions are taking place. To optimize the reactions a large metal surface area is desirable, but for stability the nanoparticles need to be supported on a substrate. The problem of the shape on a flat substrate is solved via the Winterbottom construction.
All the above are for single crystals, but it is common to have twins in the crystals. These can occur either by accident (growth twins), or can be an integral part of the structure as in decahedral or icosahedral particles. To understand the shape of particles with twin boundaries a Modified Wulff construction is used.
All these add some additional terms to the base Wulff construction. There are related constructions which have been proposed for other cases such as with alloying or when the interface between a nanoparticle and substrate is not flat.
General form
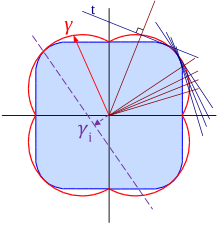
[edit]The thermodynamic Wulff describe the relationships between the shape of a single crystal and the surface free energy of different surfaces facets. It has the form that the perpendicular distance from a common center to all the external facets is proportional to the surface free energy of each one. This can be viewed as a relationship between the different surface energies and the distance from a Wulff center , where the vector is the "height" of the th face, drawn from the center to the face with a surface free energy of , and a scale. A common approach is to construct the planes normal to the vectors from the center to the surface free energy curve, with the Wulff shape the inner envelope. This is represented in the figure where the surface free energy is in red, and the single crystal shape would be in blue. In a more mathematical formalism it can be written describing the shape as a set of points given by[4][5]
for all unit vectors
For the extended constructions one or more additional terms are included for interface free energies, for instance the marked in purple with dashes in the figure. The dashed interface is included which may be a solid interface for the Winterbottom case, two interfaces for Summertop and or one, two or three twin boundaries for the modified Wulff construction. Comparable cases are generated when the surface free energy is replaced by a growth velocity, these applying for kinetic shapes.[2]
Winterbottom construction
[edit]
The Winterbottom construction, named after Walter L. Winterbottom,[6] is the solution for the shape of a solid particle on a fixed substrate, where the substrate is forced to remain flat. It is sometimes called the Kaischew-Winterbottom or Kaischew construction, since it was first analyzed for polyhedral shapes in a less general fashion by Kaischew[7] and later Ernst G. Bauer.[8] However, the proof by Winterbottom is more general.
The Winterbottom construction adds an extra term for the interface free energy which is assumed to stay flat. These shapes are found for nanoparticles supported on substrates such as in heterogeneous catalysis and also nanoparticle superlattices, and look similar to a truncated single particle, and can also resemble that of a liquid drop on a surface.[9][10] If the energy for the interface is very high then the particle has the same shape as it would have in isolation, and effectively dewets the substrate. If the energy is very low then a thin raft is formed on the substrate, it effectively wets the substrate.
The configuration found depends upon the orientation of the substrate, that of the particle as well as the relative orientation of the two. It is not uncommon to have more than one population of particle on substrate configurations in practice, each being a metastable energy minimum.[11] There is also some dependence upon whether there are steps, strain and anisotropy at the interface.[12][13][14] A related form has also been used for precipitates at boundaries, with semi-Wulff construction shapes on both sides.[15][16]
Summertop construction
[edit]This form was proposed as an extension of the Winterbottom construction (and a play on words) by Jean Taylor.[17] It applies to the case of a nanoparticle at a corner. Instead of just using one extra facet for the interface two are included. There are other related extensions, such as solutions in two dimensions for a crystal between two parallel planes.[18]
Modified Wulff construction
[edit]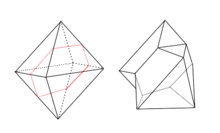
In many materials there are twins, which often correspond to a mirroring on a specific plane. For instance, a {111} plane for a face centered material such as gold is the normal twin plane. They often have re-entrant surfaces at the twin boundaries, a phenomenon reported in the 19th century and described in encyclopedias of crystal shapes.[20][21] The cases with one twin boundary are also called macle twins, although there can be more than one twin boundary.[21] An example of this called the Spinel law contact twinning is shown in the figure.[19] There can also be a series of parallel twins forming what are called Lamellar Twinned Particles,[22] which have been found in experimental samples both large and small.[23][24] For an odd number of boundaries these all resemble the macle twins; for an even number they are closer to single crystals.
There can also be two, non-parallel twin boundaries on each segment, a total of five twins in the composite particle, which leads to a shape that Cleveland and Uzi Landman called[25] a Marks decahedron when it occurs in face centered cubic materials with five units forming a fiveling cyclic twin.[26] There can also be three twin boundaries per segment where twenty units assemble to form an icosahedral structure. Both the decahedral and icosahedral forms can be the most stable ones at the nanoscale.[27] These forms occur for both elemental nanoparticles[28][29] as well as alloys[30][31] and colloidal crystals.[32][33]
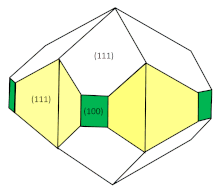
The approach to model these is similar to the Winterbottom construction, now adding an extra facet of energy per unit area half that of the twin boundary -- half so the energy per unit area of the two adjacent segments sums to a full twin boundary energy.[22][26] In many cases the twin boundary energy is small compared to an external surface energy,[35] so a single twin is close to half a single crystal rotated by 180 degrees, as observed experimentally. Five units then form a fiveling, which has reentrant surfaces at the twin boundaries and in shown in the figure, while for three boundaries per unit a close to perfect icosahedron is formed. The construction also predicts[22] more complicated shapes composed of combinations of decahedra, icosahedra and other complex twin-connected shapes, which have been observed experimentally in nanoparticles and were called polyparticles.[23] Other recent examples include bi-decahedra[36] and bi-icosahedra.[37] Extended combinations can lead to complex structures of overlapping five-fold structures in wires.[38]
While the earlier work was for crystals of materials such as silver and gold, more recently there has been work on colloidal cluster of nanoparticles where similar shapes have been observed,[32][33] although nonequilibrium shapes also occur.[39]
Kinetic Wulff construction
[edit]The thermodynamic Wulff and the others above describe the relationship between the shape of a single crystal and the surface free energy of different surfaces facets. It is named after Georg Wulff, but his paper[1] was not in fact on thermodynamics, rather on the growth kinetics. In many cases growth occurs via the nucleation of small islands on the surface then their sideways growth, either step-flow or layer-by-layer growth. The variant where this type growth dominates is the Kinetic Wulff construction.[40][41]
In the kinetic Wulff case the distance from the origin to each surface facet is proportional to the growth rate of the facet. This means that fast growing facets are often not present, for instance often {100} for a face centered cubic material; the external shape may be dominated by the slowest growing faces.[40] Note that other facets will reappear if the crystal is annealed when surface diffusion will change the shape towards the equilibrium shape. Most of the shapes in larger mineral crystals are a consequence of kinetic control. Both the surface free energy and growth rate of different surfaces depends strongly upon the presence of adsorbates, so can vary substantially.[42][43][44] Similar to the original work by Wulff, it is often unclear whether single crystals have a thermodynamic or kinetic Wulff shape.
There are analogues of all the earlier cases when kinetic control dominates:[45][2]
- Kinetic Winterbottom: the velocity replaces the surface energies for all the external facets, with the growth rate at the interface zero.[10]
- Kinetic Summertop: similar to the Winterbottom, with zero growth rate at the interfaces.[45]
- Kinetic Modified Wulff: the velocity replaces the surface energies for all the external facets, with zero growth velocity at the twin boundaries.[45] When kinetic growth dominates the velocity of the buried twin boundaries is zero. This can lead to cyclic twins with very sharp shapes.[45]
There can also be faster growth at re-entrant surfaces around twin boundaries,[46] at the interface for a Winterbottom case, at dislocations[47] and possibly at disclinations, all of which can lead to different shapes.[48] For instance, faster growth at twin boundaries leads to regular polyhedra such as pentagonal bipyramids for the fivelings with sharp corners and edges, and sharp icosahedral for the particles made of twenty subunits. The pentagonal bipyramids have been frequently observed in growth experiments, dating back to the early work by Shozo Ino and Shiro Ogawa in 1966-67,[49][50] and are not the thermodynamically stable stable but the kinetic one. Similar to the misinterpretation of the original paper by Wulff as mentioned above,[1] these sharp shapes have been misinterpreted as being part of the equilibrium shape.

For completeness, there is a different type of kinetic control of shapes called diffusion control,[52][53] which can lead to more complex shapes such as dendrites[54] and others.[39]
Related constructions
[edit]There are quite a few extensions and related constructions. Most of these to date are for relatively specialized cases. In particular:
- Strain at the particle-substrate interface can lead to changes which have been described in more generalized Winterbottom models[55] or by including a triple-line energy term;[56] the latter has been observed experimentally.[56]
- Modified forms have been developed when there are steps, as this can introduce strain.[57]
- A more complex variational approach can be used to model alloy nanoparticles[58] or when combining the twin-variant and a substrate.[59]
- While the most common use of these constructions are in three dimensions for particles, they can also be used to understand two-dimensional growth shapes,[60] grain boundary faceting,[61] voids[62] when the interface is anisotropic,[12][63] and for dislocations.[64]
Caveats
[edit]
These variants of the Wulff construction correlate well to many shapes found experimentally, but do not explain everything. Sometimes the shapes with multiple different units are due to coalescence, sometimes they are less symmetric and sometimes, as in Janus particles (for the two-headed god) they contain two materials.[65] There are also some assumptions such as that the substrate remains flat in the Winter bottom construction. This does not have to be the case, the particle can partially or completely be buried by the substrate.[2]
It can also be the case that metastable structures are formed.[39] For instance during growth at elevated temperatures a neck can form between two particles, and they can start to merge.[66] If the temperature is decreased then diffusion can become slow so this shape can persist.[67]
Finally, the descriptions here work well for particles of size about 5nm and larger. At smaller sizes more local bonding can become important, so nanoclusters of more limited sizes can be more complex.[68][69]
Application relevance
[edit]Heterogeneous catalysts
[edit]These contain nanoparticles on a support, where either the nanoparticles or combination plays a key role in speeding up a chemical reaction. The support can also play a role in reducing sintering by stabilizing the particles so there is less reduction in their surface area with extended use -- larger particles produced by sintering small ones have less surface area for the same total number of atoms.[70]
In addition, the substrate can determine the orientation of the nanoparticles, and combined with what surfaces are exposed in the Winterbottom construction there can be different reactivities which has been exploited for prototype catalysts.[71][72][73][74]
Nucleation
[edit]At small sizes, particularly for face centered cubic materials cyclic twins called multiply twinned particles are often of lower energy than single crystals. The main reason is that they have more lower energy surfaces, mainly (111).[26] This is balanced by elastic deformation which raises the energy.[75] At small sizes the surface energy dominated so icosahedral particles are lowest in energy. As the size increases the decahedral ones become lowest in energy, then at the largest size it is single crystals. The decahedral particles and, to a lesser extent the icosahedral ones have shapes determined by the Modified Wulff construction.[2] Note that due to the discrete nature of atoms there can be deviations from the continuum shapes at very small sizes.[76]
Plasmonics
[edit]The optical response of nanoparticles depends upon their shape, size and the materials.[77] For instance, rod shapes which are very anisotropic can be grown using decahedral seeds if the growth on (100) facets is slow, a kinetic Wulff shapes. These have quite different optical responses than icosahedra, which are close to spherical, while cubes can also be produced if the (111) growth rate is very fast, and these have yet further optical responses.[78][79][80]

Minerals
[edit]As alluded to earlier, many minerals have crystal twins, and these approaches provide methods to explain the morphologies for either kinetic or thermodynamic control for shapes found in the literature[19] for in marcasite,[81][82] and by Gustav Rose in 1831 for gold.[83][84]
See Also
[edit]- Chemical physics – Subdiscipline of chemistry and physics
- Cluster (chemistry) – Collection of bound atoms or molecules
- Cluster (physics) – Small collection of atoms or molecules
- Crystal habit – Mineralogical term for the visible shape of a mineral
- Crystal twinning – Two separate crystals sharing some of the same crystal lattice points in a symmetrical manner
- Disclination – Angular defect in a material
- Icosahedral twins – Structure found in atomic clusters and nanoparticles
- Nanocluster – Collection of bound atoms or molecules
- Nanomaterials – Materials whose granular size lies between 1 and 100 nm
- Nanowire – Wire with a diameter in the nanometres
- Nucleation – Initial step in the phase transition or molecular self-assembly of a substance
- Surface energy – Excess energy at the surface of a material relative to its interior
- Surface stress – Change of surface energy with strain
- Wulff construction – Lowest energy shape of a single crystal
References
[edit]- ^ a b c Wulff, G. (1901). "XXV. Zur Frage der Geschwindigkeit des Wachsthums und der Auflösung der Krystallflächen". Zeitschrift für Kristallographie - Crystalline Materials. 34 (1–6): 449–530. doi:10.1524/zkri.1901.34.1.449. ISSN 2196-7105.
- ^ a b c d e Marks, L D; Peng, L (2016-02-10). "Nanoparticle shape, thermodynamics and kinetics". Journal of Physics: Condensed Matter. 28 (5): 053001. Bibcode:2016JPCM...28e3001M. doi:10.1088/0953-8984/28/5/053001. ISSN 0953-8984. PMID 26792459.
- ^ a b Boukouvala, Christina; Daniel, Joshua; Ringe, Emilie (2021-09-09). "Approaches to modelling the shape of nanocrystals". Nano Convergence. 8 (1): 26. Bibcode:2021NanoC...8...26B. doi:10.1186/s40580-021-00275-6. ISSN 2196-5404. PMC 8429535. PMID 34499259.
- ^ Cahn, J.l; Hoffman, D.l (1974). "A vector thermodlnamics for anisotropic surfaces—II. Curved and faceted surfaces". Acta Metallurgica. 22 (10): 1205–1214. doi:10.1016/0001-6160(74)90134-5.
- ^ Hoffman, David W.; Cahn, John W. (1972). "A vector thermodynamics for anisotropic surfaces". Surface Science. 31: 368–388. doi:10.1016/0039-6028(72)90268-3.
- ^ Winterbottom, W.L (1967). "Equilibrium shape of a small particle in contact with a foreign substrate". Acta Metallurgica. 15 (2): 303–310. doi:10.1016/0001-6160(67)90206-4. ISSN 0001-6160.
- ^ Kaischew, R (1952). Arbeitstagung Festkörper Physik. Dresden: Verlag. p. 81.
- ^ Bauer, Ernst (January 1958). "Phänomenologische Theorie der Kristallabscheidung an Oberflächen. I". Zeitschrift für Kristallographie. 110 (1–6): 372–394. Bibcode:1958ZK....110..372B. doi:10.1524/zkri.1958.110.1-6.372. ISSN 0044-2968.
- ^ Enterkin, James A.; Poeppelmeier, Kenneth R.; Marks, Laurence D. (2011-03-09). "Oriented Catalytic Platinum Nanoparticles on High Surface Area Strontium Titanate Nanocuboids". Nano Letters. 11 (3): 993–997. Bibcode:2011NanoL..11..993E. doi:10.1021/nl104263j. ISSN 1530-6984. PMID 21288039.
- ^ a b Lewis, Diana J.; Zornberg, Leonardo Z.; Carter, David J. D.; Macfarlane, Robert J. (July 2020). "Single-crystal Winterbottom constructions of nanoparticle superlattices". Nature Materials. 19 (7): 719–724. Bibcode:2020NatMa..19..719L. doi:10.1038/s41563-020-0643-6. hdl:1721.1/127785. ISSN 1476-1122. PMID 32203459.
- ^ Bao, Weizhu; Jiang, Wei; Srolovitz, David J.; Wang, Yan (2017). "Stable Equilibria of Anisotropic Particles on Substrates: A Generalized Winterbottom Construction". SIAM Journal on Applied Mathematics. 77 (6): 2093–2118. arXiv:1608.08481. doi:10.1137/16M1091599. ISSN 0036-1399.
- ^ a b Siem, Ellen J.; Carter ‡, W. Craig; Chatain §, Dominique (April 2004). "The equilibrium shape of anisotropic interfacial particles". Philosophical Magazine. 84 (10): 991–1010. Bibcode:2004PMag...84..991S. doi:10.1080/14786430310001639897. ISSN 1478-6435.
- ^ Sivaramakrishnan, Shankar; Wen, Jianguo; Scarpelli, Michael. E.; Pierce, Benjamin J.; Zuo, Jian-Min (2010-11-10). "Equilibrium shapes and triple line energy of epitaxial gold nanocrystals supported on TiO 2 ( 110 )". Physical Review B. 82 (19): 195421. doi:10.1103/PhysRevB.82.195421. ISSN 1098-0121.
- ^ Müller, P.; Kern, R. (1998). "Equilibrium shape of epitaxially strained crystals (Volmer–Weber case)". Journal of Crystal Growth. 193 (1–2): 257–270. Bibcode:1998JCrGr.193..257M. doi:10.1016/S0022-0248(98)00508-9.
- ^ Zucker, Rachel V.; Chatain, Dominique; Dahmen, Ulrich; Hagège, Serge; Carter, W. Craig (2012). "New software tools for the calculation and display of isolated and attached interfacial-energy minimizing particle shapes". Journal of Materials Science. 47 (24): 8290–8302. Bibcode:2012JMatS..47.8290Z. doi:10.1007/s10853-012-6739-x. ISSN 0022-2461.
- ^ Zucker, Rachel V. (Rachel Victoria) (2015). Capillary-driven shape evolution in solid-state micro- and nano-scale systems (Thesis thesis). Massachusetts Institute of Technology. hdl:1721.1/98575.
- ^ Zia, R. K. P.; Avron, J. E.; Taylor, J. E. (1988). "The summertop construction: Crystals in a corner". Journal of Statistical Physics. 50 (3–4): 727–736. Bibcode:1988JSP....50..727Z. doi:10.1007/BF01026498. ISSN 0022-4715.
- ^ De Coninck, J.; Fruttero, J.; Ziermann, A. (1994). "The equilibrium shape of a two-dimensional crystal between parallel planes". Journal of Statistical Physics. 74 (5–6): 1255–1264. Bibcode:1994JSP....74.1255D. doi:10.1007/bf02188228. ISSN 0022-4715.
- ^ a b c Sinkankas, John (1964). Mineralogy for amateurs. Princeton, N.J.: Van Nostrand. pp. 96–105. ISBN 0442276249.
- ^ Comte de Bournon, Jacques-Louis (1813). Catalogue de la collection minéralogique du comte de Bournon,... faites par lui-même . Et dans lequel sont placés plusieurs observations et faits intéressants... ainsi qu'une réponse au mémoire de M. l'abbé Haüy concernant la simplicité des lois auxquelles est soumise la structure des cristaux, etc. L. Deconchy.
- ^ a b Collins, Joseph Henry (1878). Mineralogy. With ... Illustrations, Volym 1. National Library of Scotland. p. 120.
- ^ a b c Marks, L.D. (1983). "Modified Wulff constructions for twinned particles". Journal of Crystal Growth. 61 (3): 556–566. Bibcode:1983JCrGr..61..556M. doi:10.1016/0022-0248(83)90184-7.
- ^ a b Smith, David J.; Marks, L.D. (September 1981). "High resolution studies of small particles of gold and silver". Journal of Crystal Growth. 54 (3): 433–438. doi:10.1016/0022-0248(81)90495-4.
- ^ Gontard, L. C.; Dunin-Borkowski, R. E.; Gass, M. H.; Bleloch, A. L.; Ozkaya, D. (2009-06-01). "Three-dimensional shapes and structures of lamellar-twinned fcc nanoparticles using ADF STEM". Journal of Electron Microscopy. 58 (3): 167–174. doi:10.1093/jmicro/dfp003. ISSN 0022-0744. PMID 19211653.
- ^ Cleveland, Charles L.; Landman, Uzi (1991). "The energetics and structure of nickel clusters: Size dependence". The Journal of Chemical Physics. 94 (11): 7376–7396. Bibcode:1991JChPh..94.7376C. doi:10.1063/1.460169. ISSN 0021-9606.
- ^ a b c Marks, L. D. (1984). "Surface structure and energetics of multiply twinned particles". Philosophical Magazine A. 49 (1): 81–93. Bibcode:1984PMagA..49...81M. doi:10.1080/01418618408233431. ISSN 0141-8610.
- ^ Howie, A.; Marks, L. D. (1984). "Elastic strains and the energy balance for multiply twinned particles". Philosophical Magazine A. 49 (1): 95–109. Bibcode:1984PMagA..49...95H. doi:10.1080/01418618408233432. ISSN 0141-8610.
- ^ Zhang, Qingbo; Xie, Jianping; Yang, Jinhua; Lee, Jim Yang (2009-01-27). "Monodisperse Icosahedral Ag, Au, and Pd Nanoparticles: Size Control Strategy and Superlattice Formation". ACS Nano. 3 (1): 139–148. doi:10.1021/nn800531q. ISSN 1936-0851. PMID 19206260.
- ^ Wang, Helan; Zhou, Shan; Gilroy, Kyle D.; Cai, Zaisheng; Xia, Younan (2017-08-01). "Icosahedral nanocrystals of noble metals: Synthesis and applications". Nano Today. 15: 121–144. doi:10.1016/j.nantod.2017.06.011. ISSN 1748-0132.
- ^ Akbarzadeh, Hamed; Abbaspour, Mohsen; Mehrjouei, Esmat (2017-09-01). "Au@Pt and Pt@Au nanoalloys in the icosahedral and cuboctahedral structures: Which is more stable?". Journal of Molecular Liquids. 242: 1002–1017. doi:10.1016/j.molliq.2017.07.096. ISSN 0167-7322.
- ^ Wu, Jianbo; Qi, Liang; You, Hongjun; Gross, Adam; Li, Ju; Yang, Hong (2012-07-25). "Icosahedral Platinum Alloy Nanocrystals with Enhanced Electrocatalytic Activities". Journal of the American Chemical Society. 134 (29): 11880–11883. Bibcode:2012JAChS.13411880W. doi:10.1021/ja303950v. ISSN 0002-7863. PMID 22738173.
- ^ a b Ohnuki, Ryosuke; Takeoka, Yukikazu; Yoshioka, Shinya (2024-03-26). "Structural and Optical Characterization of Decahedral-Type Spherical Colloidal Clusters". Chemistry of Materials. 36 (6): 2953–2962. doi:10.1021/acs.chemmater.3c03306. ISSN 0897-4756.
- ^ a b Xu, Meng; Kim, Eun Ji; Lee, Young Jun; Lee, Hyunsoo; Jung, Kyunghyun; Choi, Jaeyoung; Kim, Shin-Hyun; Kim, YongJoo; Yun, Hongseok; Kim, Bumjoon J. (2024-06-14). "Icosahedral supracrystal assembly from polymer-grafted nanoparticles via interplay of interfacial energy and confinement effect". Science Advances. 10 (24): eado0745. Bibcode:2024SciA...10O.745X. doi:10.1126/sciadv.ado0745. PMC 11177942. PMID 38875331.
- ^ Rose, Gustav (1831). "Ueber die Krystallformen des Goldes und des Silbers". Annalen der Physik. 99 (10): 196–204. Bibcode:1831AnP....99..196R. doi:10.1002/andp.18310991003. ISSN 0003-3804.
- ^ Rohrer, Gregory S. (2011). "Grain boundary energy anisotropy: a review". Journal of Materials Science. 46 (18): 5881–5895. Bibcode:2011JMatS..46.5881R. doi:10.1007/s10853-011-5677-3. ISSN 0022-2461.
- ^ Koga, Kenji (2006-03-21). "Novel Bidecahedral Morphology in Gold Nanoparticles Frozen from Liquid". Physical Review Letters. 96 (11): 115501. Bibcode:2006PhRvL..96k5501K. doi:10.1103/PhysRevLett.96.115501. ISSN 0031-9007. PMID 16605837.
- ^ Nepijko, S.A.; Hofmeister, H.; Sack-Kongehl, H.; Schlögl, R. (May 2000). "Multiply twinned particles beyond the icosahedron". Journal of Crystal Growth. 213 (1–2): 129–134. Bibcode:2000JCrGr.213..129N. doi:10.1016/S0022-0248(00)00337-7.
- ^ Velázquez-Salazar, J. Jesús; Esparza, Rodrigo; Mejía-Rosales, Sergio Javier; Estrada-Salas, Rubén; Ponce, Arturo; Deepak, Francis Leonard; Castro-Guerrero, Carlos; José-Yacamán, Miguel (2011-08-23). "Experimental Evidence of Icosahedral and Decahedral Packing in One-Dimensional Nanostructures". ACS Nano. 5 (8): 6272–6278. doi:10.1021/nn202495r. ISSN 1936-0851. PMC 3180901. PMID 21790155.
- ^ a b c Ye, Matthew; Hueckel, Theodore; Gatenil, Perapat P.; Nagao, Keisuke; Carter, W. Craig; Macfarlane, Robert J. (2024-06-18). "Nanoparticle Superlattices with Nonequilibrium Crystal Shapes". ACS Nano. 18 (24): 15970–15977. doi:10.1021/acsnano.4c04192. ISSN 1936-0851. PMID 38838258.
- ^ a b Sekerka, Robert F. (2005). "Equilibrium and growth shapes of crystals: how do they differ and why should we care?". Crystal Research and Technology. 40 (4–5): 291–306. Bibcode:2005CryRT..40..291S. doi:10.1002/crat.200410342. ISSN 0232-1300.
- ^ Sun, Qian; Yerino, Christopher D.; Leung, Benjamin; Han, Jung; Coltrin, Michael E. (2011-09-01). "Understanding and controlling heteroepitaxy with the kinetic Wulff plot: A case study with GaN". Journal of Applied Physics. 110 (5): 053517–053517–10. Bibcode:2011JAP...110e3517S. doi:10.1063/1.3632073. ISSN 0021-8979.
- ^ Leung, T. C.; Kao, C. L.; Su, W. S.; Feng, Y. J.; Chan, C. T. (2003-11-17). "Relationship between surface dipole, work function and charge transfer: Some exceptions to an established rule". Physical Review B. 68 (19): 195408. Bibcode:2003PhRvB..68s5408L. doi:10.1103/PhysRevB.68.195408. ISSN 0163-1829.
- ^ Löfgren, Joakim; Rahm, J. Magnus; Brorsson, Joakim; Erhart, Paul (2020-09-14). "Computational assessment of the efficacy of halides as shape-directing agents in nanoparticle growth". Physical Review Materials. 4 (9): 096001. arXiv:2006.07068. Bibcode:2020PhRvM...4i6001L. doi:10.1103/PhysRevMaterials.4.096001. ISSN 2475-9953.
- ^ Fichthorn, Kristen A.; Balankura, Tonnam; Qi, Xin (2016). "Multi-scale theory and simulation of shape-selective nanocrystal growth". CrystEngComm. 18 (29): 5410–5417. doi:10.1039/C6CE01012A. ISSN 1466-8033.
- ^ a b c d Ringe, Emilie; Van Duyne, Richard P.; Marks, Laurence D. (2013). "Kinetic and Thermodynamic Modified Wulff Constructions for Twinned Nanoparticles". The Journal of Physical Chemistry C. 117 (31): 15859–15870. doi:10.1021/jp401566m. ISSN 1932-7447.
- ^ Shahani, Ashwin J.; Gulsoy, E. Begum; Poulsen, Stefan O.; Xiao, Xianghui; Voorhees, Peter W. (2016-06-27). "Twin-mediated crystal growth: an enigma resolved". Scientific Reports. 6 (1): 28651. Bibcode:2016NatSR...628651S. doi:10.1038/srep28651. ISSN 2045-2322. PMC 4922011. PMID 27346073.
- ^ Meng, Fei; Morin, Stephen A.; Forticaux, Audrey; Jin, Song (2013-07-16). "Screw Dislocation Driven Growth of Nanomaterials". Accounts of Chemical Research. 46 (7): 1616–1626. doi:10.1021/ar400003q. ISSN 0001-4842. PMID 23738750.
- ^ Cui, Jianming; Phul, Saksham; Fichthorn, Kristen A. (2023-04-28). "Diffusion growth mechanism of penta-twinned Ag nanocrystals from decahedral seeds". The Journal of Chemical Physics. 158 (16). Bibcode:2023JChPh.158p4707C. doi:10.1063/5.0146305. ISSN 0021-9606. OSTI 2395911. PMID 37093141.
- ^ Ino, Shozo (1966). "Epitaxial Growth of Metals on Rocksalt Faces Cleaved in Vacuum. II. Orientation and Structure of Gold Particles Formed in Ultrahigh Vacuum". Journal of the Physical Society of Japan. 21 (2): 346–362. Bibcode:1966JPSJ...21..346I. doi:10.1143/JPSJ.21.346. ISSN 0031-9015.
- ^ Ino, Shozo; Ogawa, Shiro (1967). "Multiply Twinned Particles at Earlier Stages of Gold Film Formation on Alkalihalide Crystals". Journal of the Physical Society of Japan. 22 (6): 1365–1374. Bibcode:1967JPSJ...22.1365I. doi:10.1143/JPSJ.22.1365. ISSN 0031-9015.
- ^ Bazán-Díaz, Lourdes; Mendoza-Cruz, Rubén; Velázquez-Salazar, J. Jesús; Plascencia-Villa, Germán; Romeu, David; Reyes-Gasga, José; Herrera-Becerra, Raúl; José-Yacamán, Miguel; Guisbiers, Grégory (2015). "Gold–copper nanostars as photo-thermal agents: synthesis and advanced electron microscopy characterization". Nanoscale. 7 (48): 20734–20742. Bibcode:2015Nanos...720734B. doi:10.1039/C5NR06491K. ISSN 2040-3364. PMID 26602429.
- ^ Ben-Jacob, Eshel; Garik, Peter (February 1990). "The formation of patterns in non-equilibrium growth". Nature. 343 (6258): 523–530. Bibcode:1990Natur.343..523B. doi:10.1038/343523a0. hdl:2027.42/62774. ISSN 0028-0836.
- ^ Brener, E; Müller-Krumbhaar, H; Temkin, D (1992-02-01). "Kinetic Phase Diagram and Scaling Relations for Stationary Diffusional Growth". Europhysics Letters (EPL). 17 (6): 535–540. Bibcode:1992EL.....17..535B. doi:10.1209/0295-5075/17/6/010. ISSN 0295-5075.
- ^ Huang, S.-C.; Glicksman, M.E. (1981). "Overview 12: Fundamentals of dendritic solidification—I. Steady-state tip growth". Acta Metallurgica. 29 (5): 701–715. doi:10.1016/0001-6160(81)90115-2. ISSN 0001-6160.
- ^ Müller, P.; Kern, R. (1998). "Equilibrium shape of epitaxially strained crystals (Volmer–Weber case)". Journal of Crystal Growth. 193 (1–2): 257–270. Bibcode:1998JCrGr.193..257M. doi:10.1016/S0022-0248(98)00508-9.
- ^ a b Sivaramakrishnan, Shankar; Wen, Jianguo; Scarpelli, Michael. E.; Pierce, Benjamin J.; Zuo, Jian-Min (2010-11-10). "Equilibrium shapes and triple line energy of epitaxial gold nanocrystals supported on TiO 2 ( 110 )". Physical Review B. 82 (19): 195421. doi:10.1103/PhysRevB.82.195421. ISSN 1098-0121.
- ^ Gao, Wenpei; Choi, Ann Se; Zuo, Jian-Min (July 2014). "Interaction of nanometer-sized gold nanocrystals with rutile (110) surface steps revealed at atomic resolution". Surface Science. 625: 16–22. Bibcode:2014SurSc.625...16G. doi:10.1016/j.susc.2014.02.016.
- ^ Ringe, E.; Van Duyne, R. P.; Marks, L. D. (2011-08-10). "Wulff Construction for Alloy Nanoparticles". Nano Letters. 11 (8): 3399–3403. Bibcode:2011NanoL..11.3399R. doi:10.1021/nl2018146. ISSN 1530-6984. PMID 21744799.
- ^ Mansley, Zachary R.; Marks, Laurence D. (2020-12-24). "Modified Winterbottom Construction Including Boundaries". The Journal of Physical Chemistry C. 124 (51): 28038–28043. doi:10.1021/acs.jpcc.0c07316. ISSN 1932-7447. OSTI 1778933.
- ^ Giesen, Margret; Steimer, Christoph; Ibach, Harald (January 2001). "What does one learn from equilibrium shapes of two-dimensional islands on surfaces?". Surface Science. 471 (1–3): 80–100. Bibcode:2001SurSc.471...80G. doi:10.1016/S0039-6028(00)00888-8.
- ^ Straumal, B.B.; Polyakov, S.A.; Bischoff, E.; Gust, W.; Mittemeijer, E.J. (2001). "Faceting of Sigma-3 and Sigma-9 grain boundaries in copper". Interface Science. 9 (3/4): 287–292. doi:10.1023/A:1015174921561.
- ^ Siegel, M (2004). "Evolution of material voids for highly anisotropic surface energy". Journal of the Mechanics and Physics of Solids. 52 (6): 1319–1353. Bibcode:2004JMPSo..52.1319S. doi:10.1016/j.jmps.2003.11.003.
- ^ Bao, Weizhu; Jiang, Wei; Srolovitz, David J.; Wang, Yan (2017). "Stable Equilibria of Anisotropic Particles on Substrates: A Generalized Winterbottom Construction". SIAM Journal on Applied Mathematics. 77 (6): 2093–2118. arXiv:1608.08481. doi:10.1137/16M1091599. ISSN 0036-1399.
- ^ Hazzledine, P. M.; Karnthaler, H. P.; Korner, A. (1984-02-16). "The Application of the Wulff Construction to Dislocation Problems". Physica Status Solidi (A). 81 (2): 473–484. Bibcode:1984PSSAR..81..473H. doi:10.1002/pssa.2210810209.
- ^ Walther, Andreas; Müller, Axel H. E. (2013-07-10). "Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications". Chemical Reviews. 113 (7): 5194–5261. doi:10.1021/cr300089t. ISSN 0009-2665. PMID 23557169.
- ^ Nelli, Diana; Rossi, Giulia; Wang, Zhiwei; Palmer, Richard E.; Ferrando, Riccardo (2020). "Structure and orientation effects in the coalescence of Au clusters". Nanoscale. 12 (14): 7688–7699. doi:10.1039/C9NR10163B. ISSN 2040-3364. PMID 32211622.
- ^ Combe, Nicolas; Jensen, Pablo; Pimpinelli, Alberto (2000-07-03). "Changing Shapes in the Nanoworld". Physical Review Letters. 85 (1): 110–113. arXiv:cond-mat/0005113. Bibcode:2000PhRvL..85..110C. doi:10.1103/PhysRevLett.85.110. ISSN 0031-9007. PMID 10991171.
- ^ Wales, David J.; Doye, Jonathan P. K.; Miller, Mark A.; Mortenson, Paul N.; Walsh, Tiffany R. (January 2000), Prigogine, I.; Rice, Stuart A. (eds.), "Energy Landscapes: From Clusters to Biomolecules", Advances in Chemical Physics, vol. 115 (1 ed.), Wiley, pp. 1–111, doi:10.1002/9780470141748.ch1, ISBN 978-0-471-39331-3, retrieved 2025-01-12
- ^ Mottet, C.; Goniakowski, J.; Baletto, F.; Ferrando, R.; Treglia, G. (2004-01-01). "Modeling free and supported metallic nanoclusters: structure and dynamics". Phase Transitions. 77 (1–2): 101–113. Bibcode:2004PhaTr..77..101M. doi:10.1080/1411590310001622473. ISSN 0141-1594.
- ^ Hemmingson, Stephanie L.; Campbell, Charles T. (2017-02-28). "Trends in Adhesion Energies of Metal Nanoparticles on Oxide Surfaces: Understanding Support Effects in Catalysis and Nanotechnology". ACS Nano. 11 (2): 1196–1203. doi:10.1021/acsnano.6b07502. ISSN 1936-0851. OSTI 1534920. PMID 28045491.
- ^ Boucher, Matthew B.; Goergen, Simone; Yi, Nan; Flytzani-Stephanopoulos, Maria (2011). "'Shape effects' in metal oxide supported nanoscale gold catalysts". Physical Chemistry Chemical Physics. 13 (7): 2517–2527. Bibcode:2011PCCP...13.2517B. doi:10.1039/c0cp02009e. ISSN 1463-9076. PMID 21240451.
- ^ Enterkin, James A.; Kennedy, Robert M.; Lu, Junling; Elam, Jeffrey W.; Cook, Russell E.; Marks, Laurence D.; Stair, Peter C.; Marshall, Christopher L.; Poeppelmeier, Kenneth R. (2013). "Epitaxial Stabilization of Face Selective Catalysts". Topics in Catalysis. 56 (18–20): 1829–1834. doi:10.1007/s11244-013-0118-y. ISSN 1022-5528.
- ^ Wu, Zili; Mann, Amanda K. P.; Li, Meijun; Overbury, Steven H. (2015-04-02). "Spectroscopic Investigation of Surface-Dependent Acid–Base Property of Ceria Nanoshapes". The Journal of Physical Chemistry C. 119 (13): 7340–7350. doi:10.1021/acs.jpcc.5b00859. ISSN 1932-7447. OSTI 1185894.
- ^ Trovarelli, Alessandro; Llorca, Jordi (2017-07-07). "Ceria Catalysts at Nanoscale: How Do Crystal Shapes Shape Catalysis?". ACS Catalysis. 7 (7): 4716–4735. doi:10.1021/acscatal.7b01246. hdl:2117/107674. ISSN 2155-5435.
- ^ Wu, Hsin-Lun; Tsai, Huei-Ru; Hung, Yun-Ting; Lao, Ka-Un; Liao, Ching-Wen; Chung, Pei-Ju; Huang, Jer-Shing; Chen, I-Chia; Huang, Michael H. (2011-09-05). "A Comparative Study of Gold Nanocubes, Octahedra, and Rhombic Dodecahedra as Highly Sensitive SERS Substrates". Inorganic Chemistry. 50 (17): 8106–8111. doi:10.1021/ic200504n. ISSN 0020-1669. PMID 21797229.
- ^ Jiang; Cai; Shao (2003-05-01). "New Lowest Energy Sequence of Marks' Decahedral Lennard-Jones Clusters Containing up to 10 000 Atoms". The Journal of Physical Chemistry A. 107 (21): 4238–4243. Bibcode:2003JPCA..107.4238J. doi:10.1021/jp0342327. ISSN 1089-5639.
- ^ Ringe, Emilie (2020-07-23). "Shapes, Plasmonic Properties, and Reactivity of Magnesium Nanoparticles". The Journal of Physical Chemistry C. 124 (29): 15665–15679. doi:10.1021/acs.jpcc.0c03871. ISSN 1932-7447. PMC 7467285. PMID 32905178.
- ^ Zhang, W. C.; Wu, X. L.; Kan, C. X.; Pan, F. M.; Chen, H. T.; Zhu, J.; Chu, Paul K. (2010). "Surface-enhanced Raman scattering from silver nanostructures with different morphologies". Applied Physics A. 100 (1): 83–88. Bibcode:2010ApPhA.100...83Z. doi:10.1007/s00339-010-5583-6. ISSN 0947-8396.
- ^ Halas, Naomi J.; Lal, Surbhi; Chang, Wei-Shun; Link, Stephan; Nordlander, Peter (2011-06-08). "Plasmons in Strongly Coupled Metallic Nanostructures". Chemical Reviews. 111 (6): 3913–3961. doi:10.1021/cr200061k. ISSN 0009-2665. PMID 21542636.
- ^ Wu, Hsin-Lun; Tsai, Huei-Ru; Hung, Yun-Ting; Lao, Ka-Un; Liao, Ching-Wen; Chung, Pei-Ju; Huang, Jer-Shing; Chen, I-Chia; Huang, Michael H. (2011-09-05). "A Comparative Study of Gold Nanocubes, Octahedra, and Rhombic Dodecahedra as Highly Sensitive SERS Substrates". Inorganic Chemistry. 50 (17): 8106–8111. doi:10.1021/ic200504n. ISSN 0020-1669. PMID 21797229.
- ^ Comte de Bournon, Jacques-Louis (1813). Catalogue de la collection minéralogique du comte de Bournon,... faites par lui-même . Et dans lequel sont placés plusieurs observations et faits intéressants... ainsi qu'une réponse au mémoire de M. l'abbé Haüy concernant la simplicité des lois auxquelles est soumise la structure des cristaux, etc. L. Deconchy. pp. 301–308.
- ^ Comte de Bournon, Jacques-Louis (1813). Catalogue de la collection minéralogique du comte de Bournon,... faites par lui-même . Et dans lequel sont placés plusieurs observations et faits intéressants... ainsi qu'une réponse au mémoire de M. l'abbé Haüy concernant la simplicité des lois auxquelles est soumise la structure des cristaux, etc. L. Deconchy. pp. plates VIII and esp. IX, fig 164–168.
- ^ Rose, Gustav (1831). "Ueber die Krystallformen des Goldes und des Silbers". Annalen der Physik. 99 (10): 196–204. Bibcode:1831AnP....99..196R. doi:10.1002/andp.18310991003. ISSN 0003-3804.
- ^ Kvasnifsa, V. N.; Kuznetsov, Yu. A.; Latysh, I. K. (1981). "Crystal morphology of native gold from some ore regions of the Ukraine". International Geology Review. 23 (2): 227–232 Figure 5. Bibcode:1981IGRv...23..227K. doi:10.1080/00206818209467235. ISSN 0020-6814.
External links
[edit]- "Crystal creator code". www.on.msm.cam.ac.uk. Retrieved 2024-04-01. Code from the group of Emilie Ringe which calculates thermodynamic and kinetic shapes for decahedral particles and also does optical simulations, see also Boukouvala, Christina; Ringe, Emilie (2019-10-17). "Wulff-Based Approach to Modeling the Plasmonic Response of Single Crystal, Twinned, and Core–Shell Nanoparticles". The Journal of Physical Chemistry C. 123 (41): 25501–25508. doi:10.1021/acs.jpcc.9b07584. ISSN 1932-7447. PMC 6822593. PMID 31681455.
- Roosen, Andrew R; McCormack, Ryan P; Carter, W.Craig (1998). "Wulffman: A tool for the calculation and display of crystal shapes". Computational Materials Science. 11 (1): 16–26. doi:10.1016/S0927-0256(97)00167-5. Code for Wulff and Winterbottom shapes.
- Zucker, Rachel V.; Chatain, Dominique; Dahmen, Ulrich; Hagège, Serge; Carter, W. Craig (2012). "New software tools for the calculation and display of isolated and attached interfacial-energy minimizing particle shapes". Journal of Materials Science. 47 (24): 8290–8302. Bibcode:2012JMatS..47.8290Z. doi:10.1007/s10853-012-6739-x. ISSN 0022-2461. Updated information on Wulffman, including double Winterbottom shapes,
- "WulffPack – a package for Wulff constructions". wulffpack.materialsmodeling.org. Retrieved 2024-04-01. Code from J M Rahm and P Erhart which calculates thermodynamic shapes, both continuum and atomistic, see also Rahm, J.; Erhart, Paul (2020). "WulffPack: A Python package for Wulff constructions". Journal of Open Source Software. 5 (45): 1944. Bibcode:2020JOSS....5.1944R. doi:10.21105/joss.01944. ISSN 2475-9066..
- "Shape Software". www.shapesoftware.com. Retrieved 2024-05-09. The code can be used to generate thermodynamic Wulff shapes including twinning.










