Draft:Arrangement of pseudolines
 | Review waiting, please be patient.
This may take 2 months or more, since drafts are reviewed in no specific order. There are 2,351 pending submissions waiting for review.
Where to get help
How to improve a draft
You can also browse Wikipedia:Featured articles and Wikipedia:Good articles to find examples of Wikipedia's best writing on topics similar to your proposed article. Improving your odds of a speedy review To improve your odds of a faster review, tag your draft with relevant WikiProject tags using the button below. This will let reviewers know a new draft has been submitted in their area of interest. For instance, if you wrote about a female astronomer, you would want to add the Biography, Astronomy, and Women scientists tags. Editor resources
Reviewer tools
|
Comment: Can you provide more information for the sources? At present, a reader cannot figure out the source cited because not enough information is provided. For instance, you need to provide titles and publications (e.g., journal, book, or website title). Significa liberdade (she/her) (talk) 10:08, 17 February 2025 (UTC)
An arrangement of pseudolines is a family of curves that share similar topological properties with a line arrangement.[1] Most commonly, in the study of arrangements of lines, these have the simple property that each crosses every other line exactly once. These can be defined in the projective plane as simple closed curves any two of which meet in a single crossing point.[2] A pseudoline arrangement is said to be stretchable if it is combinatorially equivalent to a line arrangement, meaning that you can straighten each one while maintaining the order in which each crosses each other. Determining stretchability is a difficult computational task: it is complete for the existential theory of the reals to distinguish stretchable arrangements from non-stretchable ones.[3] Every arrangement of finitely many pseudolines can be extended so that they become lines in a "spread", a type of non-Euclidean incidence geometry in which every two points of a topological plane are connected by a unique line (as in the Euclidean plane) but in which other axioms of Euclidean geometry may not apply.[4]
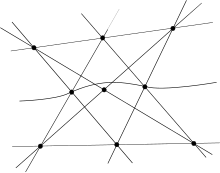
Notable arrangements of pseudolines which cannot be stretched include the arrangement of 9 pseudolines constructed by Friedrich Levi which violates the theorem of Pappus, and a 10 pseudoline arrangement constructed to violate Desargues's theorem.[5]
A common diagram used to represent an arrangement is the wiring diagram, a series of parallel lines with crossings between them drawn as an "X" in a simple crossing.[5] When drawn this way, they can be described with notation for either the order in which each line crosses the other, the state of the orders between each crossing (or allowed groups of crossing whose orders do not matter), or as a list of pairs, each pair being the labels of 2 lines which have crossed, ordered in a given direction (usually left to right). They draw similarities to braids, although without any need to keep track of which crosses atop the other, the crossings may be seen as elements of the Coxeter group.
References
[edit]- ^ Grünbaum (1972, p. 40); Agarwal & Sharir (2002).
- ^ This definition is from Grünbaum (1972, p. 40). For a comparison of alternative definitions of pseudolines, see Eppstein, Falmagne & Ovchinnikov (2007, pp. 238–239).
- ^ Shor (1991); Schaefer (2010, p. 334).
- ^ Goodman et al. (1994).
- ^ a b Felsner, Stefan; Goodman, Jacob E. (2017). "Pseudoline Arrangements" (PDF). Handbook of Discrete and Computational Geometry (3rd ed.). Chapman and Hall/CRC. ISBN 9781315119601.