Chirp compression
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
The chirp pulse compression process transforms a long duration frequency-coded pulse into a narrow pulse of greatly increased amplitude. It is a technique used in radar and sonar systems because it is a method whereby a narrow pulse with high peak power can be derived from a long duration pulse with low peak power. Furthermore, the process offers good range resolution because the half-power beam width of the compressed pulse is consistent with the system bandwidth.
The basics of the method for radar applications were developed in the late 1940s and early 1950s,[1][2][3] but it was not until 1960, following declassification of the subject matter, that a detailed article on the topic appeared the public domain.[4] Thereafter, the number of published articles grew quickly, as demonstrated by the comprehensive selection of papers to be found in a compilation by Barton.[5]
Briefly, the basic pulse compression properties can be related as follows. For a chirp waveform that sweeps over a frequency range F1 to F2 in a time period T, the nominal bandwidth of the pulse is B, where B = F2 – F1, and the pulse has a time-bandwidth product of T×B. Following pulse compression, a narrow pulse of duration τ is obtained, where τ ≈ 1/B, together with a peak voltage amplification of √T×B.
The chirp compression process – outline
[edit]In order to compress a chirp pulse of duration T seconds, which sweeps linearly in frequency from F1 Hz to F2 Hz, a device with the characteristics of a dispersive delay line is required. This provides most delay for the frequency F1, the first to be generated, but with a delay which reduces linearly with frequency, to be T second less at the end frequency F2. Such a delay characteristic ensures that all frequency components of the chirp pass through the device, to arrive at the detector at the same time instant and so augment one another, to produce a narrow high amplitude pulse, as shown in the figure:

An expression describing the required delay characteristic is
This has a phase component ψ(f), where
- , and the instantaneous delay td is given by
which has a linear slope with frequency, as required. In this expression, the delay characteristic has been normalized (for convenience), so as to give zero delay when the frequency f equals the carrier frequency f0. Consequently, when the instantaneous frequency is (f0 − B/2) or (f0 + B/2), the required delay is +T/2 or −T/2, respectively, so k = B/T.
The required dispersive characteristic may be obtained from a lumped element delay network,[6][7][8][9] a SAW device,[10][11][12][13][14] or by means of digital signal processing [15][16][17]
An overview of pulse compression concepts
[edit]Compression by matched filter
[edit]A chirp pulse, however generated, can be considered as the output of one of a pair of filters, which have dispersive characteristics. So, if the transmit filter has a group delay response which increases with frequency, then the receive filter will have one which decreases with frequency and vice versa.[6]
In principle, the transmitted pulses can be generated by applying impulses to the input of the dispersive transmit filter, with the resultant output chirp amplified as necessary for transmission. Alternatively, a voltage controlled oscillator may be used to generate the chirp signal.[6] To achieve maximum transmitted power (and so achieve maximum range) it is normal for a radar system to transmit chirp pulses at constant amplitude from a transmitter run in a near-limiting condition. The chirp signals reflected from targets are amplified in the receiver and then processed by the compression filter to give narrow pulses of high amplitude, as previously described.
In general, the compression process is a practical implementation of a matched filter system.[6][7] For the compression filter to be matched to the radiated chirp signal, its response is the complex conjugate of the time inverse of the transmit filter's impulse response. So, the output of this matched filter is given by the convolution of the signal h(t) with the conjugate impulse response h*(-t):
Alternately, if the frequency response of the coding filter is H(ω), then that of the matched filter is H*(ω), the spectrum of the compressed pulse is |H(ω)|2. The waveform of this spectrum is obtained from the inverse Fourier transform, i.e.
For the case of a linear chirp, with constant amplitude and time duration T, compression by the matched filter gives a waveform with the sinc characteristic, with duration 2T, as shown later. So, in addition to the main pulse, there are a large number of time sidelobes (or, more precisely, range sidelobes) present, the biggest of which are only 13.5 dB below the peak signal level.
In order to achieve a more desirable pulse characteristic (with lower sidelobes, for example), an alternative to the matched filter is often preferred. In this more general case, the compression filter has, say, impulse response g(t) and spectral response G(ω), so the equations for y(t) becomes:
and
When compared to the performance of the true matched filter, there will be some loss of processing gain, the main pulse lobe will be broader, and the total time duration of the compressed waveform will exceed 2T (usually).
The application of windowing to linear chirps
[edit]The sinc characteristic of a compressed pulse is a direct consequence of the spectrum of the linear chirp pulse having a rectangular profile. By modifying the spectrum to have a bell-shaped profile, by means of a weighting (or windowing, or apodization) function, lower level sidelobes are obtained.[4][18] When windowing is implemented, some signal attenuation occurs and there is a broadening of the main pulse, so both signal-to-noise ratio and range resolution are impaired by the process. Preferably, the transmitted and received pulses should be modified in equal measure, but when this is impractical, windowing in the compression filter alone is still beneficial.
Doppler tolerance of linear chirps
[edit]When the frequency sweep of a chirp is linear, the compression process is found to be very tolerant of Doppler frequency shifts on target returns, for a wide range of time-bandwidth products. It is only when T×B is very large (>2000, say) that loss of performance due to Doppler becomes an issue (with main-pulse broadening and increased sidelobe levels). In these situations a chirp with a hyperbolic frequency law can be used, as it has been shown to be fully tolerant to Doppler shifts.[19][20] Windowing techniques can still be applied to the compressed pulse spectra, to lower sidelobe levels, in a similar manner to linear chirps.[18]
Far-out sidelobes
[edit]There are different concerns when the time-bandwidth product is small. When T×B is less than about 75, the windowing process is not altogether successful, especially when it is applied only within the compressor. In such a situation, even though the close-in sidelobes are lowered by the anticipated amount, further away from the main lobe the sidelobes are found to increase in amplitude once more. These sidelobes tend to reach a maximum at locations ±T/2 on each side of the main lobe of the compressed pulse[21] and they are a consequence of the Fresnel ripples present on the frequency spectrum. This topic is discussed in more detail later.
There are techniques available that will reduce the amplitude of the spectral ripple (see chirp spectrum) and so reduce the amplitude of these far-out sidelobes, but they are not very effective when T×B. is small. In practice, the technique of "reciprocal ripple correction"[11][22][23] gives good results (where the spectrum of the compression filter is designed to have a ripple characteristic which is the inverse of that of the signal), but the method is less successful when signal returns contain large Doppler frequency shifts.
Non-linear chirps
[edit]An alternative method of obtaining a bell-shaped spectral shape in order to achieve lower sidelobes, is to sweep the frequency band in a non-linear manner. The required characteristic is obtained by having rapid changes in frequency near to the band edges, with a slower rate of change around band centre. This is a more efficient way of achieving the required spectral shape than by applying amplitude weighting to the spectrum of the linear chirp because no attenuation of signal power is necessary in order to achieve it.[8][24] In addition, the procedure gives far-out sidelobes that tend to be lower than those for the comparable linear sweep version. As the mathematics of non-linear chirps is more complicated than that of linear chirps, many early workers resorted to stationary phase methods to design them.[23][25]
The results obtained by using a non-linear sweep are particularly good when the time bandwidth product of the pulse is high (T×B >100). However, non-linear sweeps have to be used with caution when target returns are affected by Doppler frequency shifts. Even modest levels of Doppler can seriously degrade the profile of the main compressed pulse and raise sidelobe levels, as is shown later.
Generation of chirp waveforms – analogue methods
[edit]Many early dispersive filters were built using lumped element all-pass filter sections.,[8][9][23][26][27][28][29] but these proved hard to fabricate with any accuracy and it was difficult to achieve a satisfactory and repeatable performance. Consequently, the time sidelobe levels of the compressed pulses were high with these early systems, even after spectral weighting, with results no better than those achieved by phase coding or chip coding at that time.[30] Typically, sidelobe levels were in the range −20 to −25 dB [23] a poor result when compared to later achievements.
There were similar problems too, when a voltage controlled oscillator was used as a signal source. Matching the chirp characteristic from a VCO to a dispersive delay line proved difficult and, in addition, achieving adequate temperature compensation proved challenging.[7][31]
A major improvement in performance of chirp pulse generation and compression systems was achieved with the development of SAW filters.[11][32][33][34] These allowed much more precision in the synthesis of filter characteristics and consequently in the radar performance. The inherent temperature sensitivity of the quartz substrates was overcome by mounting both the transmit and receive filters in a common package, so providing thermal compensation. The increased precision offered by SAW technology, enabled time sidelobe levels approaching −30 dB to become achievable by radar systems. (In fact, the performance level now achievable was set more by limitations in the system hardware than in SAW shortcomings).
SAW technology still continues to be relevant to radar systems [12] and is particularly useful for systems using very wideband sweeps, where digital technology (see below) may not always be appropriate or may be difficult to implement.
Generation of chirp waveforms – digital methods
[edit]By the late 20th century, digital technology was able to offer a new approach to signal processing, with the availability of small high power computers together with fast D/A and A/D converters offering wide dynamic ranges. (see digital-to-analog converter and analog-to-digital converter).[16][17]
In a typical installation, data for the transmit pulses are stored in digital memory as a sequence of baseband I/Q samples (see quadrature phase), or as samples of a low IF waveform, and read out to a high speed D/A converters, as required. The analogue signal, so formed, is up-converted for transmission. On reception, returning signals are amplified and, typically, converted to a low IF or to baseband I/Q signals before being digitised by A/D converters. The compression of the chirps and additional signal processing is all performed by a digital computer, which has stored within it the chirp pulse data needed to carry out the compression process numerically.
Digital signal processing is conveniently carried out using FFT methods. If a chirp sequence is a(n) and that for the compression filter is b(n), then the compressed pulse sequence c(n) is given by
In practice, in a radar system, for example, it is not just a chirp pulse sequence that is to be compressed, but a long data sequence of returns from a given range spoke, within which the returning chirp pulse is located. For convenience, and to permit the use of FFTs of practical size, the data is divided into shorter lengths, which are compressed by repeated use the above equation. By applying the Overlap-save method, reconstruction of the full-duration compressed signal[35][36][37] is achieved. In this process, the transform sequence FFT{b(n)} has to be calculated only once, prior to storage in the computer for repeated use.
Pulse impairments due to system characteristics
[edit]There are many reasons why overall system performance is found to be disappointing; the presence of a Doppler shift on signal returns is a common cause for signal degradation, as was mentioned above. Some writers[38][39] favour using the ambiguity function[40] as a way of assessing the Doppler tolerance of chirps.
Others causes of signal impairment include amplitude ripple and slope across the passband, phase ripple across the passband, large band-edge phase shifts caused by band-limiting filters, phase modulation due to poorly regulated power supplies, all of which lead to higher sidelobe levels. Tolerances for these various parameters can be derived with the aid of paired echo theory.[23][41] Fortunately, with the aid of modern processing techniques and using a procedure similar to reciprocal ripple correction, or an optimization method with an adaptive filter it is possible to correct for many of these shortcomings.
Another type of waveform degradation is caused by eclipsing, where part of a returning chirp pulse is missing. As expected, this results in the loss of signal amplitude and a rise in sidelobe levels.[42]
A general closed form solution for chirp compression
[edit]The characteristic of a single linear chirp pulse, of unit amplitude, can be described by
where rect(z) is defined by rect(z) = 1 if |z| < 1/2 and rect(z) = 0 if |z| > 1/2
The phase response φ(t) is given by
and the instantaneous frequency fI is
So, during the T second duration of the pulse, the frequency changes in a linear fashion from f0 – kT/2 to f0 + kT/2. With the net frequency sweep defined as B, where B = (F1- F2), then k = B/T, as stated previously.
The spectrum of this waveform may be found from its transform
which is an integral which has been evaluated in chirp spectrum.
The spectrum of the compressed pulse can be found from
Where Y(f) is the spectrum of the compression filter.
The time domain waveform of the compressed pulse can be found as the inverse transform of . (This procedure has been described in a paper by Chin and Cook.[9][43])
Here it is more convenient to find from the convolution of the two time domain responses, i.e.
where the convolution of two arbitrary functions is defined by
However, in order to use this method, the impulse response of Y(f) is first needed. This is y(t), which is obtained from
A table of standard integrals[44] gives the following transform
Comparing the equations, they are equivalent if β = -j/k, so y(t) becomes
[Note: the same transform can also be found in Fourier transforms, no. 206, but with α replacing πβ]
With y(t) determined, the output sout(t) can be obtained from the convolution of s1(t) and y(t), i.e.
which can be simplified to
now as then
and finally
So, for a unit amplitude linear chirp, with a pulse duration T seconds and a frequency sweep B Hz (i.e. with a "time-bandwidth product" T.B), pulse compression gives a waveform with a magnitude given by
which has the form of the familiar sinc function. The collapsed pulse width τ, is of the order 1/B (with τ measured at the −4 dB points). Consequently, a pulse width reduction has occurred given by the ratio T/τ where
Also there is a signal amplification of
The main parameters are displayed in the figures below. The product T.B gives the compression ratio of the system and it equates, approximately, to the improvement in signal to noise ratio of the main lobe of the compressed pulse relative to that of the original chirp.

Properties of linear chirps
[edit]Pulse degradation caused by Fresnel ripples
[edit]In the closed form solution, just presented, the compressed waveform has the standard sinc function response, because a rectangular shape was assumed for the amplitude of the pulse spectrum. In practice, the spectrum of a linear chirp has a rectangular profile only when the time-bandwidth product of a pulse is large, i.e. when T×B exceeds 100, say. When the product is small, the spectral profile of the chirp pulse is seriously degraded by Fresnel ripples as shown in chirp spectrum and so is that of the matched filter. To investigate fully the consequences of these ripples it is advisable to consider each situation individually, either by evaluating convolution integrals, or more conveniently, by means of FFTs.
Some examples are shown below, for TB = 1000, 250, 100 and 25. They are dB plots which have all been normalised to have their pulse peaks set at 0 dB.


As can be seen, at high values of TB, the plots match the sinc characteristic closely, but at low values, significant differences can be seen. As already stated, these degradations in the waveforms, at low TB values, are because the spectral characteristics are no longer truly rectangular. In all cases, the close-in sidelobe levels are consistently high, at about −13.5 dB relative to the main lobe.
These range sidelobes are an unwelcome presence on the compressed pulse, because they will obscure signals of lower amplitude, which may also be present.
Reducing sidelobes by weighting functions
[edit]As the sinc-like characteristics of a compressed pulse are due to the near-rectangular profile of its spectrum, then by modifying that characteristic into a bell shape, for example, it is possible to reduce the sidelobe levels considerably. Previous work for antenna arrays and digital signal processing has already addressed this same problem. So, for example, in the case of antennas, the spatial sidelobes on the beam pattern are improved by applying a weighting function to the array elements,[45] and in the case of digital signal processing, window functions are used to reduce the amplitude of unwanted sidelobes[18] on the sampled functions.
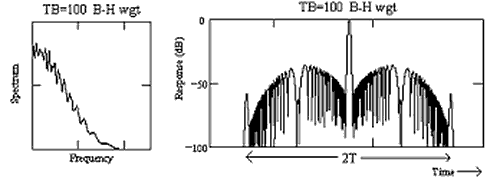
In an example of the process, the spectrum of a chirp pulse, with a time-bandwidth product of 250, is shown on the left, and is approximately rectangular in profile. Below this plot, also on the left, is shown the waveform after compression of the chirp by its matched filter and is similar to the sinc function, as expected. The top plot, on the right, is the spectrum after Hamming weighting. (This was achieved by applying a root-Hamming characteristic to both the chirp spectrum and to the compressor spectrum.) The compressed pulse corresponding to this spectrum, shown in the lower plots on the right, has much lower sidelobe levels.
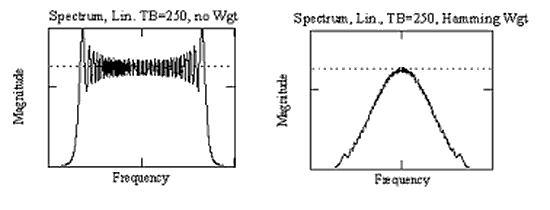

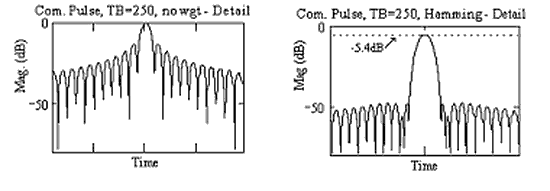
Although the sidelobe level has been much reduced, there are some undesirable consequences of the weighting process. Firstly, there is an overall loss of gain, with the peak amplitude of the main lobe reduced by about 5.4 dB and, secondly, the half-power beam width of the main lobe has increased by nearly 50%. In, say, a radar system, these effects would cause loss of range and reduced range resolution, respectively.
In general, the more the sidelobe levels are lowered, the broader the main lobe will become. However, the various windowing functions do perform differently from one other, with some giving main lobes which are unnecessarily broad for the sidelobe levels achieved. The most efficient function is the Dolph–Chebyshev window (see window functions) as this gives the narrowest pulse at a given sidelobe level.[18] A selection of the better performing windowing functions are shown in the graph of Beamwidth × Bandwidth as sidelobe level.
The lowest full line on the graph is for Dolph-Chebyshev weighting which, as already mentioned, sets the narrowest lobe possible for a given sidelobe level. So, from this plot, if a sidelobe level of −40 dB is desired, the graph shows that the smallest achievable half-power beamwidth × bandwidth is 1.2. Thus a chirp sweeping over a 20 MHz frequency band will have a compressed pulsewidth of 60 nanoseconds (at least).
As can be seen from the diagram, Taylor weighting is particularly efficient, and Hamming and the three and four term Blackman-Harris functions all give good results, too. Although the cosN functions perform badly, they have been included because they are amenable to mathematical manipulation and were studied in some detail in early work.[23][46]

Far-out sidelobes on compressed pulses
[edit]The example of a chirp with TB = 250 and Hamming weighting, given earlier, illustrates the benefits of weighting but is not representative of a normal situation because the results there were achieved by applying weighting equally to both the signal chirp and to its compressor. However, in a typical radar system the chirp pulse is usually transmitted by an amplifier operating in or near to compression, to maximise transmitter efficiency. In such a case, amplitude modulation of the chirp waveform or its spectrum is not possible, so the full window characteristic has to be incorporated into the compressor response. Unfortunately, this arrangement has undesirable consequences for the far-out sidelobes of the compressed pulse, especially when the time-bandwidth of the chirp is small.
Consider first the compressed pulse when TB = 250, which is shown in the left-hand figure below. For this result no weighting has been applied to the transmit pulse, but the full Hamming weighting has been applied in the compressor. As can be seen, the close-in sidelobe levels are consistent with the Hamming weighting (−42 dB), but further out, the sidelobe levels rise to a peak value of −45 dB at +/-T/2 each side of the main lobe. In the right-hand figure, where TB =25, the problems with the far-out sidelobes are much more serious. Here these sidelobes now rise to −25 dB at +/-T/2.

As a guide, the far-out sidelobe levels are given by
Slight variations on this equation are given in the literature,[47][48][49] but they only differ by a few dBs. Best results seem to be obtained when the window function is applied in the time domain to the compressor waveform (as amplitude modulation) rather than in the frequency domain to its spectrum.[50]
Reducing far-out sidelobes
[edit]As the far-out sidelobes are a consequence of the Fresnel ripple on the compressed pulse spectrum, any technique that reduces this ripple will also reduce the level of the sidelobes. In fact, there are several ways of achieving this reduction,[51] as shown below. Several of the methods are featured in chirp spectrum.
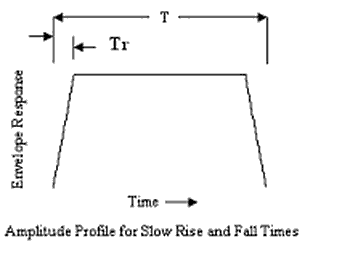
Introducing finite duration rise and fall times
[edit]A chirp with slow rise and fall times has reduced ripple on its spectrum (see chirp spectrum), so will result in lower time sidelobes on the compressed pulse. As an example, consider first the figure shows the compressed spectrum of a linear chirp, which has fast rise and fall times, with T×B = 100 and where Blackman-Harris weighting has been applied. The waveform corresponding to this spectrum has time sidelobes rising to about −40 dB, as predicted.

After linear rise and fall times are introduced, using the amplitude template shown, the ripple on the spectrum is much reduced and the time sidelobes are significantly lower, as shown.
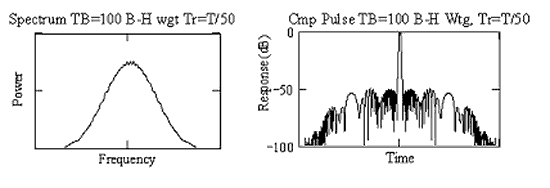
The procedure is most effective when both the signal chirp and the compressor chirp have modified rise-times, when sidelobe levels can be lowered by 15 – 20 dB. However, it is not always possible to apply amplitude modulation in the transmitter, so there is less improvement when only the compressor waveform is modified. Even so, a sidelobe reduction of about 6 dB can still be achieved.
The precise manner in which the rise and fall times are made less severe is not very critical, so the technique of adding cosine tapers to the compressed pulse spectrum (as with the Tukey[18] weighting function) gives a similar improvement – of several dBs.[21]
Improvements achieved by the method are tolerant of Doppler shifts.
Introducing 'tweaking' of the phase characteristic
[edit]An alternative form of waveform 'tweaking' is where frequency modulation distortion is applied to the chirps, instead of amplitude modulation.[23][52][53] The two types of distortion are functionally similar when the distortion levels are low. As with amplitude modulation, best results are obtained when both the expander and compressor waveforms are modified.
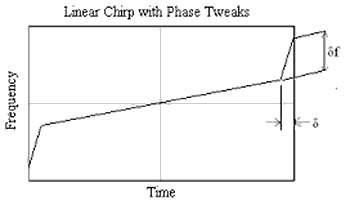
For best results Cook and Paolillo recommend δf = 0.75×B and δ = 1/B.
As an example, a pulse considered earlier, with T×B = 100 and Blackman–Harris weighting, is modified with phase tweaking and the results are shown. There is reduced ripple on the compressed pulse spectrum and the far-out sidelobes have been reduced.

The improvements are maintained even when Doppler frequency shifts are present on the signals. In a more recent paper [54] slightly different parameters have been suggested, namely δ = 0.86/B and δf = 0.73×B.
Also, Kowatsch and Stocker[21] has reported improved results by applying a cubic distortion function (whereas Cook and Paolillo's technique may be termed "square-law modulation distortion"). This new characteristic is also tolerant of Doppler frequency shifts.
Reciprocal ripple correction
[edit]The spectral response of the matched filter has a magnitude which is the mirror image of that of the expanded pulse, when a chirp spectrum has symmetry about its centre frequency, so the Fresnell ripples on the spectrum are augmented by the compression process. What is needed to reduce the ripples is a compression filter whose spectrum has the inverse (reciprocal) ripple to that of the expander.[23] As this will no longer be a matched filter, there will be increased mismatch loss. In his early work[6][9][23] Cook did not recommend attempting such a procedure because the filters needed were considered too difficult to make. However, with the advent of SAW technology it became possible to achieve the required characteristics.[11][12][22][33] More recently, digital techniques with mathematically derived look-up tables have provided a convenient way of introducing reciprocal ripple correction.[16]
The spectrum of the compressed pulse is the product of the spectra of the expander and compressor filters, as given earlier. Now, instead of C(ω), a new output spectrum C'(ω) is defined, which has no Fresnell ripples but which defines a desired sidelobe structure (such as that defined by a Hamming window). The compression filter that will achieve this requirement is determined by the equation
where H(ω) is the spectrum of the signal, C'(ω) is the target spectrum for the compressed pulse and has the low sidelobes of the chosen weighting function and K(ω) is the spectrum of the compression filter which has the reciprocal ripple properties. Close-in sidelobes are automatically dealt with in the process.
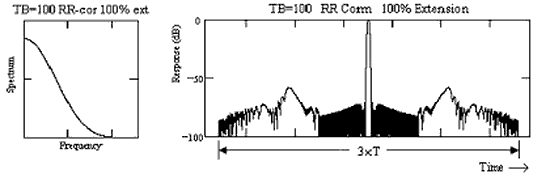
As an example of the procedure consider a linear chirp with T×B =100. The left-hand figures shows (one half of) the spectrum of the chirp, and the right-hand figure shows the waveform after compression. As expected, close-in sidelobes start at −13.5 dB.

In the next figure, Blackman-Harris weighting has been applied to the compressed pulse spectrum. Although the close-in sidelobes have been reduced, the far-out sidelobes remain high with a predicted level of, approximately −20×log10(100) = -40 dB, as predicted for a time-bandwidth product of 100. With lower time-bandwidth products, these sidelobes will be even higher.
Next, a compression filter that provides reciprocal-ripple correction has been used. As can be seen, a ripple-free spectrum has been achieved resulting in a waveform that is free from high level far-out sidelobes.

However, this procedure has a problem. Although the process has found a compressor spectrum that leads to low sidelobes on the compressed pulse, no account was taken of the waveform this spectrum might have. When an inverse Fourier transform is carried out on this spectrum, in order to determine the characteristics of its waveform, it is found that the waveform is of extremely long duration, typically exceeding 10T. Even assuming the waveform is no longer than 10T, it means that the total time needed to process one chirp will be at least 11T, in total, a length of time unacceptable in most circumstances.
In order to achieve a practical solution Judd[22] proposed that the total length of the compression pulse be truncated to 2T, whereas Butler[11] suggested 1.6T and 1.3T. Extensions as low as 10% have also been used[55]
Unfortunately, when the new compressor waveform is truncated, then far-out sidelobes reappear once more. The next figures shows what happens to the compressed pulse when the compressor is set at 2T duration and then at 1.1T duration. New far-out sidelobes have appeared with amplitudes that make them clearly visible. These sidelobes are often referred to as "gating sidelobes".[54] They can be irritatingly high but, fortunately, even if the compressor is set have just 10% extension, the sidelobes are still at a level than that achieved without correction.

Any Doppler frequency shift on the received signals will degrade the ripple cancelation process[11][21] and this is discussed in more detail next.
Doppler tolerance of linear chirps
[edit]Whenever the radial distance between a moving target and the radar changes with time, the reflected chirp returns will exhibit a frequency shift (Doppler shift). After compression, the resulting pulses will show some loss in amplitude, a time (range) shift and degradation in sidelobe performance.[23]
In a typical radar system, the Doppler frequency is a small fraction of the swept frequency range (i.e. the system bandwidth) of the chirp, so the range errors due to Doppler are found to be minor. For example, for fd<<B/2, the time shift is given by.[56]
and where fd is the Doppler frequency, B is the frequency sweep of the chirp, T is the duration of the chirp, fm is the mid (centre) frequency of the chirp, Vr is the radial velocity of the target and c is the velocity of light (= 3×108 m/s).
Consider as an example, a chirp centered on 10 GHz, with pulse duration of 10μs and a bandwidth of 10 MHz. For a target with an approach velocity of Mach1 (≈ 300 m/s), the Doppler shift will be about 20 kHz and the time shift of the pulse will be about 20ns. This is roughly one fifth of the compressed pulse width and corresponds to a range error of about 7.5 metres. In addition there is a tiny loss in signal amplitude (approximately 0.02 dB).
Linear chirps with a time-bandwidth product of less than 2000, say, are found to be very tolerant of Doppler frequency shifts, so main pulse width and the time sidelobe levels show little change for Doppler frequencies up to several percent of system bandwidth. In addition, linear chirps which use phase pre-distortion to lower sidelobe levels, as described in an earlier section, are found to be tolerant of Doppler.[21]
For very large Doppler values (up to 10% of system bandwidth), time sidelobes are found to increase. In these cases Doppler tolerance can be improved by introducing small frequency extensions onto the spectra of the compressed pulses.[47] The penalty for doing this is, either, an increase in main lobe width, or an increase in bandwidth requirements.
Only when chirp time-bandwidth products are very high, say well over 2000, is it necessary consider a sweep-frequency law other than linear, to cope with Doppler frequency shifts. A Doppler tolerant characteristic is the linear-period (i.e. hyperbolic) modulation of the chirp, and this has been discussed by several authors,[19][20] as was mentioned earlier
If reciprocal-ripple correction has been implemented in order to lower the time-sidelobe levels, then the benefits of the technique diminish as the Doppler frequency is increased. This is because the inverse ripples on the signal spectrum are shifted along in frequency and the reciprocal ripple of the compressor no longer matches those ripples. It is not possible to determine a precise Doppler frequency at which r-r fails because the Fresnell ripples on chirp spectra do not have a single dominant component. However, as a rough guide, r-r correction ceases to be of benefit when
Non-linear chirps
[edit]To ensure that a compressed pulse has low time sidelobes, its spectrum should be approximately bell-shaped. With linear chirp pulses this can be achieved by applying a window function either in the time domain or in the frequency domain, i.e. by amplitude modulating the chirp waveforms or by applying weighting to the compressed pulse spectra. In either case there is a mismatch loss of 1.5 dB, or more.
An alternative way to obtain the required spectral shape is to use a non-linear frequency sweep in the chirp. In this case, to achieve the required spectral shape, the frequency sweep changes very rapidly at band edges and more slowly around band centre. Consider, as an example, the frequency versus time plot that achieves the Blackman-Harris windowing profile. When T×B =100, the spectrum of the compressed pulse and the compressed waveform are as shown.
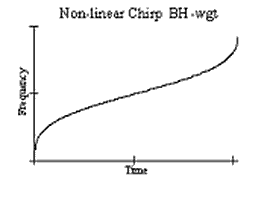

The required non-linear characteristic can be derived using the method of stationary phase.[24][57] As this technique does not take account of the Fresnel ripples, these have to be dealt with in additional ways, as was the case with linear chirps.
In order to achieve the required spectral shape for low time sidelobes, linear chirps require amplitude weighting and consequently incur a mismatch loss. Non-linear chirps, however, have the advantage that by achieving the spectral shaping directly, close-in sidelobe levels can be made low with negligible mismatch loss (typically less than 0.1 dB). Another benefit is that the far out sidelobes, due to Fresnel ripples on the spectrum, tend to be lower than for a linear chirp with the same T×B product (4 to 5 dB lower with large T×B).
However, for chirps where the T×B product is low, the far-out sidelobe levels of the compressed pulse can still be disappointingly high, because of high amplitude Fresnel ripples on the spectrum. As with linear chirps, results can be improved by means of reciprocal ripple correction but, as previously, truncation of the compression waveform results in the appearance of gating sidelobes.
An example of reciprocal ripple and truncation is shown below. The left hand figure shows the spectrum of a non-linear chirp, with a time bandwidth product of 40, aiming to have a Blackman-Harris profile. The right-hand figure shows the compressed pulse for this spectrum,

The next figures shows the spectrum after r-r compensation, but with truncation of the compression waveform to 1.1T, and the final compressed waveform.

Doppler tolerance of non-linear chirps
[edit]A major disadvantage of non-linear chirps is their sensitivity to Doppler frequency shifts. Even modest values of Doppler will result in broadening of the main pulse, raising of the sidelobe levels, increase in mismatch loss and the appearance of new spurious sidelobes.
An example of a non-linear chirp pulse and the effects of Doppler are shown. The non-linear characteristic is chosen to achieve −50 dB sidelobes using Taylor weighting. The first figure shows the compressed pulse for a non-linear chirp, with bandwidth 10 MHz, pulse duration 10usec, so T×B = 100, and with no Doppler shift. The next two figures shows the pulse degradation cause by 10 kHz and 100 kHz Doppler, respectively. In addition to the waveform degradation, the mismatch loss increases to 0.5 dB. The final figure shows the effect of 100 kHz Doppler on a linear chirp which has had amplitude weighting applied to give the same spectral shape as that of the non-linear chirp. The greater tolerance to Doppler is clearly seen.


Cook,[23] using paired-echo distortion methods,[41] estimated that in order to keep sidelobe levels below −30 dB, the maximum allowed Doppler frequency is given by
so, for a 10μs pulse, the maximum Doppler frequency that can be tolerated is 6 kHz. However, more recent work suggests that this is unduly pessimistic.[33] In addition, as the new sidelobes, when at a low level, are very narrow. Consequently, it may be possible to ignore them initially, as they may not be resolvable by the receiver's D to A.
Using a combination of non-linear and linear characteristics to improve Doppler tolerance
[edit]A way of reducing the susceptibility of non-linear chirps to Doppler is to use a "hybrid" scheme, where part of the spectral shaping is achieved by a non-linear sweep, but with additional spectral shaping achieved by amplitude weighting.[11][12] Such a scheme will have greater mismatch loss than a true non-linear scheme, so the advantage of greater Doppler tolerance has to be weighed against the disadvantage of the increased mismatch loss.
In the two examples below, the chirps have a non-linear sweep characteristic which gives a spectrum with Taylor weighting which, used alone, will achieve a sidelobe level of −20 dB on its compressed pulses. To achieve lower level sidelobes, this spectral shape is augmented by amplitude weighting so that the final target sidelobe level for the compressed pulses is −50 dB. Comparing the results for Doppler shifts of 10 kHz and 100 kHz with those shown earlier it is seen that the new spurious sidelobes, caused by the Doppler, are seen to be 6 dB lower than before. However, the mismatch loss has increased from 0.1 dB to 0.6 dB, but this is still better than the 1.6 dB figure for linear chirps.

Signal-to-noise ratio improvements by pulse compression
[edit]The amplitude of random noise is not changed by the compression process, so the signal to noise ratios of received chirp signals are increased in the process. In the case of a high power search radars, this extends the range performance of the system, while for stealth systems the property will permit lower transmitter powers to be used.
As an illustration, a possible received noise sequence is shown, which contains a low amplitude chirp signal obscured within it. After processing by the compressor, the compressed pulse is clearly visible above the noise floor.


When pulse compression is carried out in digital signal processing, after the incoming signals are digitised by A/D converters, it is important that level of the noise floor is correctly set. The noise floor at the A/D must be high enough to ensure that the noise is adequately characterised. If the noise level is too low, Nyquist will not be satisfied, and any embedded chirp will not be recovered correctly. On the other hand, setting the noise level unnecessarily high will reduce the dynamic range capability of the system.
For systems using digital processing, it is important to carry out the chirp compression in the digital domain, after the A/D converters. If the compression process is carried out in the analogue domain before digitization (by a SAW filter, for example), the resulting high-amplitude pulses will place excessive demands on the dynamic range of the A/D converters.[17]
Pre-correction of system characteristics
[edit]The transmitter and receiver subsystems of a radar are not distortion free. In consequence system performance is often less than optimum. In particular, the time sidelobe levels of the compressed pulses are found to be disappointingly high.
Some of the characteristics which degrade performance are:
- Gain slope, or non-linear phase slope, across the system passband.
- Amplitude and phase ripple across the passband (which may be caused by mismatches on interconnecting cables[58] as well as by imperfections in amplifiers).
Delay modulation by the transmitter (if power supply regulation is poor).
In addition, filters employed in the frequency conversion processes of the transmitter and receiver all contribute to gain and phase variations across the system passband, especially near to band edges. In particular, major contributors to overall non-linear phase characteristics are the low-pass filters preceding the A/D converters, which are usually sharp-cut filters chosen to ensure maximum bandwidth while minimizing aliased noise. The transient response characteristics of these filters contribute another (unwanted) source of time sidelobes.
Fortunately it is possible to compensate for several system properties, provided they are stable and can be characterized adequately when a system is first assembled. This is not difficult to implement in radars using digital look-up tables, since these tables can be easily amended to include compensation data. Phase pre-corrections can be included in the expander tables and phase and amplitude corrections can be included in the compressor tables, as required.
So, for example, the earlier equation, defining the compressor characteristic to minimize spectral ripple, could be expanded to include additional terms to correct for known amplitude and phase impairments, thus:
where, as before, H(ω) is the initial chirp spectrum and C'(ω) is the target spectrum, such as a Taylor window, but now additional terms have been included, namely, Φ((ω) ) and A(ω) which are the phase and amplitude characteristics that require compensation.
A compressor chirp waveform that includes phase correction data will have additional ripple components present at each end of the waveform (pre-shoots and after-shoots). Any truncation procedure should not remove these new features.
In addition, it is easy to time shift the compressed pulses by ±t0, by multiplying the compressor spectrum by the unity amplitude vector, i.e.
- .
Time shift can be useful to position the main lobes of compressed pulses at a standard location, regardless of chirp pulse length. However, care has to be taken with the overlap and save or overlap and discard algorithm, should time shift be used, to ensure only valid waveform sequences are retained.
There has been a growth in interest in adaptive filters for pulse compression, made possible by the availability of small fast computers, and some relevant articles are mentioned in the next section. These techniques will also compensate for hardware deficiencies, as part of their optimization procedure[59]
More recent work on chirp compression techniques – some examples
[edit]The growth in digital processing and methods had a significant influence in the field of chirp pulse compression. An introduction to these techniques is provided in a chapter of the Radar Handbook (3rd ed.), edited by Skolnik.[17]
The main aims of most investigations into pulse compression has been to obtain narrow main lobes, with low sidelobe levels, a tolerance to Doppler frequency shifts and to incur low system losses. The availability of computers has led to a growth in numerical processing and much interest in adaptive networks and optimization methods, to achieve these aims. For example, see the comparison of the various techniques made by Damtie and Lehtinen[60] and, also, various articles by Blunt and Gerlach on these topics.[61][62][63][64] A number of other contributors in the field has included Zrnic et al.[65] Li et al.[49] and Scholnik.[59]
A number of other works, with a variety of approaches to pulse compression, are listed below:
- New methods of generating non linear chirp waveforms and of improving their Doppler tolerance has been investigated by Doerry[66][67]
- Further studies of Hyperbolic chirps have been carried out by Kiss,[68] Readhead,[69] Nagajyothi and Rajarajeswari[70] and Yang and Sarkar.[71]
- Convolution windows have been investigated by Sahoo and Panda who show that they can result in very low sidelobes yet be Doppler tolerant, but may suffer from some pulse broadening.[72] Wen and his co-workers have also discussed convolution windows.[73][74]
- Some new window functions have been proposed by Samad[75] and Sinha and Ferreira,[76] which claim improved performance over the familiar functions.
- Several techniques to lower the sidelobe levels of the compressed pulses for non-linear FM chirps are compared by Varshney and Thomas.[77]
- In a paper by Vizitui,[78] sidelobe reduction is considered where phase pre-distortion is applied to non-linear FM chirps, rather than to linear chirps. Lower sidelobes and some improvement in Doppler tolerance is claimed.
There have been extensive investigations of phase modulation for pulse compression schemes, such as biphase (binary phase-shift keying) and polyphase coding methods, but this work is not considered here.
See also
[edit]References
[edit]- ^ Dicke R. H.,"Object Detection System", U.S. Patent 2,624,876, submitted Sept. 1945
- ^ Darlington S.,"Pulse Transmission", U.S. Patent 2,678,997, submitted Sept. 1945
- ^ Sproule D. O. and Hughes A. J., "Improvements in and Relating to System Operation by Means of Wave Trains", U.K. Patent 604,429, submitted June 1945
- ^ a b Klauder J. R., Price A. C., Darlington S. and Albersheim W. J., "The Theory and Design of Chirp Radars", BSTJ Vol. 39, July 1960, pp. 745–808
- ^ Barton D. K. (ed), "Radars, Volume 3, Pulse Compression", Artech House 1975, 1978
- ^ a b c d e Bernfeld M., Cook C. E., Paolillo J., and Palmieri C. A., "Matched Filtering, Pulse Compression and Waveform Design", Microwave Journal, Oct 1964 – Jan 1965, (34 pp.)
- ^ a b c Farnett E. C. & Stevens G. H., "Pulse Compression Radar", Chapter 10 of "Radar Handbook, 2nd Ed.", ed Skolnik M., McGraw Hill 1990
- ^ a b c Millett R. E., "A Matched-Filter Pulse-Compression System Using a Non-linear F.M. Waveform", IEEE Trans. Aerospace and Electronic Systems, Vol. AES-6, No. 1, Jan 1970, pp. 73–78
- ^ a b c d Cook C. E., "Pulse Compression – Key to More Efficient Radar Transmission", Proc. IRE, Vol.48, March 1960, pp. 310–316
- ^ Jones W. S., Kempf R. A. and Hartman C. S., "Practical Surface Wave Chirp Filters for Modern Radar Systems", Microwave Journal, May 1972, pp. 43–50
- ^ a b c d e f g Butler M. B. "Radar applications of s.a.w. dispersive filters", Proc IEE, Vol.27, Pt. F, April 1980, pp.118–124
- ^ a b c d Arthur J. W., Modern SAW-based pulse compression systems for radar applications. Part 1: SAW matched filters, Part 2: Practical systems", Electronics & Communication Engineering Journal, Dec 1995, pp. 236–246, and April 1996, pp. 57–79
- ^ Andersen Laboratories, "Handbook of Acoustic Signal Processing, Vols. 2 & 3, SAW Filters and Pulse Expansion/Compression IF Subsystems for Radar"
- ^ MESL Microwave, "SAW Pulse Compression" (technical brochure), http://www.meslmicrowave/saw-pulse-compression/technical-notes/[dead link]
- ^ Halpern H. M. and Perry R. P., "Digital Matched Filters Using Fast Fourier Transforms", IEEE EASTCON '71 Record, pp. 222–230
- ^ a b c Arthur J. W., "Digital Waveform Generation for SAW Compression Systems", Tech. Note, Racal MESL, Newbridge, Midlothian
- ^ a b c d Alter J. J. and Coleman J. O., "Digital Signal Processing", Chapter 25 of "Radar Handbook, 3rd edition", Skolnik M. I. (ed.), McGraw Hill 2008
- ^ a b c d e Harris F. J., "On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform", Proc. IEEE, Vol.66, Jan 1978, pp.174–204
- ^ a b Thor R. C., "A large Time-Bandwidth Product Pulse Compression Technique", Trans IRE MIL-6, No. 2, April 1962, pp. 169–173
- ^ a b Kroszczynski J. J., "Pulse Compression by Means of Linear-Period Modulation", Proc. IEEE, Vol. 57, No. 7, July 1969, pp. 1260–1266
- ^ a b c d e Kowatsch M. and Stocker H. R., "Effect of Fresnel ripples on sidelobe suppression in low time-bandwidth product linear FM", IEE Proc. Vol, 129, Pf.F, No. 1, Feb 1982, pp. 41–44
- ^ a b c Judd G. W., "Technique for Realising Low Time Sidelobe Levels in Small Compression Ratio Chirp Waveforms", Proc. IEEE Ultrasonics Symposium, 1973, pp.478–483
- ^ a b c d e f g h i j k Cook C. E. and Bernfeld M., "Radar Signals, An Introduction to Theory and Application"; Academic Press 1967, 1987; Artech House 1993
- ^ a b Key E. L., Fowle E. N., Haggarty R. D., "A Method of Designing Signals of Large Time-Bandwidth Product", Proc. IRE Int. Conf. Rec. Pt.4, Mar 1961, pp. 146–154
- ^ Fowle E. N., "The design of FM pulse-compression signals", IEEE Trans. IT-10, 1964, pp. 61–67
- ^ Abel J. S. and Smith J. O., "Robust Design of Very High Order All-pass Dispersion Filters", Proc. 9th Int. Conf. on Digital Audio Effects (DAFx-06), Montreal Canada, Sept 2006
- ^ Farnett E. C. and Stevens G. H., "Pulse Compression Radar", Chapter 10 of "Radar Handbook 2nd Ed.", ed Skolnik M., McGraw Hill 1990
- ^ Brandon P. S., "The Design Methods for Lumped-Constant Dispersive Networks Suitable for Pulse Compression Radar", Marconi Review, Vol. 28, No. 159, 4th qtr. 1965, pp. 225–253
- ^ Steward K. W. F., "A Practical Dispersive Network System", Marconi Review, Vol. 28, No. 159, 4th qtr. 1965, pp. 254–272
- ^ Barton D. K. Modern Radar System Analysis", Artech House 1988, pp.220–231
- ^ Mortley W. S., "A Pulse Compression System for Radar, Part 2: Practical Realization", Industrial Electronics, Nov. 1965, pp. 518–520
- ^ Jones W. S., Kempf R. A. and Hartman C. S., "Practical Surface Wave Chirp Filters for Modern Radar Systems", Microwave Journal, May 1972
- ^ a b c Newton C. O., "Nonlinear Chirp Radar Signal Waveforms for Surface Acoustic Wave Pulse Compression Filters", Wave Electronics, No. 1, 1974/6, pp. 387–401
- ^ Arthur J. W., "Modern SAW-based pulse compression systems for radar applications. Part 1: SAW matched filters", Electronics & Communication Engineering Journal, Dec. 1995, pp. 236–246
- ^ Oppenheim A. V. and Schaffer R. W., "Digital Signal Processing", Prentice Hall 1975, pp.113–115
- ^ Harris F. J., "Convolution, Correlation and Narrowband Filtering with the Fast Fourier Transform", San Diago State Univ., CA,(sponsored paper Int. Def. Elec. Assoc.)
- ^ Smith S. W., "Digital Signal Processing", Newnes 2003, p. 311
- ^ Rihaczek A. W., "Principles of High-Resolution Radar", McGraw Hill 1969, Artech House 1996
- ^ Mahafza B. R. "Radar system Analysis and Design using MATLAB", Chapman & Hall/CRC, 2000
- ^ Woodward P. M., "Probability and information theory with applications to radar", Pergamon Press 1953, 1964
- ^ a b Wheeler H. A., "The Interpretation of Amplitude and Phase Distortion in Terms of Paired Echoes", Proc. IRE, June 1939, pp. 359–385
- ^ Billam E. R., "Eclipsing Effects with High Duty Factor Waveforms in Long Range Radar", IEEE International Radar Conference 1985
- ^ Chin J. E. and Cook C. E., "The Mathematics of Pulse compression", Sperry Engineering Review, Vol. 12, Oct. 1959, pp. 11–16
- ^ Campbell G. A. and Foster R. M. "Fourier Integrals for Practical Applications", van Nostrand 1948, number 708.0. Also in BSTJ, Oct. 1928, pp. 639–707
- ^ Taylor T. T., "Design of Line-Source Antennas for narrow Beamwidth and Low Side Lobes", IRE Trans., Antennas and Prop., Jan 1955, pp. 169–173
- ^ Cook C. E., Bernfeld M. and Palmieri C. A., "Matched Filtering, Pulse Compression and Waveform Design", Microwave Journal Jan 1965
- ^ a b Kowatsch M., Stocker H. R., Seifert F. J. and Lafferl J., "Time Sidelobe Performance of Low Time-Bandwidth Product Linear FM Pulse Compression System", IEEE Trans. on Sonics and ultrasonics, Vol SU-28, No. 4, July 1981, pp. 285–288
- ^ Vincent N., "Rain Radar (Final Presentation) – Introduction", Alcatel Espace, Nordwijk, Nov. 1995
- ^ a b Li L., Coon M. and McLinden M., "Radar Range Sidelobe Reduction Using Adaptive Pulse Compression Techniques", NASA Tech Brief GSC-16458-1, October 2013
- ^ McCue J. J. G., "A Note on the Hamming Weighting of Linear-FM Pulses", Proc. IEEE, Vol. 67, No. 11, Nov 1949
- ^ Cook C. E. and Paolillo J., "A Pulse Compression Predistortion Function for Efficient Sidelobe Reduction in a High-Power Radar", Proc. IEEE, Vol. 52, April 1964, pp. 377–389
- ^ Cook C. E. And Paolillo J., "A Pulse Compression Predistortion Function for Efficient Sidelobe Reduction in a High Power Radar", Proc. IEEE, Vol. 52, April 1964, pp. 377–389
- ^ Vincent N., "Rain Radar (Final Presentation) – Selected Concept and overall design", Alcatel Espace, Nordwijk Nov. 1995
- ^ a b Solal M., "High Performance SAW Delay Lines for Low Time Bandwidth Using Periodically Sampled Transducers", IEEE Ultrasonics Symposium (Chicago), Nov. 1988
- ^ Racal-MESL Brochure, "Pulse Compression", Technical Brochure TP510, 1990
- ^ Terman F. E., "Electronic and Radio Engineering, 4th Edition", McGraw Hill 1955, p.1033
- ^ Fowle E. N., "The design of FM pulse-compression signals", IEEE Trans. IT-10, 1964, pp. 61–64
- ^ Reed J., "Long Line Effect in Pulse Compression Radar", Microwave Journal, September 1961, pp. 99–100
- ^ a b Scholnik D., "Optimal Filters for Range-Time Sidelobe Suppression" Naval Research Lab., Washington, DC
- ^ Damtie B. and Lehtinen M. S., "Comparison of the performance of different radar pulse compression techniques in an incoherent scatter radar measurement", Ann. Geophys., Vol. 27, 2009, pp. 797–806
- ^ Blunt S. D. and Gerlach G., "A Novel Pulse Compression Scheme Based on Minimum Mean-Square Error Reiteration", IEEE RADAR 2003, Australia 2003, pp. 349–353
- ^ Blunt S. D. and Gerlach G., "Adaptive Pulse Compression via MMSE Estimation", IEEE Trans. Aerospace and Electronic Systems, Vol. 42, No. 2, April 2006, pp. 572–583
- ^ Blunt S. D. and Gerlach G.,"Adaptive Radar Pulse Compression", NRL Review 2005, Simulation Computing and Modelling, 2005, pp. 215–217
- ^ Blunt S. D., Smith K. J. and Gerlach G., "Doppler-Compensated Adaptive Pulse Compression", IEEE Trans., 2006, pp. 114–119
- ^ Zrnic B., Zejak A., Petrovic A. and Simic I., "Range sidelobe suppression for pulse compression radars utilizing modified RLS algorithm", IEEE 5th Int. Symp. Spread Spectrum Techniques and Applications, 1998, pp. 1008–1011
- ^ Doerry A. W., "Generating Nonlinear FM Chirp Waveforms for Radar", Sandia Report SAND2006-5856, Sandia National Laboratories, Sept. 2006, p. 34
- ^ Doerry A. W., "Generating Nonlinear FM Chirp Radar Signals by Multiple Integrations", U.S. Patent 7,880,672 B1, Feb 2011, p. 11
- ^ Kiss C. J., "Hyperbolic-FM (Chype)", US Army Missile Res., Dev. & Eng. Lab., Alabama 35809, Report No. RE-73-32, 1972
- ^ Readhead M., "Calculations of the Sound Scattering of Hyperbolic Frequency Modulated Chirp Pulses from Sonar Targets", www.dsto.defence.gov.au/corporate/reports/DSTO-RR-0351.pdf Feb 2010, p. 43
- ^ Nagajyothi A. and Rajarajeswari K., "Delay-Doppler Performance of Hyperbolic Frequency Modulation Waveforms", Intl. Jour. Electrical, Electronics and Data Communications, ISSN 2320-2084, vol. 1, Iss. 9, Nov 2013
- ^ Yang J. and Sarkar T. K., "Acceleration-invariance of hyperbolic frequency modulated pulse compression"
- ^ Sahoo A. K. and Panda G., "Doppler Tolerant Convolution Windows for Radar Pulse Compression", Int. Jour.Electronics and Communication Engineering, ISSN 0974-2166, Vol. 4, No. 1, "011, pp.145–152
- ^ Wen H., Teng Z. S., Guo S. Y., Wang J. X., Yang B. M., Wang Y. and Chen T., "Hanning self-convolution window and its application to harmonic analysis", Science in China, Series E: Technological Sciences 2009, p. 10
- ^ Wen H., Teng Z. and Gao S., "Triangular Self-Convolution Window with Desirable Sidelobe Behaviours for Harmonic Analysis of Power System", IEEE Trans. Instr. and Measurement, Vol59, No. 3, March 2010, p. 10
- ^ Samad M. A., "A Novel Window Function Yielding Suppressed Mainlobe Width and Minimum Sidelobe Peak", Int. Jour. Computer Science, Engineering and Information Technology (IJCSEIT), Vol. 2, No. 2, April 2012
- ^ Sinha D. and Ferreira A. J. S., "A New Class of smooth Power Complementary Windows and their Application to Audio Signal Processing", Audio Eng. Soc. Conv. Paper, 119th Convention, Oct 2005, www.atc-labs.com/technology/misc/windows/docs/aes119_218_ds.pdf
- ^ Varshney L. R. and Thomas D., "Sidelobe Reduction for Matched Filter Range Processing", IEEE Radar Conference 2003, p. 7
- ^ Vizitui J. C., "Some Aspects of Sidelobe reduction in Pulse Compression Theory, using NLFM Signal Processing", Progress in Electronics Research, C, Vol. 47, 2014, pp. 119–129

![{\displaystyle Y(f)=\exp[j\pi (f-f_{0})^{2}/k]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67609be8288313b48b19c61042bfc3441b4cdb01)






![{\displaystyle c_{1}(n)=IFFT[FFT\left\{a(n)\right\}^{*}FFT\left\{b(n)\right\}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b2ef17414d4a83c9e24bb06d1d09b278816e1e7)



![{\displaystyle S_{1}(f)=\int _{-\infty }^{\infty }s_{1}(t).e^{-j2\pi .ft}.dt=\int _{-{\frac {T}{2}}}^{\frac {T}{2}}e^{j2\pi .[(f_{0}-f)t+{\frac {kt^{2}}{2}}]}.dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5b0951c42af49adeca924ec07670e825bd5eaa1)













![{\displaystyle \int _{-T/2}^{T/2}e^{j2\pi .kt\tau }.d\tau ={\frac {1}{j2\pi kt}}.{\Bigl [}e^{j2\pi .kt\tau }{\Bigr ]}_{\text{-T/2}}^{\text{T/2}}={\frac {1}{j2\pi kt}}[e^{j2\pi kT/2}-e^{-j2\pi kT/2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68a660ffa99ca69eb3e8606798084f6e17b6b0d0)

![{\displaystyle s_{\text{out}}(t)={\frac {1}{\pi kt}}\cdot {\sqrt {\frac {jB}{T}}}\cdot \sin(\pi Bt).\exp[j2\pi (f_{0}t-kt^{2}/2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c899bc13a4c554e2230474344a124979047a3901)
![{\displaystyle ={\sqrt {T.B}}\cdot {\frac {\sin(\pi Bt)}{\pi Bt}}\cdot {\sqrt {j}}\cdot \exp[j2\pi (f_{0}t-kt^{2}/2)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54a478bbb6c39a0472c3cc62bd6f210818836257)









