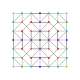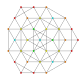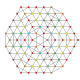| #
|
Coxeter-Dynkin diagram
Schläfli symbol
Johnson name
|
Ak orthogonal projection graphs
|
A7
[8]
|
A6
[7]
|
A5
[6]
|
A4
[5]
|
A3
[4]
|
A2
[3]
|
| 1
|
            
t0{3,3,3,3,3,3}
7-simplex
|

|

|

|

|

|

|
| 2
|
            
t1{3,3,3,3,3,3}
Rectified 7-simplex
|

|

|

|

|

|

|
| 3
|
            
t2{3,3,3,3,3,3}
Birectified 7-simplex
|

|

|

|

|

|

|
| 4
|
            
t3{3,3,3,3,3,3}
Trirectified 7-simplex
|

|

|

|

|

|

|
| 5
|
            
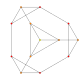
t0,1{3,3,3,3,3,3}
Truncated 7-simplex
|

|

|

|

|

|
|
| 6
|
            
t0,2{3,3,3,3,3,3}
Cantellated 7-simplex
|

|

|

|

|

|

|
| 7
|
            
t1,2{3,3,3,3,3,3}
Bitruncated 7-simplex
|

|

|

|

|

|

|
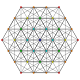
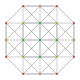
| 8
|
            
t0,3{3,3,3,3,3,3}
Runcinated 7-simplex
|

|

|
|

|
|

|
| 9
|
            
t1,3{3,3,3,3,3,3}
Bicantellated 7-simplex
|

|

|

|

|

|

|
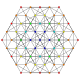
| 10
|
            
t2,3{3,3,3,3,3,3}
Tritruncated 7-simplex
|

|

|
|

|

|

|
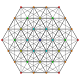
| 11
|
            
t0,4{3,3,3,3,3,3}
Stericated 7-simplex
|

|

|
|

|

|

|
| 12
|
            
t1,4{3,3,3,3,3,3}
Biruncinated 7-simplex
|

|

|

|

|

|

|
| 13
|
            
t2,4{3,3,3,3,3,3}
Tricantellated 7-simplex
|

|

|

|

|

|

|
| 14
|
            
t0,5{3,3,3,3,3,3}
Pentellated 7-simplex
|

|

|
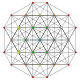
|

|

|

|
| 15
|
            
t1,5{3,3,3,3,3,3}
Bistericated 7-simplex
|
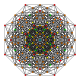
|

|

|

|
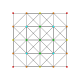
|
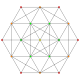
|
| 16
|
            
t0,6{3,3,3,3,3,3}
Hexicated 7-simplex
|

|

|

|

|

|

|
| 17
|
            
t0,1,2{3,3,3,3,3,3}
Cantitruncated 7-simplex
|

|

|

|

|

|

|
| 18
|
            
t0,1,3{3,3,3,3,3,3}
Runcitruncated 7-simplex
|

|

|

|
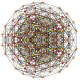
|

|

|
| 19
|
            
t0,2,3{3,3,3,3,3,3}
Runcicantellated 7-simplex
|

|

|

|

|

|

|
| 20
|
            
t1,2,3{3,3,3,3,3,3}
Bicantitruncated 7-simplex
|

|

|

|
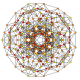
|
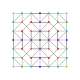
|

|
| 21
|
            
t0,1,4{3,3,3,3,3,3}
Steritruncated 7-simplex
|

|

|

|

|

|

|
| 22
|
            
t0,2,4{3,3,3,3,3,3}
Stericantellated 7-simplex
|

|

|
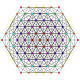
|

|

|

|
| 23
|
            
t1,2,4{3,3,3,3,3,3}
Biruncitruncated 7-simplex
|

|

|

|

|

|

|
| 24
|
            
t0,3,4{3,3,3,3,3,3}
Steriruncinated 7-simplex
|
|

|

|

|
|

|
| 25
|
            
t1,3,4{3,3,3,3,3,3}
Biruncicantellated 7-simplex
|

|

|

|

|

|

|
| 26
|
            
t2,3,4{3,3,3,3,3,3}
Tricantitruncated 7-simplex
|

|

|

|

|

|
|
| 27
|
            
t0,1,5{3,3,3,3,3,3}
Pentitruncated 7-simplex
|

|

|

|
|
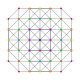
|

|
| 28
|
            
t0,2,5{3,3,3,3,3,3}
Penticantellated 7-simplex
|

|

|

|
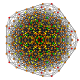
|

|

|
| 29
|
            
t1,2,5{3,3,3,3,3,3}
Bisteritruncated 7-simplex
|

|

|

|

|

|

|
| 30
|
            
t0,3,5{3,3,3,3,3,3}
Pentiruncinated 7-simplex
|
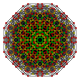
|

|

|

|

|

|
| 31
|
            
t1,3,5{3,3,3,3,3,3}
Bistericantellated 7-simplex
|

|

|

|

|

|

|
| 32
|
            
t0,4,5{3,3,3,3,3,3}
Pentistericated 7-simplex
|

|

|
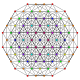
|

|

|
|
| 33
|
            
t0,1,6{3,3,3,3,3,3}
Hexitruncated 7-simplex
|

|

|

|

|

|
|
| 34
|
            
t0,2,6{3,3,3,3,3,3}
Hexicantellated 7-simplex
|

|

|

|
|

|

|
| 35
|
            
t0,3,6{3,3,3,3,3,3}
Hexiruncinated 7-simplex
|

|

|

|

|

|
|
| 36
|
            
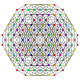
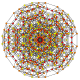
t0,1,2,3{3,3,3,3,3,3}
Runcicantitruncated 7-simplex
|

|

|
|
|

|

|
| 37
|
            
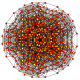
t0,1,2,4{3,3,3,3,3,3}
Stericantitruncated 7-simplex
|

|

|

|
|

|

|
| 38
|
            
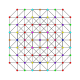
t0,1,3,4{3,3,3,3,3,3}
Steriruncitruncated 7-simplex
|

|

|

|

|
|

|
| 39
|
            
t0,2,3,4{3,3,3,3,3,3}
Steriruncicantellated 7-simplex
|

|

|
|
|

|

|
| 40
|
            
t1,2,3,4{3,3,3,3,3,3}
Biruncicantitruncated 7-simplex
|

|

|

|

|

|
|
| 41
|
            
t0,1,2,5{3,3,3,3,3,3}
Penticantitruncated 7-simplex
|

|

|

|

|

|

|
| 42
|
            
t0,1,3,5{3,3,3,3,3,3}
Pentiruncitruncated 7-simplex
|

|

|

|
|

|

|
| 43
|
            
t0,2,3,5{3,3,3,3,3,3}
Pentiruncicantellated 7-simplex
|

|

|

|

|

|

|
| 44
|
            
t1,2,3,5{3,3,3,3,3,3}
Bistericantitruncated 7-simplex
|

|

|

|

|

|

|
| 45
|
            
t0,1,4,5{3,3,3,3,3,3}
Pentisteritruncated 7-simplex
|

|

|

|

|
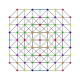
|

|
| 46
|
            
t0,2,4,5{3,3,3,3,3,3}
Pentistericantellated 7-simplex
|

|

|

|

|

|

|
| 47
|
            
t1,2,4,5{3,3,3,3,3,3}
Bisteriruncitruncated 7-simplex
|

|

|
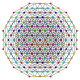
|

|

|

|
| 48
|
            
t0,3,4,5{3,3,3,3,3,3}
Pentisteriruncinated 7-simplex
|

|

|

|
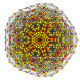
|

|
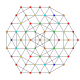
|
| 49
|
            
t0,1,2,6{3,3,3,3,3,3}
Hexicantitruncated 7-simplex
|

|

|

|

|

|

|
| 50
|
            
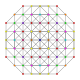
t0,1,3,6{3,3,3,3,3,3}
Hexiruncitruncated 7-simplex
|

|

|

|

|
|

|
| 51
|
            
t0,2,3,6{3,3,3,3,3,3}
Hexiruncicantellated 7-simplex
|

|

|

|

|

|

|
| 52
|
            
t0,1,4,6{3,3,3,3,3,3}
Hexisteritruncated 7-simplex
|

|

|

|

|

|

|
| 53
|
            
t0,2,4,6{3,3,3,3,3,3}
Hexistericantellated 7-simplex
|

|

|

|

|

|

|
| 54
|
            
t0,1,5,6{3,3,3,3,3,3}
Hexipentitruncated 7-simplex
|

|

|

|

|

|

|
| 55
|
            
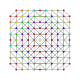
t0,1,2,3,4{3,3,3,3,3,3}
Steriruncicantitruncated 7-simplex
|

|

|

|

|
|

|
| 56
|
            
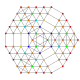
t0,1,2,3,5{3,3,3,3,3,3}
Pentiruncicantitruncated 7-simplex
|

|

|

|

|

|
|
| 57
|
            
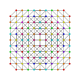
t0,1,2,4,5{3,3,3,3,3,3}
Pentistericantitruncated 7-simplex
|

|

|

|

|
|

|
| 58
|
            
t0,1,3,4,5{3,3,3,3,3,3}
Pentisteriruncitruncated 7-simplex
|

|

|
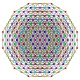
|

|

|

|
| 59
|
            
t0,2,3,4,5{3,3,3,3,3,3}
Pentisteriruncicantellated 7-simplex
|

|

|
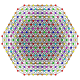
|

|

|
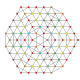
|
| 60
|
            
t1,2,3,4,5{3,3,3,3,3,3}
Bisteriruncicantitruncated 7-simplex
|

|

|

|

|

|

|
| 61
|
            
t0,1,2,3,6{3,3,3,3,3,3}
Hexiruncicantitruncated 7-simplex
|

|

|

|

|

|

|
| 62
|
            
t0,1,2,4,6{3,3,3,3,3,3}
Hexistericantitruncated 7-simplex
|

|

|

|

|
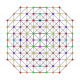
|

|
| 63
|
            
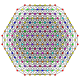
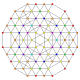
t0,1,3,4,6{3,3,3,3,3,3}
Hexisteriruncitruncated 7-simplex
|

|

|
|

|

|
|
| 64
|
            
t0,2,3,4,6{3,3,3,3,3,3}
Hexisteriruncicantellated 7-simplex
|

|

|

|

|

|

|
| 65
|
            
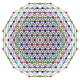
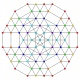
t0,1,2,5,6{3,3,3,3,3,3}
Hexipenticantitruncated 7-simplex
|

|

|
|

|

|
|
| 66
|
            
t0,1,3,5,6{3,3,3,3,3,3}
Hexipentiruncitruncated 7-simplex
|

|

|

|

|

|

|
| 67
|
            
t0,1,2,3,4,5{3,3,3,3,3,3}
Pentisteriruncicantitruncated 7-simplex
|

|

|

|
|

|
|
| 68
|
            
t0,1,2,3,4,6{3,3,3,3,3,3}
Hexisteriruncicantitruncated 7-simplex
|

|

|

|
|

|

|
| 69
|
            
t0,1,2,3,5,6{3,3,3,3,3,3}
Hexipentiruncicantitruncated 7-simplex
|
|

|

|

|

|

|
| 70
|
            
t0,1,2,4,5,6{3,3,3,3,3,3}
Hexipentistericantitruncated 7-simplex
|

|

|

|

|

|

|
| 71
|
            
t0,1,2,3,4,5,6{3,3,3,3,3,3}
Omnitruncated 7-simplex
|

|

|

|
|

|

|