Wikipedia talk:WikiProject Mathematics/Archive/2010/Nov

Analytic number theory spruce up

I'd really like to make the analytic number theory up to scratch - it currently reads like a random assortment of paragraphs from a textbook, with no real structure or cohesion. I've started a discussion on the talk page, and edits will be happening over the next few days - more eyes and opinions welcome. Joth (talk) 11:27, 27 October 2010 (UTC)

Please do -- it needs it. I suggest a userpage draft until you can get it as long as the current page (ish). CRGreathouse (t | c) 00:08, 31 October 2010 (UTC)

Negative and non-negative numbers

FYI, Negative and non-negative numbers has been requested to be renamed. 76.66.203.138 (talk) 04:56, 31 October 2010 (UTC)

Diagram of syntactic entities

This diagram shows the syntactic entities which may be constructed from formal languages. The symbols and strings of symbols may be broadly divided into nonsense and well-formed formulas. A formal language can be thought of as identical to the set of its well-formed formulas. The set of well-formed formulas may be broadly divided into theorems and non-theorems. However, quite often, a formal system will simply define all of its well-formed formula as theorems.

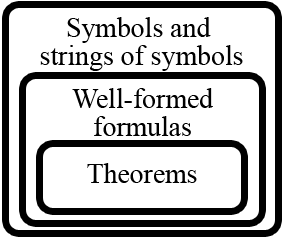
We have yet another pissing match featuring Arthur and Hans. We have long established that there is an ongoing problem with mathematics articles being inaccessible to readers, with no meaningful progress on that issue. I have created this diagram so as to help in that regard. However, it is apparently "silly" and "too simple" to be useful. Of course, by "useful" Arthur means "useful to him." I am pretty sure that "silly" is meaningless insofar as mathematics are concerned. Perhaps some other editors could provide some meaningful constructive input to the situation, something Hans and Arthur never do, at least not until after a great deal of drama. Of course I, and Hofstadter thought that something like this was perfectly illustrative. So lets see what is so terrible about it. I believe the biggest problem is pedantism.Greg Bard (talk) 21:10, 23 October 2010 (UTC)

Is it just me or does that diagram get larger and larger every time I see it. And the text below has turned into a mini essay. I tried to cut down the size to half the linear dimension once but obviously in vain - soon we'll be able to read it from the other end of a hall. Dmcq (talk) 21:46, 23 October 2010 (UTC)

(ec) What's good about it. If the diagram is accurate, then what it says is the following:

1. All well-formed formulas are "strings of symbols".

   In fact, only in some finitary languages, but we'll let that go, for the moment.

2. All theorems are well-formed formulas.

   (In the picture caption) According to Hofstadter, "quite often" all well-formed formulas are theorems.

   As far as I can tell, Hofstadter is the only one who believes that,

Finally, in what articles do you think it appropriate? I would say that, at most well-formed formula and theorem, and I have doubts about "theorem". — Arthur Rubin (talk) 21:57, 23 October 2010 (UTC)

Dmcq has excellent points. There are lots of graphical improvements to make, including making it SVG instead of PNG, and making the lines much thinner. It's useful as an overview for new readers who may find the terminology hard to conceptualize; it would be even more useful if it contained examples from each of the classes (e.g., from the inside out: "(3·3)+(4·4)=(5·5)", "(2+2)=17", "83(+)3(", and ""). The caption-cum-essay must be trimmed brutally; captions are not supposed to be self-contained mini-articles. Arthur is right that it is nonsense to claim that most formal systems make all wffs into theorems (which is often taken as the formal definition an inconsistent system). –Henning Makholm (talk) 01:50, 24 October 2010 (UTC)

Irrespective of the merits of this diagram in this particular discussion, Greg you need to quit it with the Hans and Arthur never contribute anything. It is patently false and reveals _you_ to be the drama queen. Be civil, or keep quiet. 71.233.148.24 (talk) 22:30, 23 October 2010 (UTC)

I don't think it's true in practice that all theorems are well formed formulas. Maybe all formal theorems are, and maybe most or all theorems could be formalized as such, but actual theorems are generally expressed as sequences of words in a natural language. —David Eppstein (talk) 02:16, 24 October 2010 (UTC)

The diagram should not be taken as more than clarifying how the words are used within the specific field of formal theories and metamathematics. That ought to be clear if it is only used in articles within that field, though it might not hurt if the caption pointed it out (without the caption growing excessive). –Henning Makholm (talk) 14:17, 24 October 2010 (UTC)

Greg - I would like to know where exactly you think Hoftstadter says that a formal system will "often" define all of its well-formed formulas as theorems. A quote with a section name so that I can find the passage in my Penguin 1980 edition of GEB would be useful. In the discussion of the pq-system in the section "Double-Entendre!" in Chapter II "Meaning and Form in Mathematics" Hofstadter says:

"Among the well-formed strings occur the theorems. These are defined by an axiom schema and a rule of production ... Notice, therefore, that all false additions ... are mapped into strings which are well formed, but which are not theorems." (my italics)

This does not seem to agree with your claim about Hofstadter's views. Gandalf61 (talk) 18:09, 24 October 2010 (UTC)

Greg — stop the personal insults — they are inappropriate, counterproductive, unwanted here, against policy and sanctionable. Paul August ☎ 11:29, 31 October 2010 (UTC)

Disagreement on whether to include coverage of a proof in the lead at 0.999...

There is a dispute at Talk:0.999...#Refining the paragraph over whether the lead, or more precisely the first paragraph, should include part or all of a proof of 0.999... equalling one. Other opinions on this would be welcome.--JohnBlackburne^words_deeds 12:22, 31 October 2010 (UTC)

See also Talk:0.999...#RfC:_coverage_of_proofs_in_the_lead. The requested explanation is not required to be in the first paragraph, it's just to have one paragraph somewhere in the lead. Diego Moya (talk) 12:48, 31 October 2010 (UTC)

incorrect claim for Pelletier's use of "milliard"

According to Jacques Pelletier du Mans, the following claim in Long and short scales is wrong:

Jacques Pelletier du Mans used the name milliard (“milliart”) for "Million de Millions", i.e. 10¹².

Apparently the following is also wrong and is apparently an incorrect and OR interpretation of what Google shows from David Eugene Smith's History of Mathematics:

The majority of scientists either continued to say "thousand million" or changed the meaning of the Pelletier term, milliard, from "million of millions" down to "thousand million". --Espoo (talk) 21:13, 1 November 2010 (UTC)

This is probably best taken up at Talk:Long and short scales, —Mark Dominus (talk) 22:06, 1 November 2010 (UTC)

Convergence test for improper integrals

It seems to me that no such articles exist as of now, at least improper integral doesn't mention the method of determining convergence. Besides, Abel's test or Dirichlet test should describe their applicability to improper integrals in addition to series.--Netheril96 (talk) 11:40, 2 November 2010 (UTC)

Proof of the chain rule

Useful link relevant to this discussion: Chain rule.

Opinions of this edit? (In my view, this rewrite gives a clearer way of explaining the proof.) Michael Hardy (talk) 03:37, 31 October 2010 (UTC)

Some typos and other matters have been fixed since I posted what you see above, so judge according to the latest version. Michael Hardy (talk) 04:46, 31 October 2010 (UTC)

Well the proof is even easier than that. For any coordinate (real valued function) y on a line (e.g. the real line) and any point p, denote by dy_p the equivalence class of y-y(p)1 (where 1 is the constant function, with value 1) modulo functions vanishing at p to higher order. If y=f(x) (i.e. y = f ⚬ x for some other coordinate x on the same line and some f:R→ R) then the definition of differentiability of f at x(p) ensures that dy_p = f'(x(p)) dx_p because f(x)-f(x(p))1 differs from f'(x(p))(x-x(p)1) by a function vanishing at p to higher order.

The chain rule is an immediate consequence. If u = g(y) then, omitting subscripts, du = g'(y)dy= g'(f(x))f'(x) dx.

The original argument formalizes this basic idea without discussing the conceptual meaning. Geometry guy 00:55, 2 November 2010 (UTC)

I hope you're not proposing to write it that way in the article, as the first proof to be read by those learning calculus! Michael Hardy (talk) 16:34, 2 November 2010 (UTC)

No I am not proposing to write it that way, but why do you presume that the article should be written as the first proof to be read by those learning calculus? This is an encyclopedia, not a textbook. Geometry guy 22:14, 2 November 2010 (UTC)

Well our primary target as reader is still the (educated) general public and not mathematician or scientists. Or to put it this way we are first and foremost a general purpose encyclopedia (like britannica) and only secondly a special subject encyclopedia as well. For our primry target (general public) it seems to be a good idea not to expect specific math knowledge beyond that of a "calculus learner". Generally you could argue anyhow that first chapters of an article usually should pick the most accessible approach/lowest abstraction level that still allows correct description. More abstract approaches can follow in later chapters. In other words it is not a question of encyclopedia versus textbook, but a question of what amount of knowledge is reasonable to assume for the majority of our readers (of math articles).--Kmhkmh (talk) 23:33, 2 November 2010 (UTC)

Should we assume the same level of knowledge throughout a single article? Geometry guy 23:41, 2 November 2010 (UTC)

No of course not, as i said later on in the article there can be more advanced treatments of the same subject (assuming a different level of knowledge), but normally we should not start the article with those more advanced treatments of the article's subject.--Kmhkmh (talk) 23:47, 2 November 2010 (UTC)

Okay that's good. The question here is then: to what extent should an advanced proof inspire the presentation of an elementary proof? It is not an easy question. But a related question would be whether an elementary proof should be based on conceptual misunderstandings for simplicity. None of these questions are easy to answer! Geometry guy 23:58, 2 November 2010 (UTC)

Well for the elementary proof and its presentation accessibility is the key. Whether behind the scenes it draws inspirations from a more abstract viewpoint/approach/concept or not, doesn't really matter that much imho, that's a secondary question depending on skills and preferences of the authors working on the article. The primary issue that all authors should adhere to regardless of their personal preferences is to provide as much accessibility as possible for the elementary proofs or treatments. Btw. accessibility (ideally) includes motivation/inspiration as well, i. e. the elementary proof and its representation should not only be accessible regarding its formal individual steps, but his overall direction and the "proof idea" should (ideally) "make sense" to the less advanced reader as well.--Kmhkmh (talk) 03:45, 3 November 2010 (UTC)--Kmhkmh (talk) 03:45, 3 November 2010 (UTC)

What concerns me more than the proof is the hideous dy/dx notation. Why would you put the d in upright type? Where the heck does this come from? Would anyone mind if I got rid of it? It's a typographical abomination. Ozob (talk) 11:32, 2 November 2010 (UTC)

I think it's done by physicists, and some of them might not even know that some people don't do it that way. I've seen an argument adduced in its favor: One might want to use the letter d as a variable, while the "upright d" is still used in the formation of these differential operators. But I wouldn't mind at all getting rid of that notation in this article. Michael Hardy (talk) 16:33, 2 November 2010 (UTC)

To Geometry guy: You asked "... whether an elementary proof should be based on conceptual misunderstandings for simplicity.". Absolutely not. We should never take a falsity as a premise, unless we are explicitly doing an approximate calculation or reductio ad absurdum. Passing a falsehood off as the truth, even implicitly, is lying and will harm the readers. JRSpriggs (talk) 08:07, 3 November 2010 (UTC)

The earlier proof, which fairly close to what Geometry guy proposes, more easily generalizes to other situations. The new proof, however, is arguably somewhat simpler and probably closer to what can be found in a first year calculus textbook, despite initially being based on a fallacy. I think, once the original proof is streamlined a bit, both proofs add value to the article. One is more useful to those just starting out, and the other useful to those encountering this material a second time in or after a first course on analysis. Sławomir Biały (talk) 10:48, 3 November 2010 (UTC)

I've added a corrected version of the old proof, in addition to the new one. A separate issue with the article, that also effects the presentation of the proof, is the lack of a proper statement of the chain rule for a function between two Euclidean spaces. This should be in the several variables section, I should think. Sławomir Biały (talk) 11:25, 3 November 2010 (UTC)

I quite agree that generalizations and more advanced results should inform our treatment of elementary ones, and I think it is an excellent idea to present both proofs. Geometry guy 00:31, 6 November 2010 (UTC)

Help! Adjoint representation

Hi, over at the disambiguation pages with links project, we've come across the disambiguation page Adjoint representation, with 67 links that need to be pointed to the correct article. I start looking into this, and then the headaches start. Could an expert help us out? Thanks, --JaGa^talk 13:07, 3 November 2010 (UTC)

If the linking article talks about adjoint representations of a group - any group - (as quantum chromodynamics talks about adjoint representation of the SU(3) gauge group) link to adjoint representation of a Lie group; if the linking article talks about adjoint representations of an algebra, link to adjoint representation of a Lie algebra. It is true that what I have quoted is not the link text; perhaps it ought to be. But some such text should be found about 95% of the time, by searching on adjoint - and if you get it wrong, it doesn't matter all that much. The two terms exist because the two things are closely related, by what is called a functor, and the two articles link to each other. Septentrionalis PMAnderson 14:43, 3 November 2010 (UTC)

Actually you should get rid of it as flawed (only two links out), redirect to Adjoint representation of a Lie group which has more cases, and have a hatnote there to adjoint endomorphism which is where Adjoint representation of a Lie algebra redirects. (Hatnote back also.) That would be step one. Second would be to sort out the cases where it is definitely a Lie algebra: for a first pass just do those that say "algebra" in the page title. Then there are physics pages, and essentially it doesn't matter so much for those pages. Charles Matthews (talk) 15:02, 3 November 2010 (UTC)

I cannot agree. The link in the dab page should be changed; but it is suboptimal to link from Universal enveloping algebra to Adjoint representation of a Lie group. The two concepts are related, but they have different meanings and different formulae; a few cases of the wrong link are acceptable, but we should not do it systematically. Septentrionalis PMAnderson 15:12, 3 November 2010 (UTC)

But that was not what I was suggesting: universal enveloping algebra falls under those I was suggesting should be piped to adjoint endomorphism. Charles Matthews (talk) 09:13, 4 November 2010 (UTC)

Hurm. So, I'm looking at a few of these: Special unitary group, Color charge, and Root system. I'm thinking it should go like this:

1. Special unitary group is a reference to an Infinitesimal generator, which is "an element of the Lie algebra associated to a Lie group", so link to Adjoint representation of a Lie group
2. Color charge is a physics article that talks about groups; Adjoint representation of a Lie group
3. Root system deals with both groups and algebras, so I was thinking of invoking WP:INTDABLINK and linking intentionally to the dab page Adjoint representation (disambiguation).

What do you think? (Also, I'm under the impression, unless it specifically mentions algebras, use the group article). --JaGa^talk 01:42, 5 November 2010 (UTC)

Partial fractions

Partial fraction is quite a mess at the moment. One of the major issues is an overabundance of disorganised examples. I've tried to condense the principles and procedures behind these examples into a concise description. Some help with cleaning up the article, as well as a review of my edits, would be appreciated; my understanding of polynomials does not extend far beyond high school. These were my changes. —Anonymous Dissident^Talk 13:47, 2 November 2010 (UTC)

I think that most of the urgent problems have been fixed. A certain amount of this is probably in the eye of the beholder, though. If someone else wants to drop by and check out the changes, I certainly wouldn't object. Sławomir Biały (talk) 16:05, 8 November 2010 (UTC)

Inexact differential

The article titled Inexact differential could use some work. The concept seems to be fairly general but the first sentence narrows it down to thermodynamics. Maybe written by someone who's studied only thermodynamics? Michael Hardy (talk) 00:00, 5 November 2010 (UTC)

I have only encountered inexact differentials in thermodynamics. Any other example?Netheril96 (talk) 02:59, 5 November 2010 (UTC)

...and also Exact differential

...could use some work. It now starts like this:

A mathematical differential dQ is said to be exact, as contrasted with an inexact differential, if the differentiable function Q exists.

But you can't call it dQ, unless Q exists. I'd modify the sentence if I were sure what genus the concept should belong to. 1-forms, maybe? Michael Hardy (talk) 00:07, 5 November 2010 (UTC)

Something like this would work (but see below):

"A mathematical differential is said to be exact if it is of the form dQ for some differentiable function Q.

provided it's clear what a "mathematical differential" in general is. There's a link, but I hesitate to be sure that it's the right one.

Well obviously, it is a 1-form, but applied mathematics textbooks are not very helpful sources in this respect! Geometry guy 00:59, 5 November 2010 (UTC)

To be more precise, quite often the notation dQ is used in applied math for a closed 1-form, where Q exists locally, but not globally. A practical example would be d(log x) = dx/x, where a choice of branch of logarithm is needed to integrate the 1-form. Geometry guy 00:28, 6 November 2010 (UTC)

In fact, in thermodynamics dQ is the standard notation for the differential of the heat Q, but as is well known, Q is not a well-defined quantity (i.e. dQ is not an exact — or even closed — 1–form), because it need not be conserved in a cyclical process, unlike the entropy S that is related to Q via dS=dQ/T. Arcfrk (talk) 21:31, 7 November 2010 (UTC)

I suppose this is sort of like the notation dθ for the interesting differential on the unit circle. It seems worth mentioning somewhere that occasionally notation is abused and inexact differentials are sometimes written as if they are exact. Ozob (talk) 12:16, 8 November 2010 (UTC)

Are they usually locally exact in such cases? Michael Hardy (talk) 20:56, 8 November 2010 (UTC)

"Locally exact" = "closed", and I believe differentials in applied math are often locally exact. However, Arcfrk gives an example where a differential dQ is not even closed. The notation is effectively wishful thinking: we want dQ to be the differential of a heat function Q, but sometimes it simply isn't! Geometry guy 22:20, 8 November 2010 (UTC)

Group of rational points on the unit circle

Should this article be merged with Circle group or what? (I didn't know about circle group article till later.)24.7.28.186 (talk) 16:08, 7 November 2010 (UTC)

The two groups have very different structures and as such deserve different articles. A see also link in Circle group seems appropriate.--Salix (talk): 18:43, 7 November 2010 (UTC)

The group of rational points on the unit circle is a relatively small subgroup of the circle group. JRSpriggs (talk) 21:39, 7 November 2010 (UTC)

Semi-infinite stub created

I've just created a stub for semi-infinite, but it's rather out of my own areas of maths, so if anyone can give feedback or help improve it, I'd be very grateful! (Following the advice here. ☻) Pit-trout (talk) 16:16, 7 November 2010 (UTC)

Honestly I'm not in favor of jargon articles. If there's not a well-specified concept being described, the article should probably be deleted. (I note in passing that you missed the engineering meaning of semi-inifinite.) --Trovatore (talk) 18:42, 7 November 2010 (UTC)

Actually, if there's no well-defined meaning the page should probably become a dab page. CRGreathouse (t | c) 04:44, 8 November 2010 (UTC)

No, I really don't agree. That just encourages people to link it, and it shouldn't be linked. If it's not clear, explain it inline. Explaining jargon by wikilinks is a bad idea — see the horrendous if and only if. --Trovatore (talk) 04:51, 8 November 2010 (UTC)

Of course people shouldn't like dab articles at all... CRGreathouse (t | c) 14:22, 8 November 2010 (UTC)

I generally agree with Trovatore about this. Moreover, this is bad jargon. Every "semi-infite" set is infinite. A lot of people are already confused about the meaning of infinity and think that a bounded set of reals can't be infinite. This kind of ill-considered jargon only fuels the confusion. Hans Adler 11:57, 8 November 2010 (UTC)

However bad the term may be, it is in wide use. Our encyclopedia should say something about what it means, supposing that a reliable and authoritative source can be found. The same page might cover the even more peculiar term "quarter-infinite". I also see that we have three articles that use the bizarre term "biunique".

Perhaps it should just redirect to the article about semi-boneless hams. —Mark Dominus (talk) 16:14, 8 November 2010 (UTC)

I guess my original wording about lack of "no single formal definition" was bad: I meant that it had multiple definitions, not none! It's certainly a well-accepted and widely-used technical term, as a quick search on titles at www.arxiv.org (or other cataglogues of the literature) reveals, and no more jargony than plenty of other technical concepts with several meanings (open, bounded, …) (Re which, Trovatore: I was only writing up the definitions I knew; I hope someone else will document the engineering usage, if it's widely enough used.)

A disambiguation page could make a lot of sense, since the meanings afaics seem all seem to fall into a few classes: subsets of total orders, subsets of Euclidean spaces, and the kind occurring in semi-infinite programming.

It's true, and unfortunate, that it can be confusing for people not familiar with the technical background; but surely that's more an argument for where to use it (only in technical contexts, not in explanations for the lay reader) rather than for not documenting the technical term? Pit-trout (talk) 17:51, 8 November 2010 (UTC)

Wikipedia is not a dictionary. Mathematical articles should be written only when there's something interesting to say about the mathematics, not merely to define a term. --Trovatore (talk) 19:53, 8 November 2010 (UTC)

If there were a separate article on semi-infinite intervals I'd consider making this a disambiguation page. If I were somewhat confident that there ought to be such an article, I'd create it. Michael Hardy (talk) 20:48, 8 November 2010 (UTC)

I have alerted Wikipedia talk:WikiProject Disambiguation about this discussion; they have have views on the proper fate of the article (disambiguation page, article, deletion, or something else). CRGreathouse (t | c) 20:51, 8 November 2010 (UTC)

Semi-infinite programming

Mathematical Reviews classifies "semi-infinite programming" as 90C34 in its Mathematics Subject Classification (MSC2010). Thanks Kiefer.Wolfowitz (talk) 16:51, 8 November 2010 (UTC)

Yet another semi-infinite stub?

The T.O.C. of this page listed a section titled "Semi-infinite stub created". In the T.O.C., you can't tell that "semi-infinite" is a link, so I thought: Yet another of those interminable War-and-Peace-length ("semi-infinite") articles where if you somehow succeed in scrolling all the way to the bottom, it says "This article is a stub." Usually I just delete the "stub" tag. But I guess that's not what it is this time. Michael Hardy (talk) 20:34, 8 November 2010 (UTC)

Article for deletion: Sacks spiral

Some discussion is going on at Wikipedia:Articles for deletion/Sacks spiral. Will Orrick (talk) 15:48, 8 November 2010 (UTC)

Padé approximant

Padé approximant tells about existence, uniqueness and usefulness, but not a hint about how to construct one, unless I'm too thick to see it. (I looked about some with Google, with no better luck.) Is it a black art? —Tamfang (talk) 16:21, 10 November 2010 (UTC)

Let the approximant be R(x)=N(x)/D(x) as defined in the article with the coefficients of N(x) and D(x) as yet undetermined. Compute f(x)D(x)–N(x) to order m+n in x. Set all coefficients equal to zero and solve the resulting system of linear equations. See also P. Wynn, The Epsilon Algorithm and Operational Formulas of Numerical Analysis, Mathematics of Computation, Vol. 15, No. 74 (Apr., 1961), pp. 151-158. Published by: American Mathematical Society. Stable URL: http://www.jstor.org/stable/2004221. Will Orrick (talk) 20:20, 10 November 2010 (UTC)

Does "Compute f(x)D(x)–N(x) to order m+n in x" mean compute m+n derivatives? —Tamfang (talk) 22:37, 10 November 2010 (UTC)

It's really just polynomial multiplication: D(x) is the polynomial of degree n with coefficients 1, q₁, ..., q_n from the article; the function you are approximating, f(x), is actually an infinite series, but you can truncate it after the x^n+m term; N(x) is the polynomial of degree m with coefficients p₀, p₁, ..., p_m from the article. Mutliply f(x) and D(x), and subtract N(x). Then collect terms, discarding any of degree higher than m+n. Set the coefficients of x⁰, x¹, ..., x^m+n equal to zero. You now have a system of m+n+1 linear equations in m+n+1 unknowns, namely the coefficients p_i and q_j. In general there will be a unique solution, unless the system happens to be singular.

This is the most naive approach, and can be cumbersome if m+n is big. The article I mentioned describes an iterative approach. Will Orrick (talk) 23:27, 10 November 2010 (UTC)

A nice algebraic/symbolic account occurs in Chapter 5.9 (2nd ed.) of this: von zur Gathen, J.; Gerhard, J. (2003), Modern Computer Algebra, Cambridge University Press, ISBN 0-521-82646-2. Best regards, Kiefer.Wolfowitz (talk) 22:08, 10 November 2010 (UTC)

Really I meant to urge that the article (rather than this page) should have a better explanation! —Tamfang (talk) 03:35, 11 November 2010 (UTC)

Plus I think the straightforward approach above though it may be cumbersome is probably a better explanation, the iterative approach could then be mentioned as an optimization. I think I'll have to look at that article to see why anyone would want m+n to be large though, I don't think I've seen one of order more than about 15 myself. Dmcq (talk) 13:46, 11 November 2010 (UTC)

Shapley–Folkman lemma

In combinatorial convex geometry, the Shapley–Folkman lemma concerns the approximate convexity of Minkowski sums of non-convex sets; the Shapley–Folkman lemma is used in mathematical economics, optimization, and probability.

The article has received a substantial (Wikipedia) peer-review. The additional suggestions (including article assessment) of mathematicians would be especially helpful now.

Thanks! Best regards, Kiefer.Wolfowitz (talk) 19:23, 11 November 2010 (UTC)

Chebyshev cube root

Chebyshev cube root needs references. There seem to be five books that can be found via Google, and some papers. If someone can figure out which parts of which sources should be cited in which parts of the article before I or someone else gets to it, that would be useful. Michael Hardy (talk) 16:50, 12 November 2010 (UTC)

Opperman's conjecture

Opperman's conjecture, concerning the distribution of primes, is an orphan, i.e. no other articles link to it except the list of mathematics articles. Michael Hardy (talk) 05:41, 13 November 2010 (UTC)

WP:CHALLENGE and WP:BURDEN

I may be wrong, but I think we have something like a consensus that things that can be found in every textbook that covers an article's topic do not need inline citations. Motivated by a dispute at logarithm and by the suspicion that wikipedantry helped create the climate in which some rather experienced editors resort to plagiarism because they feel V and NOR leave them no other choice, I have proposed an addition to WP:V. See WT:V#When a reliable source is required. Hans Adler 16:44, 13 November 2010 (UTC)

MuPAD

Does anyone know the status of MuPAD? Has it been discontinued? I have started a discussion on this at Talk:MuPAD. Yaris678 (talk) 17:10, 13 November 2010 (UTC)

OEIS prefix broken

The OEIS interwiki prefix has been broken: Wikipedia:Village pump (technical)#On-Line Encyclopedia of Integer Sequences links. PrimeHunter (talk) 22:58, 13 November 2010 (UTC)

Template:Infobox integer sequence

I noticed {{Infobox integer sequence}} being applied to some articles. I'm just pointing out its availability, without comment as to whether it's appropriate. — Arthur Rubin (talk) 18:23, 14 November 2010 (UTC)

Please create a stub for class representative (mathematics), or somehow fix the class representative disambiguation page

Hello,

I'm a law student, and I created class representative as a redirect to lead plaintiff. Then I discovered that "class representative" is also a mathematical term. So, as a courtesy, I changed the redirect into a disambiguation page. However, I do not have any mathematical background, so I do not feel qualified to populate "your" section of the disambiguation page. Currently the page is not compliant with wikipedia stylistic rules. So I would like to invite someone here to fix "your" section of the dab page, either by creating a stub for class representative (mathematics), or by formatting your dab section some other way. Thanks.

-AGradman / talk / how the subject page looked when I made this edit 21:49, 14 November 2010 (UTC)

I don't think a separate stub is appropriate, rather a link to equivalence class at the new dab page is preferable. Sławomir Biały (talk) 22:19, 14 November 2010 (UTC)

FP candidate

A math related image has been nominated for FP. See Wikipedia:Featured picture candidates/Maze Generation for discussion.--RDBury (talk) 04:48, 15 November 2010 (UTC)

Withdrawn by nominator. Ozob (talk) 01:39, 16 November 2010 (UTC)

Formatting issues

At talk:Logarithm we have a discussion (prolonging a previous one at talk:complex number) about the markup of mathematical standalone formulas. DVdm and JohnBlackburne make it a point that standalone formulas like

log_b(x) = y (typed as log_''b''(''x'') = ''y'')

have to be formatted using <math> markup, such as

$\log _{b}(x)=y\,$ (typed as <math>\log_b(x) = y \,</math>)

Their main argument is WP:MOS, which says "An overriding principle is that style and formatting choices should be consistent within a Wikipedia article". I contest this point of view, based on the idea that using math markup (where not necessary) as opposed to HTML markup in standalone formulas, creates more inconsistencies than really necessary. Can someone with with a cool head please have a say? Jakob.scholbach (talk) 20:55, 18 November 2010 (UTC)

I think that display formulas may be done with either html or TeX, but I personally prefer the appearance of TeX. JRSpriggs (talk) 00:53, 19 November 2010 (UTC)

I agree with the original consistency argument. Formatting display formulas in TeX is a widespread convention on Wikipedia, which indeed makes HTML used in its place look odd.—Emil J. 10:50, 19 November 2010 (UTC)

Merger of Symbolic computation with Computer algebra system

See Talk:Symbolic computation#Merger with computer algebra system Yaris678 (talk) 14:01, 19 November 2010 (UTC)

Orthogonal basis

Someone changed Orthogonal basis from a redirect (Orthonormal basis) to a new article. The redirect was a bit dodgy because the concepts, while related, are different and the other article doesn't really cover the subject. On the other hand, the concepts are similar enough that they could be covered in the same article. Orthogonal bases often appear in contexts, such as orthogonal polynomials, where insisting on unit length would only introduce a lot of pesky square roots into computations, so they are a legitimate subject in their own right. If there is to be a separate article then the stub should be expanded and if not then material should be added to the other article, but it's not clear to me which way to go at this point.--RDBury (talk) 08:38, 18 November 2010 (UTC)

On general principles, the more general concept, which is here "orthogonal basis", should have the top-level article. Charles Matthews (talk) 09:29, 18 November 2010 (UTC)

I was the one who changed it, for some of the reasons mentioned above. It seems to me that content on orthogonal bases is more likely to be added now that the topic has its own stub, and it also helps the orthonormal basis article to not have to cover orthogonal bases as well. If the stub doesn't improve over time, then merging it back into orthonormal basis would certainly be reasonable. Jim.belk (talk) 22:11, 20 November 2010 (UTC)

The problem is that, in such cases, editors often don't realize/don't care about the 'companion' article, and thus both articles end up with very similar information, with one of the two usually ending up poorly written. This can make maintenance quite a bother. So beware ... While this can be kept under control with some strict policing, that can be harder to do with articles on 'popular' themes. such as this. linas (talk) 03:17, 21 November 2010 (UTC)

Scientific citation guidelines discussion

There's a discussion at Wikipedia talk:Scientific citation guidelines#Bringing this guideline in line with policy that may be of interest to others here. The short version is, an editor wants to change the guidelines to explicitly discourage the use of references to original research papers. —David Eppstein (talk) 20:04, 21 November 2010 (UTC)

Wikipedia:Scientific citation guidelines

(Just a courtesy note.) There has been some discussion recently about whether Wikipedia:Scientific citation guidelines needs to be updated to reflect current practice. This wikiproject is one of the projects that signed on to this guideline in the past. If you have any comments or concerns about the guideline, please feel free to comment at Wikipedia talk:Scientific citation guidelines.

If we decide that we don't want to be associated with the guideline any more, it would be possible to remove our project from the list at the top of the guideline page. However, keeping the guidelines up to date seems like a better option to me. — Carl (CBM · talk) 18:56, 22 November 2010 (UTC)

WP:MOSMATH

I was thinking about the formatting we use for the capital letter I to denote an interval; say I = [0,1]. I really don't like how this letter looks in this font. What about using the teletext font I instead? You get this by typing <tt>I</tt>. Which do you think looks better I = [0,1] or I = [0,1]? I know that $I=[0,1]$ and $\scriptstyle I=[0,1]$ are options, but the former has alignment problems and the latter looks more or less the same; except for the loading time and the other browser settings that people might have. What are your opinions on the matter? — Fly by Night (talk) 23:45, 22 November 2010 (UTC)

In published mathematics, we would never use a teletext font randomly like that. On Wikipedia you should use either an italic capital I (I) or put it in math mode $I\,$. Don't use the smaller size math mode in running text by invoking "scriptstyle". Usually italics is fine. You can't rely on anyone else seeing the page the way you see it, because of varying fonts, browser settings, browsers, operating systems, etc. So just stick to the tried-and-true. — Carl (CBM · talk) 23:49, 22 November 2010 (UTC)

From where I'm viewing this, the teletext version looks good, in that it has serifs where the italic I does not, and is slanted like the italic I. But I don't know how much of that is browser-dependent. Michael Hardy (talk) 00:36, 23 November 2010 (UTC)

My italic I has serifs. It's completely font dependent. For some people the teletype font will be Courier. — Carl (CBM · talk) 00:43, 23 November 2010 (UTC)

My italic I lacks serifs, so I agree with Hardy and Night (irresistible pun intended). Perhaps font dependency could also explain why some users see no incongruence between the notations $f\,\!$ and f for the same function, and others see a typographical travesty (c.f. earlier, much longer thread). Sławomir Biały (talk) 00:58, 23 November 2010 (UTC)

My italic I lacks serifs, but the teletype I does indeed appear to be slanted Courier. It looks peculiar. It's too short, since the top bar of the equals sign is just below the top bar of the I. And it's too blocky, because Courier is very much a slab serif font and the rest of the text, which I believe is in Helvetica, doesn't have any serifs at all. On the other hand maybe a teletype font is more legible despite its incongruity.

In general I would prefer that we avoid making fine typographical adjustments like these in Wikipedia articles. Our articles are not set in metal once and printed for all time; they get edited and updated and displayed on new browsers continually. Little tricks like this are hard to maintain and may become irrelevant or unsightly on newer software. Ozob (talk) 01:47, 23 November 2010 (UTC)

I've just logged on using Ubuntu which is a Linux based operating system, and the teletext I and the italic I are indistinguishable! :-( They're both just a straight line, sans-serif I think they call it. I'm using Google Chrome like I was last night on my Vista laptop. Interestingly; the font in the edit window is identical on both operating systems. — Fly by Night (talk) 12:07, 23 November 2010 (UTC)

"Residue on infinity"

Should Residue on infinity be moved to Residue at infinity? Michael Hardy (talk) 04:05, 24 November 2010 (UTC)

Uniqueness theorem

This article seems to be misnamed—presumably "uniqueness theorem" should be a disambiguation page pointing to this theorem among others. Anyone have any suggestions for a new name for this article? Also, what are some other important uniqueness theorems that a disambiguation page could point to? Jim.belk (talk) 02:00, 26 November 2010 (UTC)

The Picard–Lindelöf theorem on the uniqueness of the solution to a differential equation. —Mark Dominus (talk) 03:08, 26 November 2010 (UTC)

I moved it to uniqueness theorem for Poisson's equation. Most of the articles that linked to it plainly did not intend the uniqueness theorem for Poisson's equation, so I left most of the links to the article intact and made the newly created redirect page titled uniqueness theorem into a stub article. Work on it. Michael Hardy (talk) 06:49, 26 November 2010 (UTC)

Jacobi's theorem

• Can anybody add Carl Jacobi's “regions of equal area” in 1842 theorem to Jacobi's theorem? ––虞海 (Yú Hǎi) ✍ 07:23, 27 November 2010 (UTC)

Composite Number Factoring Theorem

Just "original research"? Michael Hardy (talk) 00:48, 26 November 2010 (UTC)

This appeared as a question on the help desk.--RDBury (talk) 20:15, 27 November 2010 (UTC)

Need an easier way into some of these maths pages

I got to http://en.wiki.x.io/wiki/Circle_group as a redirect of http://en.wiki.x.io/wiki/U(1) from a link in "Thus, for example, the electric charge is the generator of the U(1) symmetry of electromagnetism. " on http://en.wiki.x.io/wiki/Charge_(physics). I was expecting to see something like

U(1) is circular, U(2) is spherical, etc.

Instead I got the general treatment of circle groups, which is next to useless for a non-mathematician. —Preceding unsigned comment added by 202.63.53.14 (talk) 01:41, 28 November 2010 (UTC)

You seem to actually have gotten the most relevant page for explaining what a U(1) symmetry is in physics, namely a phase rotation of the involved fields.

That being said, it would be useful if circle group actually mentioned U(1) in the lead (I think this is actually required by the MoS since U(1) redirects there), when mentioning U(1) this would be a good place to also link to unitary group.TimothyRias (talk) 11:28, 28 November 2010 (UTC)

Done. Sławomir Biały (talk) 13:31, 28 November 2010 (UTC)

In higher dimensions, the group of rotational symmetries of an n-sphere is not U(n), it is the real special orthogonal group SO(n+1,R). It so happens that U(1) is isomorphic to SO(2,R), and SU(2) is the double cover of SO(3,R) i.e. it is isomorphic to SO(3,R) x {I, -I}. These relationships are accidental isomorphisms, and there is no simple generalisation of them to higher dimensions. Gandalf61 (talk) 12:20, 28 November 2010 (UTC)

To Gandalf61: SU(2) locally resembles SO(3,R) x {I, -I}, but globally they are different. If you make a 360° rotation, you end up on the other sheet. So SU(2) is path connected, unlike SO(3,R) x {I, -I}. JRSpriggs (talk) 14:56, 28 November 2010 (UTC)

I should also say that SU(2) is the universal cover of SO(3,R). JRSpriggs (talk) 15:17, 28 November 2010 (UTC)

Mathematical art & computer generated imagery

Hi, any mathematical modern art experts here? Ideas on Talk:Fractal_landscape#Fractal_images.2C_art.2C_landscapes.2C_surfaces.2C_etc. on how to manage the hierarchy for computer generated art/images and fractal arts, etc. will be appreciated. That topic does need help, as discussed there.

The Mathematics and art article goes way way back in time and seems stuck in golden ratios, etc. But there is serious and interesting mathematics used in the modern approaches to computer generated imagery and should probably be discussed in a more mathematical setting.

The computer generated imagery class of articles even had source code in them (e.g. see Orbit trap !) and I am cleaning those up now. But suggestions on the topic of "Math and modern art" which I do not know that well, will be appreciated. History2007 (talk) 03:21, 29 November 2010 (UTC)

WP:PMEX

I note that activity on WP:PMEX -- WikiProject Planet Math Exchange -- is at an all-time low. I still regularly stumble across topics where WP has no article, or a stub, while PM has a slow-to-load, hard-to-grok, but non-trivial article on the topic. It'd be nice to have WP:PMEX get functioning again ... linas (talk) 04:07, 29 November 2010 (UTC)

There was a licensing issue to do with the adoption of CC-by-SA here. But it does seem from http://planetmath.org/?op=license that that was only temporary. Charles Matthews (talk) 06:55, 29 November 2010 (UTC)

A statistician's view on Z-factor...

...would be helpful. Thanks, Geometry guy 22:12, 29 November 2010 (UTC)

A few missing Canadian mathematicians

In case someone here is looking for something to do: I was browsing the web site for the Canada Research Chair program today, and came across a few mathematicians who seem clearly notable enough to have articles here, but don't: Nantel Bergeron, David Brydges, George A. Elliott, J. F. Jardine, Stephen S. Kudla, François Lalonde, Bojan Mohar, Sujatha Ramdorai, Thomas Ransford, Christophe Reutenauer, Alexander Shnirelman, Stevo Todorcevic, Nicole Tomczak-Jaegermann, and Nick Wormald. —David Eppstein (talk) 08:13, 30 November 2010 (UTC)