Van der Waals equation
This article may be too technical for most readers to understand. (January 2025) |
The van der Waals equation is a mathematical formula that describes the behavior of real gases. It is an equation of state that relates the pressure, temperature, and molar volume in a fluid. The equation modifies the ideal gas law in two ways: first, it considers particles to have a finite diameter (whereas an ideal gas consists of point particles); second, its particles interact with each other (unlike an ideal gas, whose particles move as though alone in the volume).
The equation is named after Dutch physicist Johannes Diderik van der Waals, who first derived it in 1873 as part of his doctoral thesis. Van der Waals based the equation on the idea that fluids are composed of discrete particles, which few scientists believed existed. However, the equation accurately predicted the behavior of a fluid around its critical point, which had been discovered a few years earlier. Its qualitative and quantitative agreement with experiments ultimately cemented its acceptance in the scientific community. These accomplishments won van der Waals the 1910 Nobel Prize in Physics.[1] Today the equation is recognized as an important model of phase change processes.[2] Van der Waals also adapted his equation so that it applied to a binary mixture of fluids. He, and others, then used the modified equation to discover a host of important facts about the phase equilibria of such fluids.[3] This application, expanded to treat multi-component mixtures, has extended the predictive ability of the equation to fluids of industrial and commercial importance. In this arena it has spawned many similar equations in a continuing attempt by engineers to improve their ability to understand and manage these fluids;[4] it remains relevant to the present.[5]
Behavior of the equation
[edit]One way to write the van der Waals equation is:[6][7][8]where is pressure, is the universal gas constant, is temperature, is molar volume, and and are experimentally determinable, substance-specific constants. Molar volume is given by , where is the Avogadro constant, is the volume, and is the number of molecules (the ratio is the amount of substance, a physical quantity with the base unit mole).
When van der Waals created his equation, few scientists believed that fluids were composed of rapidly moving particles. Moreover, those who thought so had no knowledge of the atomic/molecular structure. The simplest conception of a particle, and the easiest to model mathematically, was a hard sphere; this is what van der Waals used. In that case, two particles of diameter would come into contact when their centers were a distance apart; hence the center of the one was excluded from a spherical volume equal to about the other. That is 8 times , the volume of each particle of radius , but there are 2 particles which gives 4 times the volume per particle. The total excluded volume is then ; that is, 4 times the volume of all the particles. Van der Waals and his contemporaries used an alternative, but equivalent, analysis based on the mean free path between molecular collisions that gave this result.[9][10] From the fact that the volume fraction of particles, must be positive, van der Waals noted that as becomes larger the factor 4 must decrease (for spheres there is a known minimum ), but he was never able to determine the nature of the decrease.[11][12]
The constant , and has dimension of molar volume, [v]. The constant expresses the strength of the hypothesized interparticle attraction. Van der Waals only had as a model Newton's law of gravitation, in which two particles are attracted in proportion to the product of their masses. Thus he argued that in his case the attractive pressure was proportional to the square of the density.[13] The proportionality constant, , when written in the form used above, has the dimension [pv2] (pressure times molar volume squared), which is also molar energy times molar volume.

The intermolecular force was later conveniently described by the negative derivative of a pair potential function. For spherically symmetric particles, this is most simply a function of separation distance with a single characteristic length, , and a minimum energy, (with ). Two of the many such functions that have been suggested are shown in the accompanying plot.[15]
A modern theory based on statistical mechanics produces the same result for obtained by van der Waals and his contemporaries. This result is valid for any pair potential for which the increase in is sufficiently rapid. This includes the hard sphere model for which the increase is infinitely rapid and the result is exact. Indeed, the Sutherland potential most accurately models van der Waals' conception of a molecule. It also includes potentials that do not represent hard sphere force interactions provided that the increase in for is fast enough, but then it is approximate; increasingly better the faster the increase. In that case is only an "effective diameter" of the molecule. This theory also produces where is a number that depends on the shape of the potential function, . However, this result is only valid when the potential is weak, namely, when the minimum potential energy is very much smaller than the thermal energy, .[16][17]
In his book (see references [8] and [9]) Ludwig Boltzmann wrote equations using (specific volume) rather than (molar volume, used here); Josiah Willard Gibbs did as well, as do most engineers. Physicists use the property (the reciprocal of number density), but there is no essential difference between equations written with any of these properties. Equations of state written using molar volume contain , those using specific volume contain (the substance specific is the molar mass with the mass of a single particle), and those written with number density contain .
Once the constants and are experimentally determined for a given substance, the van der Waals equation can be used to predict attributes like the boiling point at any given pressure, and the critical point (defined by pressure and temperature such that the substance cannot be liquefied either when no matter how low the temperature, or when no matter how high the pressure; uniquely define ). These predictions are accurate for only a few substances. For most simple fluids they are only a valuable approximation. The equation also explains why superheated liquids can exist above their boiling point and subcooled vapors can exist below their condensation point.

Example
[edit]The graph on the right plots the intersection of the surface shown in Figures A and C and four planes of constant pressure. Each intersection produces a curve in the plane corresponding to the value of the pressure chosen. These curves are isobars, since they represent all the points with the same pressure.
On the red isobar, , the slope is positive over the entire range, (although the plot only shows a finite region). This describes a fluid as homogeneous for all —that is, it does not undergo a phase transition at any temperature—which is a characteristic of all supercritical isobars .
The orange isobar, , is the critical one that marks the boundary between homogeneity and heterogeneity. The critical point lies on this isobar.
The green isobar, , has a region of negative slope. This region consists of states that are unstable and therefore never observed (for this reason this region is shown dotted gray). The green curve thus consists of two disconnected branches, indicated two phase states: a vapor on the right, and a denser liquid on the left.[18] For this pressure, at a temperature (specified by mechanical, thermal, and material equilibrium), the boiling (saturated) liquid and condensing (saturated) vapor coexist, shown on the curve as the left and right green circles, respectively. The locus of these coexistent saturation points across all subcritical isobars forms the saturation curve on the surface. In this situation, the denser liquid will separate and collect below the vapor due to gravity, and a meniscus will form between them. This heterogeneous combination of coexisting liquid and vapor is the phase transition. Heating the liquid in this state increases the fraction of vapor in the mixture—its , an average of and weighted by this fraction, increases while remains the same. This is shown as the horizontal dotted gray line, which represents not a solution of the equation but the observed behavior. The points above , superheated liquid, and those below it, subcooled vapor, are metastable; a sufficiently strong disturbance causes them to transform to the stable alternative. These metastable regions are shown with green dashed lines. In summary, this isobar describes a fluid as a stable vapor for , a stable liquid for , and a mixture of liquid and vapor at , that also supports metastable states of subcooled vapor and superheated liquid. This behavior is characteristic of all subcritical isobars , where is a function of .[19]
The black isobar, , is the limit of positive pressures. None of its points represent stable solutions: they are either metastable (positive or zero slope) or unstable (negative slope). Interestingly, states of negative pressure (tension) exist. Their isobars lie below the black isobar, and form those parts of the surfaces seen in Figures A and C that lie below the zero-pressure plane. In this plane they have a parabola-like shape, and, like the zero-pressure isobar, their states are all either metastable (positive or zero slope) or unstable (negative slope).
Surface plots
[edit]
Figure B shows the surface calculated from the ideal gas equation of state. This surface is universal, meaning it represents all ideal gases. Here, the surface is normalized so that the coordinate is at in the 3-dimensional plot space (the black dot). This normalization makes it easier to compare this surface with the surface generated by the van der Waals equation in Figure C.[20]
Figures A and C show the surface calculated from the van der Waals equation. Note that whereas the ideal gas surface is relatively uniform, the van der Waals surface has a distinctive "fold". This fold develops from a critical point defined by specific values of pressure, temperature, and molar volume. Because the surface is plotted using dimensionless variables (formed by the ratio of each property to its respective critical value), the critical point is located at the coordinates . When drawn using these dimensionless axes, this surface is, like that of the ideal gas, also universal. Moreover, it represents all real substances to a remarkably high degree of accuracy. This principle of corresponding states, developed by van der Waals from his equation, has become one of the fundamental ideas in the thermodynamics of fluids.
The fold's boundary on the surface is marked, on each side of the critical point, by the spinodal curve (identified in Fig. A, and seen in Figs. A and C). This curve delimits an unstable region wherein no observable homogeneous states exist; elsewhere on the surface, states of liquid, vapor, and gas exist. The fold in the surface is what enables the equation to predict the phenomenon of liquid–vapor phase change. This phenomenon is described by the saturation curve (or coexistence curve): the locus of saturated liquid and vapor states which, being in equilibrium with each other, can coexist. The saturation curve is not specified by the properties of the surface alone—it is substance-dependent. The saturated liquid curve and saturated vapor curve (both identified in Fig. A) together comprise the saturation curve. The inset in Figure A shows the mixture states, which are a combination of the saturated liquid and vapor states that correspond to each end of the horizontal mixture line (that is, the points of intersection between the mixture line and its isotherm). However, these mixture states are not part of the surface generated by the van der Waals equation; they are not solutions of the equation.
Relationship to the ideal gas law
[edit]The ideal gas law follows from the van der Waals equation whenever the molar volume is sufficiently large (when , so ), or correspondingly whenever the molar density, , is sufficiently small (when , so ).[21]
When is large enough that both inequalities are satisfied, these two approximations reduce the van der Waals equation to ; rearranging in terms of and gives , which is the ideal gas law.[21] This is not surprising since the van der Waals equation was constructed from the ideal gas equation in order to obtain an equation valid beyond the limit of ideal gas behavior.
What is truly remarkable is the extent to which van der Waals succeeded. Indeed, Epstein in his classic thermodynamics textbook began his discussion of the van der Waals equation by writing, "In spite of its simplicity, it comprehends both the gaseous and the liquid state and brings out, in a most remarkable way, all the phenomena pertaining to the continuity of these two states".[21] Also, in Volume 5 of his Lectures on Theoretical Physics, Sommerfeld, in addition to noting that "Boltzmann[22] described van der Waals as the Newton of real gases",[23] also wrote "It is very remarkable that the theory due to van der Waals is in a position to predict, at least qualitatively, the unstable [referring to superheated liquid, and subcooled vapor, now called metastable] states" that are associated with the phase change process.[24]
Utility of the equation
[edit]The van der Waals equation has been, and remains, useful because:[25]
- It yields simple analytic expressions for thermodynamic properties: internal energy, entropy, enthalpy, Helmholtz free energy, Gibbs free energy, and specific heat at constant pressure .
- It yields an analytic expression of its coefficient of thermal expansion and its isothermal compressibility.
- It yields an analytic analysis of the Joule–Thomson coefficient and associated inversion curve, which were instrumental in the development of the commercial liquefaction of gases.
- It shows that the specific heat at constant volume is a function of only.
- It explains the existence of the critical point and the liquid–vapor phase transition, including the observed metastable states.
- It establishes the theorem of corresponding states.
- It is an intermediate mathematical model, useful as a pedagogical tool when teaching physics, chemistry, and engineering.
In addition, its saturation curve has an analytic solution, which can depict the liquid metals (mercury and cesium) quantitatively, and describes most real fluids qualitatively.[26] As such, this solution can be regarded as one member of a family of equations of state (known as extended corresponding states).[27] Consequently, the equation plays an important role in the modern theory of phase transitions.[28]
History
[edit]In 1857 Rudolf Clausius published The Nature of the Motion which We Call Heat. In it he derived the relation for the pressure in a gas, composed of particles in motion, with number density , mass , and mean square speed . He then noted that using the classical laws of Boyle and Charles, one could write with a constant of proportionality . Hence temperature was proportional to the average kinetic energy of the particles.[29] This article inspired further work based on the twin ideas that substances are composed of indivisible particles, and that heat is a consequence of the particle motion; movement that evolves in accordance with Newton's laws. The work, known as the kinetic theory of gases, was done principally by Clausius, James Clerk Maxwell, and Ludwig Boltzmann. At about the same time, Josiah Willard Gibbs advanced the work by converting it into statistical mechanics.[30][31]

This environment influenced Johannes Diderik van der Waals. After initially pursuing a teaching credential, he was accepted for doctoral studies at the University of Leiden under Pieter Rijke. This led, in 1873, to a dissertation that provided a simple, particle-based equation that described the gas–liquid change of state, the origin of a critical temperature, and the concept of corresponding states.[32][33] The equation is based on two premises: first, that fluids are composed of particles with non-zero volumes, and second, that at a large enough distance each particle exerts an attractive force on all other particles in its vicinity. Boltzmann called these forces van der Waals cohesive forces.[34]
In 1869 Irish professor of chemistry Thomas Andrews at Queen's University Belfast, in a paper entitled On the Continuity of the Gaseous and Liquid States of Matter,[35] displayed an experimentally obtained set of isotherms of carbonic acid, H2CO3, that showed at low temperatures a jump in density at a certain pressure, while at higher temperatures there was no abrupt change (the figure can be seen here). Andrews called the isotherm at which the jump just disappears the critical point. Given the similarity of the titles of this paper and van der Waals' subsequent thesis, one might think that van der Waals set out to develop a theoretical explanation of Andrews' experiments; however, this is not what happened. Van der Waals began work by trying to determine a molecular attraction that appeared in Laplace's theory of capillarity, and only after establishing his equation he tested it using Andrews' results.[36][37]
By 1877 sprays of both liquid oxygen and liquid nitrogen had been produced, and a new field of research, low temperature physics, had been opened. The van der Waals equation played a part in all this, especially with respect to the liquefaction of hydrogen and helium which was finally achieved in 1908.[38] From measurements of and in two states with the same density, the van der Waals equation produces the values[39]
Thus from two such measurements of pressure and temperature one could determine and , and from these values calculate the expected critical pressure, temperature, and molar volume. Goodstein summarized this contribution of the van der Waals equation as follows:[40]
All this labor required considerable faith in the belief that gas–liquid systems were all basically the same, even if no one had ever seen the liquid phase. This faith arose out of the repeated success of the van der Waals theory, which is essentially a universal equation of state, independent of the details of any particular substance once it has been properly scaled. [...] As a result, not only was it possible to believe that hydrogen could be liquefied, but it was even possible to predict the necessary temperature and pressure.
Van der Waals was awarded the Nobel Prize in 1910, in recognition of the contribution of his formulation of this "equation of state for gases and liquids".
As noted previously, modern-day studies of first-order phase changes make use of the van der Waals equation together with the Gibbs criterion, equal chemical potential of each phase, as a model of the phenomenon. This model has an analytic coexistence (saturation) curve expressed parametrically, (the parameter is related to the entropy difference between the two phases), that was first obtained by Plank,[41] was known to Gibbs and others, and was later derived in a beautifully simple and elegant manner by Lekner.[42] A summary of Lekner's solution is presented in a subsequent section, and a more complete discussion in the Maxwell construction.
Critical point and corresponding states
[edit]
Figure 1 shows four isotherms of the van der Waals equation (abbreviated as vdW) on a (pressure, molar volume) plane. The essential character of these curves is that they come in three forms:
- At some critical temperature (orange isotherm), the slope is negative everywhere except at a single inflection point: the critical point , where both the slope and curvature are zero, .
- At higher temperatures (red isotherm), the isotherm's slope is negative everywhere. (This corresponds to values of for which the vdW equation has one real root for ).
- At lower temperatures (green and blue isotherms), all isotherms have two points where the slope is zero. (This corresponds to values of , for which the vdW equation has three real roots for ).
The critical point can be analytically determined by evaluating the two partial derivatives of the vdW equation in (1) and equating them to zero. This produces the critical values and ; plugging these back into the vdW equation gives .[43]
This calculation can also be done algebraically by noting that the vdW equation can be written as a cubic in terms of , which at the critical point is
which, by dividing out , can be refactored as
Separately, since all three roots coalesce at the critical point, we can write
These two cubic equations are the same when all their coefficients are equal; matching like terms produces a system of three equations:
whose solution produces the previous results for .[44][45]
Using these critical values to define reduced (dimensionless) variables , , and renders the vdW equation in the dimensionless form (used to construct Fig. 1):
This dimensionless form is a similarity relation; it indicates that all vdW fluids at the same will plot on the same curve. It expresses the law of corresponding states which Boltzmann described as follows:[46]
All the constants characterizing the gas have dropped out of this equation. If one bases measurements on the van der Waals units [Boltzmann's name for the reduced quantities here], then he obtains the same equation of state for all gases. [...] Only the values of the critical volume, pressure, and temperature depend on the nature of the particular substance; the numbers that express the actual volume, pressure, and temperature as multiples of the critical values satisfy the same equation for all substances. In other words, the same equation relates the reduced volume, reduced pressure, and reduced temperature for all substances.
Obviously such a broad general relation is unlikely to be correct; nevertheless, the fact that one can obtain from it an essentially correct description of actual phenomena is very remarkable.
This "law" is just a special case of dimensional analysis in which an equation containing 6 dimensional quantities, , and 3 independent dimensions, [p], [v], [T] (independent means that "none of the dimensions of these quantities can be represented as a product of powers of the dimensions of the remaining quantities",[47] and [R]=[pv/T]), must be expressible in terms of 6 − 3 = 3 dimensionless groups.[48] Here is a characteristic molar volume, a characteristic pressure, and a characteristic temperature, and the 3 dimensionless groups are . According to dimensional analysis the equation must then have the form , a general similarity relation. In his discussion of the vdW equation, Sommerfeld also mentioned this point.[49] The reduced properties defined previously are , , and . Recent research has suggested that there is a family of equations of state that depend on an additional dimensionless group, and this provides a more exact correlation of properties. Nevertheless, as Boltzmann observed, the van der Waals equation provides an essentially correct description.
The vdW equation produces the critical compressibility factor , while for most real fluids .[50] Thus most real fluids do not satisfy this condition, and consequently their behavior is only described qualitatively by the vdW equation. However, the vdW equation of state is a member of a family of state equations based on the Pitzer (acentric) factor, , and the liquid metals (mercury and cesium) are well approximated by it.[26][51]
Thermodynamic properties
[edit]The properties of molar internal energy and entropy —defined by the first and second laws of thermodynamics, hence all thermodynamic properties of a simple compressible substance—can be specified, up to a constant of integration, by two measurable functions: a mechanical equation of state , and a constant volume specific heat .
Internal energy and specific heat at constant volume
[edit]The internal energy is given by the energetic equation of state,[52][53]
where is an arbitrary constant of integration.
Now in order for to be an exact differential—namely that be continuous with continuous partial derivatives—its second mixed partial derivatives must also be equal, . Then with this condition can be written as . Differentiating for the vdW equation gives , so . Consequently for a vdW fluid exactly as it is for an ideal gas. For simplicity, it is regarded as a constant here, for some constant number . Then both integrals can be evaluated, resulting in
| 2 |
This is the energetic equation of state for a perfect vdW fluid. By making a dimensional analysis (what might be called extending the principle of corresponding states to other thermodynamic properties) it can be written in the reduced form[54]
where and is a dimensionless constant.
Enthalpy
[edit]The enthalpy of a system is given by . Substituting with Eq. 2 and (the vdW equation multiplied by ) gives
This is the enthalpic equation of state for a perfect vdW fluid, or in reduced form,[55]
Entropy
[edit]The entropy is given by the entropic equation of state:[56][53]
Using as before, and integrating the second term using we obtain
This is the entropic equation of state for a perfect vdW fluid, or in reduced form,[55]
Helmholtz free energy
[edit]The Helmholtz free energy is , so combining the previous results gives
This is the Helmholtz free energy for a perfect vdW fluid, or in reduced form,
Gibbs free energy
[edit]The Gibbs free energy is , so combining the previous results gives
| 3 |
This is the Gibbs free energy for a perfect vdW fluid, or in reduced form,
Thermodynamic derivatives: α, κT and cp
[edit]The two first partial derivatives of the vdW equation are
where is the isothermal compressibility (a measure of the relative increase of volume from an increase of pressure, at constant temperature), and is the coefficient of thermal expansion (a measure of the relative increase of volume from an increase of temperature, at constant pressure). Therefore,[57][55]
| 4 |
In the limit , the vdW equation becomes , and , and . Both these limits of and are the ideal gas values, which is consistent because, as noted earlier, a vdW fluid behaves like an ideal gas in this limit.
The specific heat at constant pressure is defined as the partial derivative . However, it is not independent of , as they are related by the Mayer equation, .[58][59][60] Then the two partials of the vdW equation can be used to express as[61]
Here in the limit , , which is also the ideal gas result as expected;[61] however the limit gives the same result, which does not agree with experiments on liquids.
In this liquid limit we also find , namely that the vdW liquid is incompressible. Moreover, since , it is also mechanically incompressible, that is, approaches 0 faster than does.
Finally, , , and are all infinite on the curve .[61] This curve, called the spinodal curve, is defined by .
Stability
[edit]According to the extremum principle of thermodynamics, and ; namely, that at equilibrium the entropy is a maximum. This leads to a requirement that .[62] This mathematical criterion expresses a physical condition which Epstein described as follows:[21]
It is obvious that this middle part, dotted in our curves [the place where the requirement is violated, dashed gray in Fig. 1], can have no physical reality. In fact, let us imagine the fluid in a state corresponding to this part of the curve contained in a heat conducting vertical cylinder whose top is formed by a piston. The piston can slide up and down in the cylinder, and we put on it a load exactly balancing the pressure of the gas. If we take a little weight off the piston, there will no longer be equilibrium and it will begin to move upward. However, as it moves the volume of the gas increases and with it its pressure. The resultant force on the piston gets larger, retaining its upward direction. The piston will, therefore, continue to move and the gas to expand until it reaches the state represented by the maximum of the isotherm. Vice versa, if we add ever so little to the load of the balanced piston, the gas will collapse to the state corresponding to the minimum of the isotherm.

For isotherms , this requirement is satisfied everywhere, thus all states are gas. For isotherms , the states that lie between the local minimum and local maximum , for which (shown dashed gray in Fig. 1), are unstable and thus not observed. This unstable region is the genesis of the phase change; there is a range , for which no observable states exist. The states for are liquid, and those for are vapor; the denser liquid separates and lies below the vapor due to gravity. The transition points, states with zero slope, are called spinodal points.[63] Their locus is the spinodal curve, a boundary that separates the regions of the plane for which liquid, vapor, and gas exist from a region where no observable homogeneous states exist. This spinodal curve is obtained here from the vdW equation by differentiation (or equivalently from ) as
A projection of the spinodal curve is plotted in Figure 1 as the black dash-dot curve. It passes through the critical point, which is also a spinodal point.
Saturation
[edit]Although the gap in delimited by the two spinodal points on an isotherm (e.g. in Fig. 1) is the origin of the phase change, the change occurs as some intermediate value. This can be seen by considering that both saturated liquid and saturated vapor can coexist in equilibrium, at which they have the same pressure and temperature.[64] However, the minimum and maximum spinodal points are not at the same pressure. Therefore, at a temperature , the phase change is characterized by the pressure , which lies within the range of set by the spinodal points (), and by the molar volume of liquid and vapor , which lie outside the range of set by the spinodal points ( and ).
Applying the vdW equation to the saturated liquid (fluid) and saturated vapor (gas) states gives:
| 5 |
These two equations contain four variables (), so a third equation is required in order to uniquely specify three of these variables in terms of the fourth. The following is a derivation of this third equation (the result is Eq. 6).
Now, the energy required to vaporize a mole at constant pressure is (from the first law of thermodynamics) and at constant temperature is (from the second law). Thus,
That is, in this case, the Gibbs free energy in the saturated liquid state equals that in the saturated vapor state.[65] The Gibbs free energy is one of the four thermodynamic potentials whose partial derivatives produce all other thermodynamics state properties;[66] its differential is . Integrating this over an isotherm from to , noting that the pressure is the same at each endpoint, and setting the result to zero yields
Here because is a multivalued function, the integral must be divided into 3 parts corresponding to the 3 real roots of the vdW equation in the form, (this can be visualized most easily by imagining Fig. 1 rotated ); the result is a special case of material equilibrium.[67] The last equality, which follows from integrating , is the Maxwell equal area rule, which requires that the upper area between the vdW curve and the horizontal through be equal to the lower area.[68] This form means that the thermodynamic restriction that fixes is specified by the equation of state itself, . Using the equation for the Gibbs free energy for the vdW equation (Eq. 3), the difference can be evaluated as
| 6 |
This is a third equation that along with the two vdW equations of Eqs. 5 can be solved numerically. This has been done given a value for either or , and tabular results presented;[69][70] however, the equations also admit an analytic parametric solution obtained most simply and elegantly, by Lekner.[42] Details of this solution may be found in the Maxwell construction; the results are:
where
and the parameter is given physically by . The values of all other property discontinuities across the saturation curve also follow from this solution.[71] These functions define the coexistence curve (or saturation curve), which is the locus of the saturated liquid and saturated vapor states of the vdW fluid. Various projections of this saturation curve are plotted in Figures 1, 2a, and 2b.

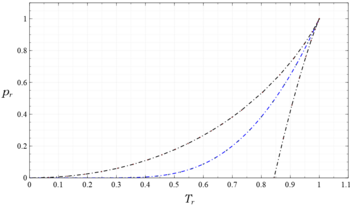
Referring back to Figure 1, the isotherms for are discontinuous. For example, the (green) isotherm consists of two separate segments. The solid green lines represent stable states, and terminate at dots that represent the saturated liquid and vapor states that comprise the phase change. The dashed green lines represent metastable states (superheated liquid and subcooled vapor) that are created in the process of phase transition, have a short lifetime, and then devolve into their lower energy stable alternative.
At every point in the region between the two curves in Figure 2b, there are two states: one stable and one metastable. The coexistence of these states can be seen in Figure 1—for discontinuous isotherms, there are values of which correspond to two points on the isotherm: one on a solid line (the stable state) and one on a dashed region (the metastable state).
In his treatise of 1898, in which he described the van der Waals equation in great detail, Boltzmann discussed these metastable states in a section titled "Undercooling, Delayed evaporation".[72] (Today, these states are now denoted "subcooled vapor" and "superheated liquid".) Moreover, it has now become clear that these metastable states occur regularly in the phase transition process. In particular, processes that involve very high heat fluxes create large numbers of these states, and transition to their stable alternative with a corresponding release of energy that can be dangerous. Consequently, there is a pressing need to study their thermal properties.[73]
In the same section, Boltzmann also addressed and explained the negative pressures which some liquid metastable states exhibit (for example, the blue isotherm in Fig. 1). He concluded that such liquid states of tensile stresses were real, as did Tien and Lienhard many years later who wrote "The van der Waals equation predicts that at low temperatures liquids sustain enormous tension [...] In recent years measurements have been made that reveal this to be entirely correct."[74]
Even though the phase change produces a mathematical discontinuity in the homogeneous fluid properties (for example ), there is no physical discontinuity.[67] As the liquid begins to vaporize, the fluid becomes a heterogeneous mixture of liquid and vapor whose molar volume varies continuously from to according to the equation of state where and is the mole fraction of the vapor. This equation is called the lever rule and applies to other properties as well.[24][67] The states it represents form a horizontal line bridging the discontinuous region of an isotherm (not shown in Fig. 1 because it is a different equation from the vdW equation).
Extended corresponding states
[edit]
The idea of corresponding states originated when van der Waals cast his equation in the dimensionless form, . However, as Boltzmann noted, such a simple representation could not correctly describe all substances. Indeed, the saturation analysis of this form produces ; namely, that all substances have the same dimensionless coexistence curve, which is not true.[75] To avoid this paradox, an extended principle of corresponding states has been suggested in which where is a substance-dependent dimensionless parameter related to the only physical feature associated with an individual substance: its critical point.

One candidate for is the critical compressibility factor ; however, because is difficult to measure accurately, the acentric factor developed by Kenneth Pitzer,[76] , is more useful. The saturation pressure in this situation is represented by a one-parameter family of curves: . Several investigators have produced correlations of saturation data for a number of substances; Dong and Lienhard give[51]
which has an RMS error of over the range .
Figure 3 is a plot of vs for various values of the Pitzer factor as given by this equation. The vertical axis is logarithmic in order to show the behavior at pressures closer to zero, where differences among the various substances (indicated by varying values of ) are more pronounced.
Figure 4 is another plot of the same equation showing as a function of for various values of . It includes data from 51 substances, including the vdW fluid, over the range . This plot shows that the vdW fluid () is a member of the class of real fluids; indeed, the vdW fluid can quantitatively approximate the behavior of the liquid metals cesium () and mercury (), which share similar values of . However, in general it can describe the behavior of fluids of various only qualitatively.
Joule–Thomson coefficient
[edit]The Joule–Thomson coefficient, , is of practical importance because the two end states of a throttling process () lie on a constant enthalpy curve. Although ideal gases, for which , do not change temperature in such a process, real gases do, and it is important in applications to know whether they heat up or cool down.[77]
This coefficient can be found in terms of the previously derived and as[78]
When is positive, the gas temperature decreases as it passes through a throttling process, and when it is negative, the temperature increases. Therefore, the condition defines a curve that separates the region of the plane where from the region where . This curve is called the inversion curve, and its equation is . Evaluating this using the expression for derived in Eq. 4 produces
Note that for there will be cooling for (or, in terms of the critical temperature, ). As Sommerfeld noted, "This is the case with air and with most other gases. Air can be cooled at will by repeated expansion and can finally be liquified."[79]

In terms of , the equation has a simple positive solution , which for produces . Using this to eliminate from the vdW equation then gives the inversion curve as
where, for simplicity, have been replaced by .
The maximum of this quadratic curve occurs with , for
which gives , or , and the corresponding . By the quadratic formula, the zeros of the curve are and ( and ). In terms of the dimensionless variables , the zeros are at and , while the maximum is , and occurs at . A plot of the curve is shown in green in Figure 5. Sommerfeld also displays this plot,[80] together with a curve drawn using experimental data from H2. The two curves agree qualitatively, but not quantitatively. For example the maximum on these two curves differ by about 40% in both magnitude and location.[excessive detail?]
Figure 5 shows an overlap between the saturation curve and the inversion curve plotted in the same region. This crossover means a van der Waals gas can be liquified by passing it through a throttling process under the proper conditions; real gases are liquified in this way.
Compressibility factor
[edit]

Real gases are characterized by their difference from ideal gases by writing . Here , called the compressibility factor, is expressed either as or .[clarification needed] In either case, the limit as or approaches zero is 1, and takes the ideal gas value. In the second case ,[81] so for a van der Waals fluid the compressibility factor is
| 7 |
or in terms of reduced variables
where . At the critical point, and .
In the limit , ; the fluid behaves like an ideal gas, as mentioned before. The derivative is never negative when ; that is, when (which corresponds to ). Alternatively, the initial slope is negative when , is zero at , and is positive for larger (see Fig. 6). In this case, the value of passes through when . Here is called the Boyle temperature. It ranges between , and denotes a point in space where the equation of state reduces to the ideal gas law. However, the fluid does not behave like an ideal gas there, because neither its derivatives nor reduce to their ideal gas values, other than where the actual ideal gas region.[82]
Figure 6 plots various isotherms of vs . Also shown are the spinodal and coexistence curves described previously. The subcritical isotherm consists of stable, metastable, and unstable segments (identified in the same way as in Fig. 1). Also included are the zero initial slope isotherm and the one corresponding to infinite temperature.
Figure 7 shows a generalized compressibility chart for a vdW gas. Like all other vdW properties, this is not quantitatively correct for most gases, but it has the correct qualitative features.[83][84] Note the caustic generated by the crossing isotherms.
Virial expansion
[edit]Statistical mechanics suggests that the compressibility factor can be expressed by a power series, called a virial expansion:[85]
where the functions are the virial coefficients; the th term represents a -particle interaction.
Expanding the term in the definition of (Eq. 7) into an infinite series, convergent for , produces
The corresponding expression for when is
These are the virial expansions, one dimensional and one dimensionless, for the van der Waals fluid. The second virial coefficient is the slope of at . Notice that it can be positive when or negative when , which agrees with the result found previously by differentiation.
For molecules modeled as non-attracting hard spheres, , and the vdW virial expansion becomes
which illustrates the effect of the excluded volume alone. It was recognized early on that this was in error beginning with the term . Boltzmann calculated its correct value as , and used the result to propose an enhanced version of the vdW equation:
On expanding , this produced the correct coefficients through and also gave infinite pressure at , which is approximately the close-packing distance for hard spheres.[86] This was one of the first of many equations of state proposed over the years that attempted to make quantitative improvements to the remarkably accurate explanations of real gas behavior produced by the vdW equation.[87]
Mixtures
[edit]In 1890 van der Waals published an article that initiated the study of fluid mixtures. It was subsequently included as Part III of a later published version of his thesis.[88] His essential idea was that in a binary mixture of vdW fluids described by the equations
the mixture is also a vdW fluid given by
where
Here and , with (so that ), are the mole fractions of the two fluid substances. Adding the equations for the two fluids shows that , although for sufficiently large with equality holding in the ideal gas limit. The quadratic forms for and are a consequence of the forces between molecules. This was first shown by Lorentz,[89] and was credited to him by van der Waals. The quantities and in these expressions characterize collisions between two molecules of the same fluid component, while and represent collisions between one molecule of each of the two different fluid components. This idea of van der Waals' was later called a one fluid model of mixture behavior.[90]
Assuming that is the arithmetic mean of and , , substituting into the quadratic form and noting that produces
Van der Waals wrote this relation, but did not make use of it initially.[91] However, it has been used frequently in subsequent studies, and its use is said to produce good agreement with experimental results at high pressure.[92]
Common tangent construction
[edit]In this article, van der Waals used the Helmholtz potential minimum principle to establish the conditions of stability. This principle states that in a system in diathermal contact with a heat reservoir , , and , namely at equilibrium, the Helmholtz potential is a minimum.[93] Since, like , the molar Helmholtz function is also a potential function whose differential is
this minimum principle leads to the stability condition . This condition means that the function, , is convex at all stable states of the system. Moreover, for those states the previous stability condition for the pressure is necessarily satisfied as well.
Single fluid
[edit]For a single substance, the definition of the molar Gibbs free energy can be written in the form . Thus when and are constant along with temperature, the function represents a straight line with slope , and intercept . Since the curve has positive curvature everywhere when , the curve and the straight line will have a single tangent. However, for a subcritical is not everywhere convex. With and a suitable value of , the line will be tangent to at the molar volume of each coexisting phase: saturated liquid and saturated vapor ; there will be a double tangent. Furthermore, each of these points is characterized by the same values of , , and These are the same three specifications for coexistence that were used previously.

Figure 8 depicts an evaluation of as a green curve, with and marked by the left and right green circles, respectively. The region on the green curve for corresponds to the liquid state. As increases past , the curvature of (proportional to ) continually decreases. The inflection point, characterized by zero curvature, is a spinodal point; between and this point is the metastable superheated liquid. For further increases in the curvature decreases to a minimum then increases to another (zero curvature) spinodal point; between these two spinodal points is the unstable region in which the fluid cannot exist in a homogeneous equilibrium state (represented by the dotted grey curve). With a further increase in the curvature increases to a maximum at , where the slope is ; the region between this point and the second spinodal point is the metastable subcooled vapor. Finally, the region is the vapor. In this region the curvature continually decreases until it is zero at infinitely large . The double tangent line (solid black) that runs between and represents states that are stable but heterogeneous, not homogeneous solutions of the vdW equation.[94] The states above this line (with larger Helmholtz free energy) are either metastable or unstable.[94] The combined solid green-black curve in Figure 8 is the convex envelope of , which is defined as the largest convex curve that is less than or equal to the function.[95]
For a vdW fluid, the molar Helmholtz potential is
where . Its derivative is
which is the vdW equation, as expected. A plot of this function , whose slope at each point is specified by the vdW equation, for the subcritical isotherm is shown in Figure 8 along with the line tangent to it at its two coexisting saturation points. The data illustrated in Figure 8 is exactly the same as that shown in Figure 1 for this isotherm. This double tangent construction thus provides a graphical alternative to the Maxwell construction to establish the saturated liquid and vapor points on an isotherm.
Binary fluid
[edit]Van der Waals used the Helmholtz function because its properties could be easily extended to the binary fluid situation. In a binary mixture of vdW fluids, the Helmholtz potential is a function of two variables, , where is a composition variable (for example so ). In this case, there are three stability conditions:
and the Helmholtz potential is a surface (of physical interest in the region ). The first two stability conditions show that the curvature in each of the directions and are both non-negative for stable states, while the third condition indicates that stable states correspond to elliptic points on this surface.[96] Moreover, its limit
specifies the spinodal curves on the surface.
For a binary mixture, the Euler equation[97] can be written in the form
where are the molar chemical potentials of each substance, . For constant values of , , and , this equation is a plane with slopes in the direction, in the direction, and intercept . As in the case of a single substance, here the plane and the surface can have a double tangent, and the locus of the coexisting phase points forms a curve on each surface. The coexistence conditions are that the two phases have the same , , , and ; the last two are equivalent to having the same and individually, which are just the Gibbs conditions for material equilibrium in this situation. The two methods of producing the coexistence surface are equivalent.
Although this case is similar to that of a single fluid, here the geometry can be much more complex. The surface can develop a wave (called a plait or fold) in the direction as well as the one in the direction. Therefore, there can be two liquid phases that can be either miscible, or wholly or partially immiscible, as well as a vapor phase.[98][99] Despite a great deal of both theoretical and experimental work on this problem by van der Waals and his successors—work which produced much useful knowledge about the various types of phase equilibria that are possible in fluid mixtures[100]—complete solutions to the problem were only obtained after 1967, when the availability of modern computers made calculations of mathematical problems of this complexity feasible for the first time.[101] The results obtained were, in Rowlinson's words,
a spectacular vindication of the essential physical correctness of the ideas behind the van der Waals equation, for almost every kind of critical behavior found in practice can be reproduced by the calculations, and the range of parameters that correlate with the different kinds of behavior are intelligible in terms of the expected effects of size and energy.[102]
Mixing rules
[edit]In order to obtain these numerical results, the values of the constants of the individual component fluids must be known. In addition, the effect of collisions between molecules of the different components, given by and , must also be specified. In the absence of experimental data, or computer modeling results to estimate their value the empirical combining rules, geometric and algebraic means can be used, respectively:[103]
These relations correspond to the empirical combining rules for the intermolecular force constants,
the first of which follows from a simple interpretation of the dispersion forces in terms of polarizabilities of the individual molecules, while the second is exact for rigid molecules.[104] Using these empirical combining rules to generalize for fluid components, the quadradic mixing rules for the material constants are:[92]
These expressions come into use when mixing gases in proportion, such as when producing tanks of air for diving[105] and managing the behavior of fluid mixtures in engineering applications. However, more sophisticated mixing rules are often necessary, in order to obtain satisfactory agreement with reality over the wide variety of mixtures encountered in practice.[106][107]
Another method of specifying the vdW constants, pioneered by W.B. Kay and known as Kay's rule,[108] specifies the effective critical temperature and pressure of the fluid mixture by
In terms of these quantities, the vdW mixture constants are
which Kay used as the basis for calculations of the thermodynamic properties of mixtures.[109] Kay's idea was adopted by T. W. Leland, who applied it to the molecular parameters , which are related to through by and . Using these together with the quadratic mixing rules for produces
which is the van der Waals approximation expressed in terms of the intermolecular constants.[110][111] This approximation, when compared with computer simulations for mixtures, are in good agreement over the range , namely for molecules of similar diameters. In fact, Rowlinson said of this approximation, "It was, and indeed still is, hard to improve on the original van der Waals recipe when expressed in [this] form".[112]
Mathematical and empirical validity
[edit]Since van der Waals presented his thesis, "[m]any derivations, pseudo-derivations, and plausibility arguments have been given" for it.[113] However, no mathematically rigorous derivation of the equation over its entire range of molar volume that begins from a statistical mechanical principle exists. Indeed, such a proof is not possible, even for hard spheres.[114][115][116] Goodstein put it this way, "Obviously the value of the van der Waals equation rests principally on its empirical behavior rather than its theoretical foundation."[117]
Nevertheless, a review of the work that has been done is useful in order to better understand where and when the equation is valid mathematically, and where and why it fails.
Review
[edit]The classical canonical partition function, , of statistical mechanics for a three dimensional particle macroscopic system is
| 8 |
where , is the de Broglie wavelength (alternatively is the quantum concentration), is the particle configuration integral, and is the intermolecular potential energy, which is a function of the particle position vectors . Lastly is the volume element of , which is a -dimensional space.[118][119][120][121]
The connection of with thermodynamics is made through the Helmholtz free energy, , from which all other properties can be found; in particular . For point particles that have no force interactions (), all integrals of can be evaluated producing . In the thermodynamic limit, with finite, the Helmholtz free energy per particle (or per mole, or per unit mass) is finite; for example, per mole it is . The thermodynamic state equations in this case are those of a monatomic ideal gas, specifically [122]
Early derivations of the vdW equation were criticized mainly on two grounds.[123] First, a rigorous derivation from the partition function should produce an equation that does not include unstable states for which, . Second, the constant in the vdW equation (here is the volume of a single molecule) gives the maximum possible number of molecules as , or a close packing density of 1/4=0.25, whereas the known close-packing density of spheres is .[124] Thus a single value of cannot describe both gas and liquid states.
The second criticism is an indication that the vdW equation cannot be valid over the entire range of molar volume. Van der Waals was well aware of this problem; he devoted about 30% of his Nobel lecture to it, and also said that it is[125]
... the weak point in the study of the equation of state. I still wonder whether there is a better way. In fact this question continually obsesses me, I can never free myself from it, it is with me even in my dreams.
In 1949 the first criticism was proved by van Hove when he showed that in the thermodynamic limit, hard spheres with finite-range attractive forces have a finite Helmholtz free energy per particle. Furthermore, this free energy is a continuously decreasing function of the volume per particle (see Fig. 8 where are molar quantities). In addition, its derivative exists and defines the pressure, which is a non-increasing function of the volume per particle.[126] Since the vdW equation has states for which the pressure increases with increasing volume per particle, this proof means it cannot be derived from the partition function, without an additional constraint that precludes those states.
In 1891 Korteweg used kinetic theory ideas to show[127] that a system of hard rods of length , constrained to move along a straight line of length and exerting only direct contact forces on one another, satisfy a vdW equation with ; Rayleigh also knew this.[128] Tonks, by evaluating the configuration integral,[129] later showed that the force exerted on a wall by this system is given by with . This can be put in a more recognizable, molar, form by dividing by the rod cross sectional area , and defining . This produces ; there is no condensation, as for all . This result is obtained because in one dimension, particles cannot pass by one another as they can in higher dimensions; their mass center coordinates satisfy the relations . As a result, the configuration integral is .[130]
In 1959 this one-dimensional gas model was extended by Kac to include particle pair interactions through an attractive potential, . This specific form allowed evaluation of the grand partition function,
| 9 |
in the thermodynamic limit, in terms of the eigenfunctions and eigenvalues of a homogeneous integral equation.[131] Although an explicit equation of state was not obtained, it was proved that the pressure was a strictly decreasing function of the volume per particle, hence condensation did not occur.

Four years later, in 1963, Kac together with Uhlenbeck and Hemmer modified the pair potential of Kac's previous work as , so that
was independent of .[132] They found that a second limiting process they called the van der Waals limit, (in which the pair potential becomes both infinitely long range and infinitely weak) and performed after the thermodynamic limit, produced the one-dimensional vdW equation (here rendered in molar form)
as well as the Gibbs criterion, (equivalently the Maxwell construction). As a result, all isotherms satisfy the condition as shown in Figure 9, and hence the first criticism of the vdW equation is not as serious as originally thought.[133]
Then, in 1966, Lebowitz and Penrose generalized what they called the Kac potential, , to apply to a nonspecific function of dimensions:
For and this reduces to the specific one-dimensional function considered by Kac, et al., and for it is an arbitrary function (although subject to specific requirements) in physical three-dimensional space. In fact, the function must be bounded, non-negative, and one whose integral
is finite, independent of .[134][135] By obtaining upper and lower bounds on and hence on , taking the thermodynamic limit ( with finite) to obtain upper and lower bounds on the function , then subsequently taking the van der Waals limit, they found that the two bounds coalesced and thereby produced a unique limit (here written in terms of the free energy per mole and the molar volume):
The abbreviation stands for "convex envelope"; this is a function which is the largest convex function that is less than or equal to the original function. The function is the limit function when ; also here . This result is illustrated in Figure 8 by the solid green curves and black line, which is the convex envelope of .
The corresponding limit for the pressure is a generalized form of the vdW equation
together with the Gibbs criterion, (equivalently the Maxwell construction). Here is the pressure when attractive molecular forces are absent.
The conclusion from all this work is that a rigorous mathematical derivation from the partition function produces a generalization of the vdW equation together with the Gibbs criterion if the attractive force is infinitely weak with an infinitely long range. In that case, , the pressure that results from direct particle collisions (or more accurately the core repulsive forces), replaces . This is consistent with the second criticism, which can be stated as . Consequently, the vdW equation cannot be rigorously derived from the configuration integral over the entire range of .
Nevertheless, it is possible to rigorously show that the vdW equation is equivalent to a two-term approximation of the virial equation. Hence it can be rigorously derived from the partition function as a two-term approximation in the additional limit .
The virial equation of state
[edit]This derivation is simplest when begun from the grand partition function, (Eq. 9).[136]
In this case, the connection with thermodynamics is through , together with the number of particles Substituting the expression for (Eq. 8) in the series for produces
Expanding in its convergent power series, using in each term, and equating powers of produces relations that can be solved for the in terms of the . For example, , , and .
Then from , the number density is expressed as the series
which can be inverted to give
The coefficients are given in terms of by the Lagrange inversion theorem, or determined by substituting into the series for and equating powers of ; thus , and so on. Finally, using this series in the series for produces the virial expansion,[137] or virial equation of state
The second virial coefficient
[edit]This conditionally convergent series is also an asymptotic power series for the limit , and a finite number of terms is an asymptotic approximation to .[138] The dominant order approximation in this limit is , which is the ideal gas law. It can be written as an equality using order symbols,[139] for example , which states that the remaining terms approach zero in the limit (or , which states, more accurately, that they approach zero in proportion to ). The two-term approximation is , and the expression for is

where and is a dimensionless two-particle potential function. For spherically symmetric molecules, this function can be represented most simply with two parameters: a characteristic molecular diameter and a binding energy , as shown in the Figure 10 plot, in which . Also, for spherically symmetric molecules, five of the six integrals in the expression for can be done with the result
From its definition, is positive for , and negative for with a minimum of at some . Furthermore, increases so rapidly that whenever then . In addition, in the limit ( is a dimensionless "coldness", and the quantity is a characteristic molecular temperature), the exponential can be approximated for by two terms of its power series expansion. In these circumstances, can be approximated as
where has the minimum value of . On splitting the interval of integration into two parts, one less than and the other greater than , evaluating the first integral and making the second integration variable dimensionless using produces[140] [141]
where and , where is a numerical factor whose value depends on the specific dimensionless intermolecular-pair potential
Here and , where are the constants given in the introduction. The condition that be finite requires that be integrable over the range . This result indicates that a dimensionless (that is, a function of a dimensionless molecular temperature ) is a universal function for all real gases with an intermolecular pair potential of the form . This is an example of the principle of corresponding states on the molecular level.[142] Moreover, this is true in general and has been developed extensively both theoretically and experimentally.[143][144]
The van der Waals approximation
[edit]Substituting the (approximate in ) expression for into the two-term virial approximation produces
Here the approximation is written in terms of molar quantities; its first two terms are the same as the first two terms of the vdW virial equation.[clarification needed]
The Taylor expansion of , uniformly convergent for , can be written as , so substituting for produces
Alternatively this is
which is the vdW equation.[145]
Summary
[edit]According to this derivation, the vdW equation is an equivalent of the two-term approximation of the virial equation of statistical mechanics in the limits . Consequently the equation produces an accurate approximation in a region defined by (on a molecular basis ), which corresponds to a dilute gas. But as the density increases, the behavior of the vdW approximation and the two-term virial expansion differ markedly. Whereas the virial approximation in this instance either increases or decreases continuously, the vdW approximation together with the Maxwell construction expresses physical reality in the form of a phase change, while also indicating the existence of metastable states. This difference in behaviors was pointed out by Korteweg[146] and Rayleigh (see Rowlinson[147]) in the course of their dispute with Tait about the vdW equation.
In this extended region, use of the vdW equation is not justified mathematically; however, it has empirical validity. Its various applications in this region that attest to this, both qualitative and quantitative, have been described previously in this article. This point was also made by Alder, et al. who, at a conference marking the 100th anniversary of van der Waals' thesis, noted that:[148]
It is doubtful whether we would celebrate the centennial of the Van der Waals equation if it were applicable only under circumstances where it has been proven to be rigorously valid. It is empirically well established that many systems whose molecules have attractive potentials that are neither long-range nor weak conform nearly quantatively to the Van der Waals model. An example is the theoretically much studied system of Argon, where the attractive potential has only a range half as large as the repulsive core.
They continued by saying that this model has "validity down to temperatures below the critical temperature, where the attractive potential is not weak at all but, in fact, comparable to the thermal energy." They also described its application to mixtures "where the Van der Waals model has also been applied with great success. In fact, its success has been so great that not a single other model of the many proposed since, has equalled its quantitative predictions,[149] let alone its simplicity."[150]
Engineers have made extensive use of this empirical validity, modifying the equation in numerous ways (by one account there have been some 400 cubic equations of state produced)[151] in order to manage the liquids,[152] and gases of pure substances and mixtures,[153] that they encounter in practice.
This situation has been aptly described by Boltzmann:[154]
...van der Waals has given us such a valuable tool that it would cost us much trouble to obtain by the subtlest deliberations a formula that would really be more useful than the one that van der Waals found by inspiration, as it were.
Notes
[edit]- ^ van der Waals, (1910)
- ^ Goodstein, pp. 443-463
- ^ DeBoer, pp. 7-16
- ^ Valderrama (2010), pp. 415-420
- ^ Kontogeorgis, et al., pp. 4619-4637
- ^ van der Waals, p. 174.
- ^ Epstein, P.S., p 9
- ^ a b Boltzmann, p 231
- ^ a b van der Waals, pp. 168-172
- ^ Boltzmann, p. 221–224
- ^ van der Waals, p. 172
- ^ van der Waals, (1910) p. 256
- ^ van der Waals, p. 173
- ^ Hirschfelder, et al., pp. 31-34
- ^ Hirschfelder, et al., pp. 31-34
- ^ Goodstein, pp. 250, 263
- ^ Tien, Lienhard, pp. 250, 251
- ^ Truesdell, Bharatha, pp 13–15
- ^ Epstein, p. 11
- ^ Goodstein, pp. 303-304, 316, 452
- ^ a b c d Epstein, p.10
- ^ Boltzmann, L. Enzykl. der Mathem. Wiss., V,(1), 550
- ^ Sommerfeld, p 55
- ^ a b Sommerfeld, p 66
- ^ Sommerfeld, pp. 55–68
- ^ a b Lienhard, pp. 172-173
- ^ Peck, R.E.
- ^ Goodstein, pp 443–452
- ^ Weinberg, S., pp. 4–5
- ^ Weinberg, p. 33
- ^ Gibbs, J.W., pp vii–xii
- ^ van der Waals, J.D., (1873), "Over de Continuïteit van den Gas en Vloeistoftoestand", Leiden, Ph.D. Thesis Leiden Univ
- ^ van der Waals, (1984), pp.121–240
- ^ Boltzmann, p 218
- ^ Andrews, T., (1869), "On the Continuity of the Gaseous and Liquid States of Matter", Philosophical Transactions of the Royal Society of London, 159, 575-590
- ^ Klein, M. J., p. 31
- ^ van der Waals, pp. 125, 191–194
- ^ Goodstein, pp. 450–451
- ^ Boltzmann, pp. 232–233
- ^ Goodstein, p. 452
- ^ van der Waals, Rowlinson (ed.), p. 19
- ^ a b Lekner, pp.161-162
- ^ Sommerfeld, pp. 56–57
- ^ Goodstein, p 449
- ^ Boltzmann, pp 237-238
- ^ Boltzmann, pp 239–240
- ^ Barenblatt, p. 16.
- ^ Barenblatt, pp. 13–23
- ^ Sommerfeld, p. 57
- ^ Johnston, p. 6
- ^ a b Dong and Lienhard, pp. 158-159
- ^ Whitman, p 155
- ^ a b Moran and Shapiro, p 574
- ^ Johnston, p. 10
- ^ a b c Johnston, p. 11
- ^ Whitman, p. 203
- ^ Sommerfeld, p 56
- ^ Whitman, p. 204
- ^ Moran and Shapiro, p. 580
- ^ Johnston, p. 3
- ^ a b c Johnston, p.12
- ^ Callen, pp 131–135
- ^ Lienhard, et al., pp. 297-298
- ^ Callen, pp. 37–44
- ^ Callen, p. 153
- ^ Callen, pp. 85–101
- ^ a b c Callen, pp. 146–156
- ^ Maxwell, pp. 358-359
- ^ Shamsundar and Lienhard, pp. 878,879
- ^ Barrufet,and Eubank, pp. 170
- ^ Johnston, D.C., pp 16-18
- ^ Boltzmann, pp. 248–250
- ^ Lienhard, et al., p 297
- ^ Tien and Lienhard, p.254
- ^ van der Waals, Rowlinson (ed.), p. 22
- ^ Pitzer, K.S., et al., p.3433
- ^ Sommerfeld, pp. 61–63
- ^ Sommerfeld, pp 60-62
- ^ Sommerfeld, p 61
- ^ Sommerfeld, p. 62 Fig.8
- ^ Van Wylen and Sonntag, p. 49
- ^ Johnston, p. 10
- ^ Su, G.J., (1946), "Modified Law of Corresponding States for Real Gases", Ind. Eng. Chem., 38, 803
- ^ Moran, and Shapiro, p. 113
- ^ Tien and Lienhard, pp. 247–248
- ^ Boltzmann, pp. 353-356
- ^ van der Waals, Rowlinson (ed.), pp. 20-22
- ^ van der Waals, pp. 243-282
- ^ Lorentz, H. A., (1881), Ann. der Physik und Chemie, 12, 127, 134, 600
- ^ van der Waals, Rowlinson (ed.), p. 68
- ^ van der Waals, p. 244
- ^ a b Redlich, O.; Kwong, J. N. S. (1949). "On the Thermodynamics of Solutions. V. An Equation of State. Fugacities of Gaseous Solutions" (PDF). Chemical Reviews. 44 (1): 233–244. doi:10.1021/cr60137a013. PMID 18125401. Retrieved 2 April 2024.
- ^ Callen, p. 105
- ^ a b van der Waals, pp. 245-247
- ^ Lebowitz, p. 52
- ^ Kreyszig, pp. 124-128
- ^ Callen, pp. 47-48
- ^ van der Waals, Rowlinson (ed.), pp. 23-27
- ^ van der Waals, pp. 253-258
- ^ DeBoer, 7-16
- ^ van der Waals, Rowlinson (ed.), pp. 23-27, 64-66
- ^ van der Waals, Rowlinson (ed.), p. 66
- ^ Hirschfelder, et al., pp. 252-253
- ^ Hirschfelder, et al., pp. 168-169
- ^ Hewitt, Nigel. "Who was Van der Waals anyway and what has he to do with my Nitrox fill?". Maths for Divers. Archived from the original on 11 March 2020. Retrieved 1 February 2019.
- ^ Valderrama, pp. 1308-1312
- ^ Kontogeorgis, et al., pp. 4626-4633
- ^ Niemeyer, Kyle. "Mixture properties". Computational Thermodynamics. Archived from the original on 2 April 2024. Retrieved 2 April 2024.
- ^ van der Waals, Rowlinson (ed.), p. 69
- ^ Leland, T. W., Rowlinson, J.S., Sather, G.A., and Watson, I.D., Trans. Faraday Soc., 65, 1447, (1968)
- ^ van der Waals, Rowlinson (ed.), p. 69-70
- ^ van der Waals, Rowlinson (ed.), p. 70
- ^ Goodstein, p. 443
- ^ Korteweg, p. 277
- ^ Tonks, pp. 962-963
- ^ Kac, et al. p. 224.
- ^ Goodstein, p. 446
- ^ Goodstein, pp. 51, 61-68
- ^ Tien and Lienhard, pp. 241-252
- ^ Hirschfelder, et al., pp. 132-141
- ^ Hill, pp. 112-119
- ^ Hirschfelder, et al., p. 133
- ^ Kac, et al., p. 223.
- ^ Korteweg, p. 277.
- ^ van der Waals, (1910), p.256
- ^ van Hove, p.951
- ^ Korteweg, p. 153.
- ^ Rayleigh, p.81 footnote 1
- ^ Tonks, p. 959
- ^ Kac, p. 224
- ^ Kac
- ^ Kac, et al., p216-217
- ^ Kac, et al., p. 224
- ^ Lebowitz and Penrose, p.98
- ^ Lebowitz, pp. 50-52
- ^ Hill, pp. 24,262
- ^ Hill, pp. 262-265
- ^ Hinch, pp. 21-21
- ^ Cole, pp. 1-2
- ^ Goodstein, p. 263
- ^ Tien, and Lienhard, p. 250
- ^ Hill, p. 208
- ^ Hirschfelder, et al., pp. 156-173
- ^ Hill, pp. 270-271
- ^ Tien, and Lienhard, p.251
- ^ Korteweg, p.
- ^ Rowlinson, p. 20
- ^ Alder, et al., P. 143
- ^ Singer, J.V.R., and Singer, K., Mol. Phys.(1972), 24, 357; McDonald, J.R., (1972), 24, 391
- ^ Alder, et al., p. 144
- ^ Valderrama, p. 1606
- ^ Vera and Prausnitz, p. 7-10
- ^ Kontogeorgis, et al., pp. 4626-4629
- ^ Boltzmann, p. 356
References
[edit]- Alder, B. J.; Alley, W. E.; Rigby, M. (1974). "Correction to the van der Waals model for mixtures and for the diffusion coefficient". Physica. 74 (1): 143–155. Bibcode:1974Phy....73..143A. doi:10.1016/0031-8914(74)90231-6.
- Barenblatt, G.I. (1979) [1978 in Russian]. Similarity, Self-Similarity, and Intermediate Asymptotics. Translated by Stein, Norman. Translation Editor VanDyke, Milton. NY and London. Consultants Bureau.
- Barrufet, M.A.; Eubank, P.T. (1989). "Generalized Saturation Properties of Pure Fluids Via Cubic Equations of State". Chemical Engineering Education. 23 (3): 168–175.
- Boltzmann, L. (1995) [1896 (Part I), 1898 (Part II) in German]. Lectures on Gas Theory. Translated by Brush, S.G. NY: Dover.
- Callen, H.B. (1960). Thermodynamics. NY: John Wiley ans Sons.
- DeBoer, J. (1974). "Van der Waals in his time and the present revival opening address". Physica. 73 (1): 1–27. Bibcode:1974Phy....73....1D. doi:10.1016/0031-8914(74)90223-7.
- Dong, W.G.; Lienhard, J.H. (1986). "Corresponding States Correlation of Saturated and Metastable Properties". Canad J Chem Eng. 64: 158–161. doi:10.1002/cjce.5450640123.
- Epstein, P.S. (1937). Textbook of Thermodynamics. NY: John Wiley and Sons.
- Gibbs, J.W. (1948) [1901]. The Collected Works of J. Willard Gibbs Volume II Part One Elementary Principles in Statistical Mechanics. New Haven: Yale University Press.
- Goodstein, D.L. (1985) [1975]. States of Matter. NY: Dover.
- Hill, Terrell L. (1986). Statistical Thermodynamics. NY: Dover.
- Hirschfelder, J. O.; Curtis, C. F.; Bird, R. B. (1964). Mollecular Theory of Gases and Liquids, corrected printing. NY: John Wiley and Sons, Inc.
- Johnston, D.C. (2014). Advances in Thermodynamics of the van der Waals Fluid. arXiv:1402.1205. Bibcode:2014atvd.book.....J. doi:10.1088/978-1-627-05532-1. ISBN 978-1-627-05532-1.
- Kac, Marc (1958). "On the Partition Function of a One-Dimensional Gas". Phys Fluids. 1: 8–12.
- Kac, M.; Uhlenbeck, G.E.; Hemmer, P.C. (1963). "On the van der Waals Theory of the Vapor-Liquid Equilibrium. 1. Discussion of a One-Dimensional Model". J. Math. Phys. 4 (2): 216–228. Bibcode:1963JMP.....4..216K. doi:10.1063/1.1703946.
- Kreyszig, E. (1959). Differential Geometry. Toronto: University of Toronto Press.
- Klein, M. J. (1974). "The Historical Origins of the Van der Waals Equation". Physica. 73 (1): 28–47. Bibcode:1974Phy....73...28K. doi:10.1016/0031-8914(74)90224-9.
- Kontogeorgis, G.M.; Privat, R.; Jaubert, J-N.J. (2019). "Taking Another Look at the van der Waals Equation of State---Amost 150 Years Later". J. Chem. Eng. Data. 64 (11): 4619–4637. doi:10.1021/acs.jced.9b00264.
- Korteweg, D.T. (1891). "On Van Der Waals Isothermal Equation". Nature. 45 (1155): 152–154. Bibcode:1891Natur..45..152K. doi:10.1038/045152a0.
- Korteweg, D.T. (1891). "On Van Der Waals Isothermal Equation". Nature. 45 (1160): 277. doi:10.1038/045277a0.
- Lebowitz, J.L. (1974). "Exact Derivation of the Van Der Waals Equation". Physica. 73 (1): 48–60. Bibcode:1974Phy....73...48L. doi:10.1016/0031-8914(74)90225-0.
- Lebowitz, J.L.; Penrose, O. (1966). "Rigorous Treatment of the Van der Waals-Maxwell Theory of the Liquid-Vapor Transition". Jour Math Phys. 7 (1): 98–113. Bibcode:1966JMP.....7...98L. doi:10.1063/1.1704821.
- Lekner, J. (1982). "Parametric solution of the van der Waals liquid–vapor coexistence curve". Am. J. Phys. 50 (2): 161–163. Bibcode:1982AmJPh..50..161L. doi:10.1119/1.12877.
- Lienhard, J.H. (1986). "The Properties and Behavior of Superheated Liquids". Lat. Am. J. Heat and Mass Transfer. 10: 169–187.
- Lienhard, J.H; Shamsundar, N.; Biney, P.O. (1986). "Spinodal Lines and Equations of State: A Review". Nuclear Engineering and Design. 95: 297–314. Bibcode:1986NuEnD..95..297L. doi:10.1016/0029-5493(86)90056-7.
- Maxwell, J.C. (1875). "On the Dynamical Evidence of the Molecular Constitution of Bodies". Nature. 11 (279): 357–359. Bibcode:1875Natur..11..357C. doi:10.1038/011357a0.
- Moran, M.J.; Shapiro, H.N. (2000). Fundamentals of Engineering Thermodynamics 4th Edition. NY: McGraw-Hill.
- Peck, R.E. (1982). "The Assimilation of van der Waals Equation in the Corresponding States Family". Can. J. Chem. Eng. 60: 446–449. doi:10.1002/cjce.5450600319.
- Pitzer, K.S.; Lippman, D.Z.; Curl, R.F.; Huggins, C.M.; Peterson, D.E. (1955). "The Volumetric and Thermodynamic Properties of Fluids. II. Compressibility Factor, Vapor Pressure and Entropy of Vaporization". J. Am. Chem. Soc. 77 (13): 3433–3440. Bibcode:1955JAChS..77.3433P. doi:10.1021/ja01618a002.
- Shamsundar, N.; Lienhard, J.H. (1983). "Saturation and Metastable Properties of the van der Waals Fluid". Canad J Chem Eng. 61 (6): 876–880. doi:10.1002/cjce.5450610617.
- Sommerfeld, A. (1956). Bopp, F.; Meixner, J. (eds.). Thermodynamics and Statistical Mechanics - Lectures on Theoretical Physics Volume V. Translated by Kestin, J. NY: Academic Press.
- Strutt, J.W., 3rd Baron Rayleigh (1891). "On the Virial of a System of Hard Colliding Bodies". Nature. 45 (1152): 80–82. Bibcode:1891Natur..45...80R. doi:10.1038/045080a0.
{{cite journal}}: CS1 maint: multiple names: authors list (link) CS1 maint: numeric names: authors list (link)
- Tien, C.L.; Lienhard, J.H. (1979). Statistical Thermodynamics Revised Printing. NY: Hemisphere Publishing. Bibcode:1979wdch.book.....T.
- Tonks, L. (1936). "The Complete Equation of State of One, Two, and Three-Dimensional Gases of Hard Elastic Spheres". Phys. Rev. 50 (10): 955–963. Bibcode:1936PhRv...50..955T. doi:10.1103/PhysRev.50.955.
- Truesdell, C.; Bharatha, S. (1977). Classical Thermodynamics as a Theory of Heat Engines. NY: Springer-Verlag.
- Valderrama, J.O. (2003). "The State of the Cubic Equations of State". Ind. Chem. Eng. Res. 42 (8): 1603–1618. doi:10.1021/ie020447b.
- van der Waals, J.D. (1984). Rowlinson, J.S. (ed.). On the Continuity of the Gaseous and Liquid States, edited and with an Introduction by J.S. Rowlinson. NY: Dover Phoenix Editions.
- van der Waals, Johannes D. (1967). "The Equation of State of Gases and Liquids". in Nobel Lectures, Physics 1901-1921. Amsterdam: Elsevier. pp. 254–265.
- van Hove, L. (1949). "Quelques Proprieties Generales De L'Integrale De Configuration D'Un Systeme De Particules Avec Interaction". Physica. 15 (11–12): 951–961. Bibcode:1949Phy....15..951V. doi:10.1016/0031-8914(49)90059-2.
- Van Wylen, G.J.; Sonntag, R.E. (1973). Fundamentals of Classical Thermodynamics Second Edition. NY: John Wiley ans Sons.
- Vera, J.H.; Prausnitz, J.M. (1972). "Generalized van der Waals Theory for Dense Fluids". Chem. Eng. Jour. 3: 1–13. doi:10.1016/0300-9467(72)85001-9.
- Weinberg, S. (2021). Foundations of Modern Physics. Cambridge: Cambridge University Press.
- Whitman, A.M. (2023). Thermodynamics: Basic Principles and Engineering Applications 2nd Edition. NY: Springer.
See also
[edit]- Gas laws
- Ideal gas
- Inversion temperature
- Iteration
- Maxwell construction
- Real gas
- Theorem of corresponding states
- Van der Waals constants (data page)
- Redlich–Kwong equation of state
Further reading
[edit]- Chandler, David (1987). Introduction to Modern Statistical Mechanics. Oxford: Oxford University Press. pp. 287–295. ISBN 0195042778.
- Cross, Michael (2004), "Lecture 3: First Order Phase Transitions" (PDF), Physics 127: Statistical Physics, Second Term, Pasadena, California: Division of Physics, Mathematics, and Astronomy, California Institute of Technology.
- Dalgarno, A.; Davison, W.D. (1966). "The Calculation of Van Der Waals Interactions". Advances in Atomic and Molecular Physics. 2: 1–32. Bibcode:1966AdAMP...2....1D. doi:10.1016/S0065-2199(08)60216-X. ISBN 9780120038022.
- Kittel, Charles; Kroemer, Herbert (1980). Thermal Physics (Revised ed.). New York: Macmillan. pp. 287–295. ISBN 0716710889.























![{\displaystyle b=4N_{\text{A}}[(4\pi /3)(\sigma /2)^{3}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/40a1f623c01cd35e25027f93426a150b48888760)



































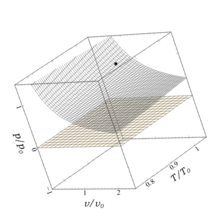
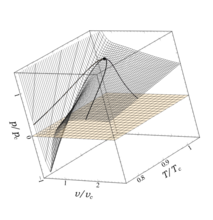






















































![{\displaystyle u-C_{u}=\int \,c_{v}(v,T)\,dT+\int \,\left[T{\frac {\partial p}{\partial T}}-p(v,T)\right]\,dv=\int \,c_{v}(v,T)\,dT+\int \,\left[T^{2}{\frac {\partial (p/T)}{\partial T}}\right]\,dv}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5b5c6fdc48d2c202b9965ec4fd5f10b5b7f05b8)





![{\displaystyle \partial _{v}c(v,T)=\partial _{T}[T^{2}\partial _{T}(p/T)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/046daf6f6bd831ccc4e3c3d412e51dfddac4bc84)
















![{\displaystyle S-C_{s}=R\ln[T^{c}(v-b)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00cf6d99a3f8dfdeb156109e264761edc7c10cf1)
![{\displaystyle S_{r}-{\mbox{C}}_{s}=\ln[T_{r}^{c}(3v_{r}-1)].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f535413e252949d9642506341f817d1ae4a70fd3)

![{\displaystyle f=C_{u}+cT-{a \over v}-T\left(C_{s}+R\ln[T^{c}(v-b)]\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/363780811621b972606b51c4ee682974d1dab087)
![{\displaystyle f_{r}={\mbox{C}}_{u}+cT_{r}-{9 \over 8v_{r}}-T_{r}\left({\mbox{C}}_{s}+\ln[T_{r}^{c}(3v_{r}-1)]\right).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1265d578116c647540670b2ba1af4adcb8547f51)

![{\displaystyle g-C_{u}=\left(c+{v \over v-b}-C_{s}-\ln[T^{c}(v-b)]\right)RT-{2a \over v}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de92dfcb19076bd16b6af57b9a0d5c26a21b621d)
![{\displaystyle g_{r}-{\mbox{C}}_{u}=\left(c+{3v_{r} \over 3v_{r}-1}-{\mbox{C}}_{s}-\ln[T_{r}^{c}(3v_{r}-1)]\right)T_{r}-{9 \over 4v_{r}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8412021e43287ce4b324800d3f1a1085ba4146ef)


















































![{\displaystyle RT_{s}\left[{\frac {v_{g}}{v_{g}-b}}-{\frac {v_{f}}{v_{f}-b}}-\ln \left({\frac {v_{g}-b}{v_{f}-b}}\right)\right]-2a\left({\frac {1}{v_{g}}}-{\frac {1}{v_{f}}}\right)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ab6a6c73e1a07ed0b18db7842da415f6e272aaf)
![{\displaystyle T_{rs}(y)=\left({\frac {27}{8}}\right){\frac {2f(y)[\cosh y+f(y)]}{g(y)^{2}}}\quad p_{rs}=27{\frac {f(y)^{2}[1-f(y)^{2}]}{g(y)^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36ad05293c2155c435125ace832fe508def8706)

















![{\displaystyle \omega =-{\mbox{log}}_{10}[p_{r}(T_{r}=0.7)]-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a2013a671e6051cc544e508d136a89294b175c8)













































































































































![{\displaystyle {\begin{aligned}f_{r}&=u_{r}-T_{r}S_{r}\\&={\mbox{C}}_{u}+T_{r}\left(c-{\mbox{C}}_{s}-\ln[T_{r}^{c}(3v_{r}-1)]\right)-{9 \over {8v_{r}}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ff7305549affc3de3dc072c539630cca806944fc)





























![{\displaystyle \sigma _{x}^{3}=\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\qquad {\mbox{and}}\qquad \epsilon _{x}=\left[\sum _{i=1}^{n}\sum _{j=1}^{n}\epsilon _{ij}\sigma _{ij}^{3}x_{i}x_{j}\right]\left[\sum _{i=i}^{n}\sum _{j=1}^{n}\,\sigma _{ij}^{3}x_{i}x_{j}\right]^{-1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9a745a9d87b00bab563bbea540cfacf610a22d5f)


![{\displaystyle Q_{N}=\Lambda ^{-3N}N!^{-1}{\cal {Z}}_{N}\qquad {\mbox{with}}\qquad {\cal {Z}}_{N}=\int _{V^{\bf {N}}}\,\exp[-\Phi ({\bf {r^{N}}})/kT]\,d{\bf {r^{N}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fac435e93d98e032242bcc43af54b37927ea0b94)

















![{\displaystyle N_{\text{A}}F/N=f=-RT[\ln(n_{Q}v/N_{\text{A}})+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4ffcdfd80234eaee7bdfcee211f830961efdd7f)














































































![{\displaystyle f({\bf {r}}_{12})=\exp[-(\varepsilon /kT){\bar {\varphi }}({\bf {r}}_{12})]-1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97bcc3304e8393c56c23eea97e19f657bf1fa0ef)







![{\displaystyle \exp[-\varphi (r)/(kT)]\approx 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c5e6f5c4663328cc3da5a07b627df55ef483ec3d)
















![{\displaystyle {\begin{aligned}Z&=1+[b_{N}-{{a_{N}} \over {kT}}+O(\tau ^{2})]\rho _{N}+O(\rho _{N}^{2}b_{N}^{2})\\&\sim 1+\left(1-{{a} \over {bRT}}\right)\rho b+O(\rho ^{2}b^{2})+O(\tau ^{2}\rho b)\\&=1+\rho b-{{\rho a} \over {RT}}+O(\rho ^{2}b^{2})+O(\tau ^{2}\rho b).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfd76ba10043e7b4a2366b62e8e23342cb38b1b3)








