Formulations of special relativity
This article needs additional citations for verification. (July 2023) |
| Special relativity |
|---|
 |
The theory of special relativity was initially developed in 1905 by Albert Einstein. However, other interpretations of special relativity have been developed, some on the basis of different foundational axioms. While some are mathematically equivalent to Einstein's theory, others aim to revise or extend it.
Einstein's formulation was based on two postulates, as detailed below. Some formulations modify these postulates or attempt to derive the second postulate by deduction. Others differ in their approach to the geometry of spacetime and the linear transformations between frames of reference.
Einstein's two postulates
[edit]As formulated by Albert Einstein in 1905, the theory of special relativity was based on two main postulates:
- The principle of relativity: The form of a physical law is the same in any inertial frame (a frame of reference that is not accelerating in any direction).
- The speed of light is constant: In all inertial frames, the speed of light c is the same whether the light is emitted from a source at rest or in motion. (Note that this does not apply in non-inertial frames, indeed between accelerating frames the speed of light cannot be constant.[1] Although it can be applied in non-inertial frames if an observer is confined to making local measurements.[2])
Einstein developed the theory of special relativity based on these two postulates. This theory made many predictions which have been experimentally verified, including the relativity of simultaneity, length contraction, time dilation, the relativistic velocity addition formula, the relativistic Doppler effect, relativistic mass, a universal speed limit, mass–energy equivalence, the speed of causality and the Thomas precession.[3][4]
Single-postulate approaches
[edit]Several physicists have derived a theory of special relativity from only the first postulate – the principle of relativity – without assuming the second postulate that the speed of light is constant.[1][5][6][7] The term "single-postulate" is misleading because these formulations may rely on unsaid assumptions such as the cosmological principle, that is, the isotropy and homogeneity of space.[8][9] As such, the term does not refer to the exact number of postulates, but is rather used to distinguish such approaches from the "two-postulate" formulation. Single postulate approaches generally deduce, rather than assume, that the speed of light is constant.
Without assuming the second postulate, the Lorentz transformations can be obtained. However, there is a free parameter k, which renders it incapable of making experimental predictions unless further assumptions are made. The case k = 0 is equivalent to Newtonian physics.[10]
Lorentz ether theory
[edit]Hendrik Lorentz and Henri Poincaré developed their version of special relativity in a series of papers from about 1900 to 1905. They used Maxwell's equations and the principle of relativity to deduce a theory that is mathematically equivalent to the theory later developed by Einstein.
Taiji relativity
[edit]Taiji relativity is a formulation of special relativity developed by Jong-Ping Hsu and Leonardo Hsu.[1][11][12][13] The name of the theory, Taiji, is a Chinese word which refers to ultimate principles which predate the existence of the world. Hsu and Hsu claimed that measuring time in units of distance allowed them to develop a theory of relativity without using the second postulate in their derivation.
It is the principle of relativity, that Hsu & Hsu say, when applied to 4D spacetime, implies the invariance of the 4D-spacetime interval . The difference between this and the spacetime interval in Minkowski space is that is invariant purely by the principle of relativity whereas requires both postulates. The "principle of relativity" in spacetime is taken to mean invariance of laws under 4-dimensional transformations. They claim that there are versions of relativity which are consistent with experiment but have a definition of time where the "speed" of light is not constant. They develop one such version called common relativity which is more convenient for performing calculations for "relativistic many body problems" than using special relativity.
Several authors have made the case that Taiji relativity still assumes a further postulate – the cosmological principle that time and space look the same in all directions.[14] Behara (2003) wrote that "the postulation on the speed of light in special relativity is an inevitable consequence of the relativity principle taken in conjunction with the idea of the homogeneity and isotropy of space and the homogeneity of time in all inertial frames".[15]
Test theories of special relativity
[edit]Test theories of special relativity are flat spacetime theories which are used to test the predictions of special relativity. They differ from the two-postulate special relativity by differentiating between the one-way speed of light and the two-way speed of light. This results in different notions of time simultaneity. There is Robertson's test theory (1949) which predicts different experimental results from Einstein's special relativity, and there is the Mansouri–Sexl theory (1977) which is equivalent to Robertson's theory. There is also Edward's theory (1963) which cannot be called a test theory because it is physically equivalent to special relativity.[16]
Geometric formulations
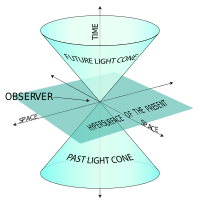
[edit]Minkowski spacetime
[edit]Minkowski space (or Minkowski spacetime) is a mathematical setting in which special relativity is conveniently formulated. Minkowski space is named for the German mathematician Hermann Minkowski, who around 1907 realized that the theory of special relativity (previously developed by Poincaré and Einstein) could be elegantly described using a four-dimensional spacetime, which combines the dimension of time with the three dimensions of space.
Mathematically, there are a number of ways in which the four-dimensions of Minkowski spacetime are commonly represented: as a four-vector with 4 real coordinates, as a four-vector with 3 real and one complex coordinate, or using tensors.
Spacetime algebra
[edit]Spacetime algebra is a type of geometric algebra that is closely related to Minkowski space, and is equivalent to other formalisms of special relativity. It uses mathematical objects such as bivectors to replace tensors in traditional formalisms of Minkowski spacetime, leading to much simpler equations than in matrix mechanics or vector calculus.
de Sitter relativity
[edit]According to the works of Cacciatori, Gorini, Kamenshchik,[7] Bacry and Lévy-Leblond[17] and the references therein, if you take Minkowski's ideas to their logical conclusion, then not only are boosts non-commutative but translations are also non-commutative. This means that the symmetry group of space time is a de Sitter group rather than the Poincaré group. This results in spacetime being slightly curved even in the absence of matter or energy. This residual curvature is caused by a cosmological constant to be determined by observation. Due to the small magnitude of the constant, the special relativity with the Poincaré group is more than accurate enough for all practical purposes, although near the Big Bang and inflation de Sitter relativity may be more useful due to the cosmological constant being larger back then. Note this is not the same thing as solving Einstein's field equations for general relativity to get a de Sitter Universe, rather the de Sitter relativity is about getting a de Sitter Group for special relativity which neglects gravity.
Euclidean relativity
[edit]Euclidean relativity[18][19][20][21][22][23][24] uses a Euclidean (++++) metric in four-dimensional Euclidean space as opposed to the traditional Minkowski (+---) or (-+++) metric in four-dimensional space-time.[a] The Euclidean metric is derived from the Minkowski metric by rewriting into the equivalent . The roles of time t and proper time have switched so that proper time takes the role of the coordinate for the 4th spatial dimension. A universal velocity for all objects moving through four-dimensional space appears from the regular time derivative . The approach differs from the so-called Wick rotation or complex Euclidean relativity. In Wick rotation, time is replaced by , which also leads to a positive definite metric, but it maintains proper time as the Lorentz invariant value whereas in Euclidean relativity becomes a coordinate. Because implies that photons travel at the speed of light in the subspace {x, y, z} and baryonic matter that is at rest in {x, y, z} travels normal to photons along , a paradox arises on how photons can be propagated in a space-time. The possible existence of parallel space-times or parallel worlds shifted and co-moving along is the approach of Giorgio Fontana.[25] Euclidean geometry is consistent with Minkowski's classical theory of relativity. When the geometric projection of 4D properties to 3D space is made, the hyperbolic Minkowski geometry transforms into a rotation in 4D circular geometry.
Very special relativity
[edit]Ignoring gravity, experimental bounds seem to suggest that special relativity with its Lorentz symmetry and Poincaré symmetry describes spacetime. Cohen and Glashow[26] have demonstrated that a small subgroup of the Lorentz group is sufficient to explain all the current bounds.
The minimal subgroup in question can be described as follows: The stabilizer of a null vector is the special Euclidean group SE(2), which contains T(2) as the subgroup of parabolic transformations. This T(2), when extended to include either parity or time reversal (i.e. subgroups of the orthochronous and time-reversal respectively), is sufficient to give us all the standard predictions. Their new symmetry is called Very Special Relativity (VSR).
Doubly special relativity
[edit]Doubly special relativity (DSR) is a modified theory of special relativity in which there is not only an observer-independent maximum velocity (the speed of light), but an observer-independent minimum length (the Planck length).
The motivation to these proposals is mainly theoretical, based on the following observation: the Planck length is expected to play a fundamental role in a theory of quantum gravity, setting the scale at which quantum gravity effects cannot be neglected and new phenomena are observed. If special relativity is to hold up exactly to this scale, different observers would observe quantum gravity effects at different scales, due to the Lorentz–FitzGerald contraction, in contradiction to the principle that all inertial observers should be able to describe phenomena by the same physical laws.
A drawback of the usual doubly special relativity models is that they are valid only at the energy scales where ordinary special relativity is supposed to break down, giving rise to a patchwork relativity. On the other hand, de Sitter relativity is found to be invariant under a simultaneous re-scaling of mass, energy and momentum, and is consequently valid at all energy scales.
See also
[edit]- Alternative derivations of special relativity
- Derivations of the Lorentz transformations
- History of special relativity
Notes
[edit]- ^ The Minkowski metric describes four-dimensional space-time: the coordinates are time and three spatial dimensions. The Euclidean metric describes four-dimensional Euclidean space: it has four spatial coordinates.
References
[edit]- ^ a b c Hsu, J.-P.; Hsu, L. (2006). A Broader View of Relativity. World Scientific. ISBN 981-256-651-1.
- ^ Petkov, Vesselin (2006). Relativity and the Nature of Spacetime (illustrated ed.). Springer Science & Business Media. p. 193. ISBN 978-3-540-27700-2. Extract of page 193
- ^ Griffiths, David J. (2013). "Electrodynamics and Relativity". Introduction to Electrodynamics (4th ed.). Pearson. Chapter 12. ISBN 978-0-321-85656-2.
- ^ Jackson, John D. (1999). "Special Theory of Relativity". Classical Electrodynamics (3rd ed.). John Wiley & Sons, Inc. Chapter 11. ISBN 0-471-30932-X.
- ^ von Ignatowsky, W. (1911). "Das Relativitätsprinzip". Archiv der Mathematik und Physik (in German). 17: 1.
- ^ Feigenbaum, M. J. (2008). "The Theory of Relativity – Galileo's Child". arXiv:0806.1234 [physics.class-ph].
- ^ a b Cacciatori, S.; Gorini, V.; Kamenshchik, A. (2008). "Special relativity in the 21st century". Annalen der Physik. 520 (9–10): 728–768. arXiv:0807.3009. Bibcode:2008AnP...520..728C. doi:10.1002/andp.200810321. S2CID 119191753.
- ^ C., E. (November 1924). "The Mathematical Theory of Relativity". Nature. 114 (2874): 782–783. Bibcode:1924Natur.114..782C. doi:10.1038/114782a0. ISSN 1476-4687. S2CID 4064705.
- ^ Einstein, A. (1921). Morgan document.[full citation needed]
- ^ Drory, Alon (1 August 2015). "The necessity of the second postulate in special relativity". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics. 51: 57–67. arXiv:1412.4018. Bibcode:2015SHPMP..51...57D. doi:10.1016/j.shpsb.2014.08.015. ISSN 1355-2198.
- ^
Hsu, J.-P.; Hsu, L. (1994). "A physical theory based solely on the first postulate of relativity". Physics Letters A. 196 (1–2): 1–6. Bibcode:1994PhLA..196....1H. doi:10.1016/0375-9601(94)91033-2.
- Erratum Hsu, Jong-Ping; Hsu, Leonardo (1996). "A physical theory based solely on the first postulate of relativity (Physics Letters a 196 (1994)1)". Physics Letters A. 217 (6): 359. Bibcode:1996PhLA..217..359H. doi:10.1016/0375-9601(96)00329-5.
- ^ Hsu, J.-P.; Hsu, L. (2008). "Experimental tests of a new Lorentz-invariant dynamics based solely on the first postulate of relativity". Il Nuovo Cimento B. 111 (11): 1283–1297. Bibcode:1996NCimB.111.1283H. doi:10.1007/BF02742506. S2CID 120483040.
- ^ Hsu, J.-P.; Hsu, L. (2008). "Four-dimensional symmetry of taiji relativity and coordinate transformations based on a weaker postulate for the speed of light". Il Nuovo Cimento B. 111 (11): 1299–1313. Bibcode:1996NCimB.111.1299H. doi:10.1007/BF02742507. S2CID 119831503.
- ^ Ai, Xiao-Bai (1996). "On the Basis of Taiji Relativity". Chinese Physics Letters. 13 (5): 321–324. Bibcode:1996ChPhL..13..321A. doi:10.1088/0256-307X/13/5/001. S2CID 250777204.
- ^ Behera, H. (2003). "A comment on the Invariance of the Speed of Light". Bulletin of Orissa Physical Society. 10: 4087. arXiv:physics/0304087. Bibcode:2003physics...4087B.
- ^ Zhang, Y.-Z. (1997). Special Relativity and Its Experimental Foundations. World Scientific. ISBN 978-981-02-2749-4.
- ^ Bacry, H.; Lévy-Leblond, J.-M. (1968). "Possible Kinematics". Journal of Mathematical Physics. 9 (10): 1605–1614. Bibcode:1968JMP.....9.1605B. doi:10.1063/1.1664490.
- ^ Yamashita, Takuya (May 2023). "Theoretical Evidence for Principles of Special Relativity Based on Isotropic and Uniform Four-Dimensional Space". Preprints. doi:10.20944/preprints202305.1785.v1.
- ^ Hans, H. (2001). "Proper time formulation of relativistic dynamics". Foundations of Physics. 31 (9): 1357–1400. Bibcode:2001FoPh...31.1357M. doi:10.1023/A:1012274211780. S2CID 117357649.
- ^ Gersten, A. (2003). "Euclidean special relativity". Foundations of Physics. 33 (8): 1237–1251. Bibcode:2003FoPh...33.1237G. doi:10.1023/A:1025631125442. S2CID 15496801.
- ^ van Linden, R. F. J. (2006). "Minkowski versus Euclidean 4-vectors" (PDF).
- ^ Crabbe, A. (2004). "Alternative conventions and geometry for Special Relativity" (PDF). Annales de la Fondation Louis de Broglie. 29 (4): 589–608.
- ^ Almeida, J. (2001). "An alternative to Minkowski space-time". arXiv:gr-qc/0104029.
- ^ "Euclidean relativity portal". 28 September 2012. Retrieved 23 July 2014.
- ^ Fontana, G. (2005). "The Four Space-times Model of Reality". AIP Conference Proceedings. 746: 1403–1410. arXiv:physics/0410054. Bibcode:2005AIPC..746.1403F. doi:10.1063/1.1867271. S2CID 118189976.
- ^ Cohen, Andrew G.; Glashow, Sheldon L. (2006). "Very special relativity". Physical Review Letters. 97 (2): 1601. arXiv:hep-ph/0601236. Bibcode:2006PhRvL..97b1601C. doi:10.1103/PhysRevLett.97.021601. PMID 16907430. S2CID 11056484.










