Random sample consensus
| Part of a series on |
| Machine learning and data mining |
|---|
Random sample consensus (RANSAC) is an iterative method to estimate parameters of a mathematical model from a set of observed data that contains outliers, when outliers are to be accorded no influence[clarify] on the values of the estimates. Therefore, it also can be interpreted as an outlier detection method.[1] It is a non-deterministic algorithm in the sense that it produces a reasonable result only with a certain probability, with this probability increasing as more iterations are allowed. The algorithm was first published by Fischler and Bolles at SRI International in 1981. They used RANSAC to solve the location determination problem (LDP), where the goal is to determine the points in the space that project onto an image into a set of landmarks with known locations.
RANSAC uses repeated random sub-sampling.[2] A basic assumption is that the data consists of "inliers", i.e., data whose distribution can be explained by some set of model parameters, though may be subject to noise, and "outliers", which are data that do not fit the model. The outliers can come, for example, from extreme values of the noise or from erroneous measurements or incorrect hypotheses about the interpretation of data. RANSAC also assumes that, given a (usually small) set of inliers, there exists a procedure that can estimate the parameters of a model optimally explaining or fitting this data.
Example
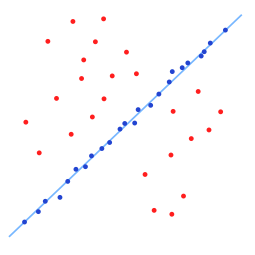
[edit]A simple example is fitting a line in two dimensions to a set of observations. Assuming that this set contains both inliers, i.e., points which approximately can be fitted to a line, and outliers, points which cannot be fitted to this line, a simple least squares method for line fitting will generally produce a line with a bad fit to the data including inliers and outliers. The reason is that it is optimally fitted to all points, including the outliers. RANSAC, on the other hand, attempts to exclude the outliers and find a linear model that only uses the inliers in its calculation. This is done by fitting linear models to several random samplings of the data and returning the model that has the best fit to a subset of the data. Since the inliers tend to be more linearly related than a random mixture of inliers and outliers, a random subset that consists entirely of inliers will have the best model fit. In practice, there is no guarantee that a subset of inliers will be randomly sampled, and the probability of the algorithm succeeding depends on the proportion of inliers in the data as well as the choice of several algorithm parameters.
-
A data set with many outliers for which a line has to be fitted.
-
Fitted line with RANSAC; outliers have no influence on the result.
Overview
[edit]The RANSAC algorithm is a learning technique to estimate parameters of a model by random sampling of observed data. Given a dataset whose data elements contain both inliers and outliers, RANSAC uses the voting scheme to find the optimal fitting result. Data elements in the dataset are used to vote for one or multiple models. The implementation of this voting scheme is based on two assumptions: that the noisy features will not vote consistently for any single model (few outliers) and there are enough features to agree on a good model (few missing data). The RANSAC algorithm is essentially composed of two steps that are iteratively repeated:
- A sample subset containing minimal number of data items is randomly selected from the input dataset. A fitting model with model parameters is computed using only the elements of this sample subset. The cardinality of the sample subset (e.g., the amount of data in this subset) is sufficient to determine the model parameters.
- The algorithm checks which elements of the entire dataset are consistent with the model instantiated by the estimated model parameters obtained from the first step. A data element will be considered as an outlier if it does not fit the model within some error threshold defining the maximum data deviation of inliers (data elements beyond this deviation are outliers).
The set of inliers obtained for the fitting model is called the consensus set. The RANSAC algorithm will iteratively repeat the above two steps until the obtained consensus set in certain iteration has enough inliers.
The input to the RANSAC algorithm is a set of observed data values, a model to fit to the observations, and some confidence parameters defining outliers. In more details than the aforementioned RANSAC algorithm overview, RANSAC achieves its goal by repeating the following steps:
- Select a random subset of the original data. Call this subset the hypothetical inliers.
- A model is fitted to the set of hypothetical inliers.
- All data are then tested against the fitted model. All the data points (of the original data) that fit the estimated model well, according to some model-specific loss function, are called the consensus set (i.e., the set of inliers for the model).
- The estimated model is reasonably good if sufficiently many data points have been classified as a part of the consensus set.
- The model may be improved by re-estimating it by using all the members of the consensus set. The fitting quality as a measure of how well the model fits to the consensus set will be used to sharpen the model fitting as iterations goes on (e.g., by setting this measure as the fitting quality criteria at the next iteration).
To converge to a sufficiently good model parameter set, this procedure is repeated a fixed number of times, each time producing either the rejection of a model because too few points are a part of the consensus set, or a refined model with a consensus set size larger than the previous consensus set.

Pseudocode
[edit]The generic RANSAC algorithm works as the following pseudocode:
Given:
data – A set of observations.
model – A model to explain the observed data points.
n – The minimum number of data points required to estimate the model parameters.
k – The maximum number of iterations allowed in the algorithm.
t – A threshold value to determine data points that are fit well by the model (inlier).
d – The number of close data points (inliers) required to assert that the model fits well to the data.
Return:
bestFit – The model parameters which may best fit the data (or null if no good model is found).
iterations = 0
bestFit = null
bestErr = something really large // This parameter is used to sharpen the model parameters to the best data fitting as iterations go on.
while iterations < k do
maybeInliers := n randomly selected values from data
maybeModel := model parameters fitted to maybeInliers
confirmedInliers := empty set
for every point in data do
if point fits maybeModel with an error smaller than t then
add point to confirmedInliers
end if
end for
if the number of elements in confirmedInliers is > d then
// This implies that we may have found a good model.
// Now test how good it is.
betterModel := model parameters fitted to all the points in confirmedInliers
thisErr := a measure of how well betterModel fits these points
if thisErr < bestErr then
bestFit := betterModel
bestErr := thisErr
end if
end if
increment iterations
end while
return bestFit
Example code
[edit]A Python implementation mirroring the pseudocode. This also defines a LinearRegressor based on least squares, applies RANSAC to a 2D regression problem, and visualizes the outcome:
from copy import copy
import numpy as np
from numpy.random import default_rng
rng = default_rng()
class RANSAC:
def __init__(self, n=10, k=100, t=0.05, d=10, model=None, loss=None, metric=None):
self.n = n # `n`: Minimum number of data points to estimate parameters
self.k = k # `k`: Maximum iterations allowed
self.t = t # `t`: Threshold value to determine if points are fit well
self.d = d # `d`: Number of close data points required to assert model fits well
self.model = model # `model`: class implementing `fit` and `predict`
self.loss = loss # `loss`: function of `y_true` and `y_pred` that returns a vector
self.metric = metric # `metric`: function of `y_true` and `y_pred` and returns a float
self.best_fit = None
self.best_error = np.inf
def fit(self, X, y):
for _ in range(self.k):
ids = rng.permutation(X.shape[0])
maybe_inliers = ids[: self.n]
maybe_model = copy(self.model).fit(X[maybe_inliers], y[maybe_inliers])
thresholded = (
self.loss(y[ids][self.n :], maybe_model.predict(X[ids][self.n :]))
< self.t
)
inlier_ids = ids[self.n :][np.flatnonzero(thresholded).flatten()]
if inlier_ids.size > self.d:
inlier_points = np.hstack([maybe_inliers, inlier_ids])
better_model = copy(self.model).fit(X[inlier_points], y[inlier_points])
this_error = self.metric(
y[inlier_points], better_model.predict(X[inlier_points])
)
if this_error < self.best_error:
self.best_error = this_error
self.best_fit = better_model
return self
def predict(self, X):
return self.best_fit.predict(X)
def square_error_loss(y_true, y_pred):
return (y_true - y_pred) ** 2
def mean_square_error(y_true, y_pred):
return np.sum(square_error_loss(y_true, y_pred)) / y_true.shape[0]
class LinearRegressor:
def __init__(self):
self.params = None
def fit(self, X: np.ndarray, y: np.ndarray):
r, _ = X.shape
X = np.hstack([np.ones((r, 1)), X])
self.params = np.linalg.inv(X.T @ X) @ X.T @ y
return self
def predict(self, X: np.ndarray):
r, _ = X.shape
X = np.hstack([np.ones((r, 1)), X])
return X @ self.params
if __name__ == "__main__":
regressor = RANSAC(model=LinearRegressor(), loss=square_error_loss, metric=mean_square_error)
X = np.array([-0.848,-0.800,-0.704,-0.632,-0.488,-0.472,-0.368,-0.336,-0.280,-0.200,-0.00800,-0.0840,0.0240,0.100,0.124,0.148,0.232,0.236,0.324,0.356,0.368,0.440,0.512,0.548,0.660,0.640,0.712,0.752,0.776,0.880,0.920,0.944,-0.108,-0.168,-0.720,-0.784,-0.224,-0.604,-0.740,-0.0440,0.388,-0.0200,0.752,0.416,-0.0800,-0.348,0.988,0.776,0.680,0.880,-0.816,-0.424,-0.932,0.272,-0.556,-0.568,-0.600,-0.716,-0.796,-0.880,-0.972,-0.916,0.816,0.892,0.956,0.980,0.988,0.992,0.00400]).reshape(-1,1)
y = np.array([-0.917,-0.833,-0.801,-0.665,-0.605,-0.545,-0.509,-0.433,-0.397,-0.281,-0.205,-0.169,-0.0531,-0.0651,0.0349,0.0829,0.0589,0.175,0.179,0.191,0.259,0.287,0.359,0.395,0.483,0.539,0.543,0.603,0.667,0.679,0.751,0.803,-0.265,-0.341,0.111,-0.113,0.547,0.791,0.551,0.347,0.975,0.943,-0.249,-0.769,-0.625,-0.861,-0.749,-0.945,-0.493,0.163,-0.469,0.0669,0.891,0.623,-0.609,-0.677,-0.721,-0.745,-0.885,-0.897,-0.969,-0.949,0.707,0.783,0.859,0.979,0.811,0.891,-0.137]).reshape(-1,1)
regressor.fit(X, y)
import matplotlib.pyplot as plt
plt.style.use("seaborn-darkgrid")
fig, ax = plt.subplots(1, 1)
ax.set_box_aspect(1)
plt.scatter(X, y)
line = np.linspace(-1, 1, num=100).reshape(-1, 1)
plt.plot(line, regressor.predict(line), c="peru")
plt.show()
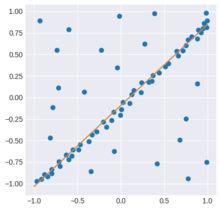
RANSAC implementation. The orange line shows the least-squares parameters found by the iterative approach, which successfully ignores the outlier points.Parameters
[edit]The threshold value to determine when a data point fits a model (t), and the number of inliers (data points fitted to the model within t) required to assert that the model fits well to data (d) are determined based on specific requirements of the application and the dataset, and possibly based on experimental evaluation. The number of iterations (k), however, can be roughly determined as a function of the desired probability of success (p) as shown below.
Let p be the desired probability that the RANSAC algorithm provides at least one useful result after running. In extreme (for simplifying the derivation), RANSAC returns a successful result if in some iteration it selects only inliers from the input data set when it chooses n points from the data set from which the model parameters are estimated. (In other words, all the selected n data points are inliers of the model estimated by these points). Let be the probability of choosing an inlier each time a single data point is selected, that is roughly,
- = number of inliers in data / number of points in data
A common case is that is not well known beforehand because of an unknown number of inliers in data before running the RANSAC algorithm, but some rough value can be given. With a given rough value of and roughly assuming that the n points needed for estimating a model are selected independently (It is a rough assumption because each data point selection reduces the number of data point candidates to choose in the next selection in reality), is the probability that all n points are inliers and is the probability that at least one of the n points is an outlier, a case which implies that a bad model will be estimated from this point set. That probability to the power of k (the number of iterations in running the algorithm) is the probability that the algorithm never selects a set of n points which all are inliers, and this is the same as (the probability that the algorithm does not result in a successful model estimation) in extreme. Consequently,
which, after taking the logarithm of both sides, leads to
This result assumes that the n data points are selected independently, that is, a point which has been selected once is replaced and can be selected again in the same iteration. This is often not a reasonable approach and the derived value for k should be taken as an upper limit in the case that the points are selected without replacement. For example, in the case of finding a line which fits the data set illustrated in the above figure, the RANSAC algorithm typically chooses two points in each iteration and computes maybe_model as the line between the points and it is then critical that the two points are distinct.
To gain additional confidence, the standard deviation or multiples thereof can be added to k. The standard deviation of k is defined as
Advantages and disadvantages
[edit]This section needs additional citations for verification. (September 2014) |
An advantage of RANSAC is its ability to do robust estimation[3] of the model parameters, i.e., it can estimate the parameters with a high degree of accuracy even when a significant number of outliers are present in the data set. A disadvantage of RANSAC is that there is no upper bound on the time it takes to compute these parameters (except exhaustion). When the number of iterations computed is limited, the solution obtained may not be optimal, and it may not even be one that fits the data in a good way. In this way RANSAC offers a trade-off; by computing a greater number of iterations, the probability of a reasonable model being produced is increased. Moreover, RANSAC is not always able to find the optimal set even for moderately contaminated sets, and it usually performs badly when the number of inliers is less than 50%. Optimal RANSAC[4] was proposed to handle both these problems and is capable of finding the optimal set for heavily contaminated sets, even for an inlier ratio under 5%. Another disadvantage of RANSAC is that it requires the setting of problem-specific thresholds.
RANSAC can only estimate one model for a particular data set. As for any one-model approach when two (or more) model instances exist, RANSAC may fail to find either one. The Hough transform is one alternative robust estimation technique that may be useful when more than one model instance is present. Another approach for multi-model fitting is known as PEARL,[5] which combines model sampling from data points as in RANSAC with iterative re-estimation of inliers and the multi-model fitting being formulated as an optimization problem with a global energy function describing the quality of the overall solution.
Applications
[edit]The RANSAC algorithm is often used in computer vision, e.g., to simultaneously solve the correspondence problem and estimate the fundamental matrix related to a pair of stereo cameras; see also: Structure from motion, scale-invariant feature transform, image stitching, rigid motion segmentation.
Development and improvements
[edit]Since 1981 RANSAC has become a fundamental tool in the computer vision and image processing community. In 2006, for the 25th anniversary of the algorithm, a workshop was organized at the International Conference on Computer Vision and Pattern Recognition (CVPR) to summarize the most recent contributions and variations to the original algorithm, mostly meant to improve the speed of the algorithm, the robustness and accuracy of the estimated solution and to decrease the dependency from user defined constants.
RANSAC can be sensitive to the choice of the correct noise threshold that defines which data points fit a model instantiated with a certain set of parameters. If such threshold is too large, then all the hypotheses tend to be ranked equally (good). On the other hand, when the noise threshold is too small, the estimated parameters tend to be unstable ( i.e. by simply adding or removing a datum to the set of inliers, the estimate of the parameters may fluctuate). To partially compensate for this undesirable effect, Torr et al. proposed two modification of RANSAC called MSAC (M-estimator SAmple and Consensus) and MLESAC (Maximum Likelihood Estimation SAmple and Consensus).[6] The main idea is to evaluate the quality of the consensus set ( i.e. the data that fit a model and a certain set of parameters) calculating its likelihood (whereas in the original formulation by Fischler and Bolles the rank was the cardinality of such set). An extension to MLESAC which takes into account the prior probabilities associated to the input dataset is proposed by Tordoff.[7] The resulting algorithm is dubbed Guided-MLESAC. Along similar lines, Chum proposed to guide the sampling procedure if some a priori information regarding the input data is known, i.e. whether a datum is likely to be an inlier or an outlier. The proposed approach is called PROSAC, PROgressive SAmple Consensus.[8]
Chum et al. also proposed a randomized version of RANSAC called R-RANSAC [9] to reduce the computational burden to identify a good consensus set. The basic idea is to initially evaluate the goodness of the currently instantiated model using only a reduced set of points instead of the entire dataset. A sound strategy will tell with high confidence when it is the case to evaluate the fitting of the entire dataset or when the model can be readily discarded. It is reasonable to think that the impact of this approach is more relevant in cases where the percentage of inliers is large. The type of strategy proposed by Chum et al. is called preemption scheme. Nistér proposed a paradigm called Preemptive RANSAC[10] that allows real time robust estimation of the structure of a scene and of the motion of the camera. The core idea of the approach consists in generating a fixed number of hypotheses so that the comparison happens with respect to the quality of the generated hypothesis rather than against some absolute quality metric.
Other researchers tried to cope with difficult situations where the noise scale is not known and/or multiple model instances are present. The first problem has been tackled in the work by Wang and Suter.[11] Toldo et al. represent each datum with the characteristic function of the set of random models that fit the point. Then multiple models are revealed as clusters which group the points supporting the same model. The clustering algorithm, called J-linkage, does not require prior specification of the number of models, nor does it necessitate manual parameters tuning.[12]
RANSAC has also been tailored for recursive state estimation applications, where the input measurements are corrupted by outliers and Kalman filter approaches, which rely on a Gaussian distribution of the measurement error, are doomed to fail. Such an approach is dubbed KALMANSAC.[13]
Related methods
[edit]- MLESAC (Maximum Likelihood Estimate Sample Consensus) – maximizes the likelihood that the data was generated from the sample-fitted model, e.g. a mixture model of inliers and outliers
- MAPSAC (Maximum A Posterior Sample Consensus) – extends MLESAC to incorporate a prior probability of the parameters to be fitted and maximizes the posterior probability
- KALMANSAC – causal inference of the state of a dynamical system
- Resampling (statistics)
- Hop-Diffusion Monte Carlo uses randomized sampling involve global jumps and local diffusion to choose the sample at each step of RANSAC for epipolar geometry estimation between very wide-baseline images.[14]
- FSASAC (RANSAC based on data filtering and simulated annealing)[15]
See also
[edit]Notes
[edit]- ^ Data Fitting and Uncertainty, T. Strutz, Springer Vieweg (2nd edition, 2016).
- ^ Cantzler, H. "Random Sample Consensus (RANSAC)". Institute for Perception, Action and Behaviour, Division of Informatics, University of Edinburgh. CiteSeerX 10.1.1.106.3035. Archived from the original on 2023-02-04.
- ^ Robust Statistics, Peter. J. Huber, Wiley, 1981 (republished in paperback, 2004), page 1.
- ^ Anders Hast, Johan Nysjö, Andrea Marchetti (2013). "Optimal RANSAC – Towards a Repeatable Algorithm for Finding the Optimal Set". Journal of WSCG 21 (1): 21–30.
- ^ Hossam Isack, Yuri Boykov (2012). "Energy-based Geometric Multi-Model Fitting". International Journal of Computer Vision 97 (2: 1): 23–147. doi:10.1007/s11263-011-0474-7.
- ^ P.H.S. Torr and A. Zisserman, MLESAC: A new robust estimator with application to estimating image geometry[dead link], Journal of Computer Vision and Image Understanding 78 (2000), no. 1, 138–156.
- ^ B. J. Tordoff and D. W. Murray, Guided-MLESAC: Faster image transform estimation by using matching priors, IEEE Transactions on Pattern Analysis and Machine Intelligence 27 (2005), no. 10, 1523–1535.
- ^ Matching with PROSAC – progressive sample consensus, Proceedings of Conference on Computer Vision and Pattern Recognition (San Diego), vol. 1, June 2005, pp. 220–226
- ^ O. Chum and J. Matas, Randomized RANSAC with Td,d test, 13th British Machine Vision Conference, September 2002. http://www.bmva.org/bmvc/2002/papers/50/
- ^ D. Nistér, Preemptive RANSAC for live structure and motion estimation, IEEE International Conference on Computer Vision (Nice, France), October 2003, pp. 199–206.
- ^ H. Wang and D. Suter, Robust adaptive-scale parametric model estimation for computer vision., IEEE Transactions on Pattern Analysis and Machine Intelligence 26 (2004), no. 11, 1459–1474
- ^ R. Toldo and A. Fusiello, Robust multiple structures estimation with J-linkage, European Conference on Computer Vision (Marseille, France), October 2008, pp. 537–547.
- ^ A. Vedaldi, H. Jin, P. Favaro, and S. Soatto, KALMANSAC: Robust filtering by consensus, Proceedings of the International Conference on Computer Vision (ICCV), vol. 1, 2005, pp. 633–640
- ^ Brahmachari, Aveek S.; Sarkar, Sudeep (March 2013). "Hop-Diffusion Monte Carlo for Epipolar Geometry Estimation between Very Wide-Baseline Images". IEEE Transactions on Pattern Analysis and Machine Intelligence. 35 (3): 755–762. doi:10.1109/TPAMI.2012.227. PMID 26353140. S2CID 2524656.
- ^ W. Ruoyan and W. Junfeng, "FSASAC: Random Sample Consensus Based on Data Filter and Simulated Annealing," in IEEE Access, vol. 9, pp. 164935-164948, 2021, doi: 10.1109/ACCESS.2021.3135416.
References
[edit]- Martin A. Fischler & Robert C. Bolles (June 1981). "Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography" (PDF). Comm. ACM. 24 (6): 381–395. doi:10.1145/358669.358692. S2CID 972888. Archived (PDF) from the original on December 10, 2014.
- David A. Forsyth & Jean Ponce (2003). Computer Vision, a modern approach. Prentice Hall. ISBN 978-0-13-085198-7.
- Richard Hartley and Andrew Zisserman (2003). Multiple View Geometry in Computer Vision (2nd ed.). Cambridge University Press.
- Strutz, T. (2016). Data Fitting and Uncertainty (A practical introduction to weighted least squares and beyond). 2nd edition, Springer Vieweg. ISBN 978-3-658-11455-8.
- P.H.S. Torr & D.W. Murray (1997). "The Development and Comparison of Robust Methods for Estimating the Fundamental Matrix". International Journal of Computer Vision. 24 (3): 271–300. doi:10.1023/A:1007927408552. S2CID 12031059.
- Ondrej Chum (2005). "Two-View Geometry Estimation by Random Sample and Consensus" (PDF). PhD Thesis.
- Sunglok Choi; Taemin Kim & Wonpil Yu (2009). "Performance Evaluation of RANSAC Family" (PDF). In Proceedings of the British Machine Vision Conference (BMVC). Archived from the original (PDF) on 2020-08-31. Retrieved 2010-10-01.
- Anders Hast; Johan Nysjö; Andrea Marchetti (2013). "Optimal RANSAC – Towards a Repeatable Algorithm for Finding the Optimal Set" (PDF). Journal of WSCG. 21 (1): 21–30.
- Hossam Isack; Yuri Boykov (2012). "Energy-based Geometric Multi-Model Fitting" (PDF). International Journal of Computer Vision. 97 (2: 1): 23–147. CiteSeerX 10.1.1.381.2434. doi:10.1007/s11263-011-0474-7. S2CID 5461268.