Pyramid (geometry)
| Set of pyramids | |
|---|---|
| |
| Faces | n triangles, 1 n-gon |
| Edges | 2n |
| Vertices | n+1 |
| Symmetry group | Cnv |
| Dual polyhedron | Self-duals |
| Properties | convex |
- This article is about the polyhedron pyramid (a 3-dimensional shape); for other versions including architectural Pyramids, see Pyramid (disambiguation).
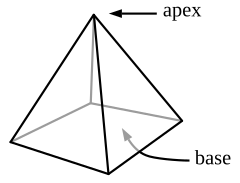
An n-sided pyramid is a polyhedron formed by connecting an n-sided polygonal base and a point, called the apex, by n triangular faces (n ≥ 3). In other words, it is a conic solid with polygonal base.
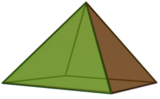
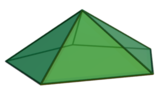
When unspecified, the base is usually assumed to be square. For a triangular pyramid each face can serve as base, with the opposite vertex as apex. The regular tetrahedron, one of the Platonic solids, is a triangular pyramid. The square and pentagonal pyramids can also be constructed with all faces regular, and are therefore Johnson solids. All pyramids are self-dual.
Pyramids are a subclass of the prismatoids. The 1-skeleton of pyramid is a wheel graph.
Volume
The volume of a pyramid is where A is the area of the base and h the height from the base to the apex. This works for any location of the apex, provided that h is measured as the perpendicular distance from the plane which contains the base.
Surface Area
The surface area of a regular pyramid is where is the area of the base, p is the perimeter of the base, and s is the slant height along the bisector of a face (ie the length from the midpoint of any edge of the base to the apex).
Pyramids with regular polygon faces
If all faces are regular polygons, the pyramid base can be a regular polygon of 3, 4 or 5 sided:
| Name | Tetrahedron | Square pyramid | Pentagonal pyramid |
|---|---|---|---|

|
|
| |
| Class | Platonic solid | Johnson solid (J1) | Johnson solid (J2) |
| Base | equilaterial triangle | Square | regular pentagon |
| Symmetry group |
Td | C4v | C5v |
The geometric center of a square-based pyramid is located on the symmetry axis, one quarter of the way from the base to the apex.
Symmetry
If the base is regular and the apex is above the center, the symmetry group of the n-sided pyramid is Cnv of order 2n, except in the case of a regular tetrahedron, which has the larger symmetry group Td of order 24, which has four versions of C3v as subgroups. The rotation group is Cn of order n, except in the case of a regular tetrahedron, which has the larger rotation group T of order 12, which has four versions of C3 as subgroups.
See also
External links
- Weisstein, Eric W. "Pyramid". MathWorld.
- The Uniform Polyhedra
- Spinning Triangular Pyramid, Square Pyramid and Pentagonal Pyramid at Math Is Fun
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRML models (George Hart) <3> <4> <5>
- Paper models of pyramids



