Möbius ladder
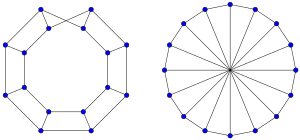
In graph theory, the Möbius ladder Mn is a cubic circulant graph with an even number n of vertices, formed from an n-cycle by adding edges (called "rungs") connecting opposite pairs of vertices in the cycle. It is so-named because (with the exception of M6 = K3,3) Mn has exactly n/2 4-cycles[1] which link together by their shared edges to form a topological Möbius strip. Möbius ladders were named and first studied by Guy and Harary (1967).
Properties
Every Möbius ladder is a nonplanar apex graph, meaning that it cannot be drawn without crossings in the plane but removing one vertex allows the remaining graph to be drawn without crossings. Möbius ladders have crossing number one, and can be embedded without crossings on a torus or projective plane. Thus, they are examples of toroidal graphs. Li (2005) explores embeddings of these graphs onto higher genus surfaces.
Möbius ladders are vertex-transitive – they have symmetries taking any vertex to any other vertex – but (again with the exception of M6) they are not edge-transitive. The edges from the cycle from which the ladder is formed can be distinguished from the rungs of the ladder, because each cycle edge belongs to a single 4-cycle, while each rung belongs to two such cycles. Therefore, there is no symmetry taking a cycle edge to a rung edge or vice versa.
When n ≡ 2 (mod 4), Mn is bipartite. When n ≡ 0 (mod 4), it is not bipartite. The endpoints of each rung are an even distance apart in the initial cycle, so adding each rung creates an odd cycle. In this case, because the graph is 3-regular but not bipartite, by Brooks' theorem it has chromatic number 3. De Mier & Noy (2004) show that the Möbius ladders are uniquely determined by their Tutte polynomials.
The Möbius ladder M8 has 392 spanning trees; it and M6 have the most spanning trees among all cubic graphs with the same number of vertices.[2] However, the 10-vertex cubic graph with the most spanning trees is the Petersen graph, which is not a Möbius ladder.
The Tutte polynomials of the Möbius ladders may be computed by a simple recurrence relation.[3]
Graph minors

Möbius ladders play an important role in the theory of graph minors. The earliest result of this type is a theorem of Klaus Wagner (1937) that graphs with no K5 minor can be formed by using clique-sum operations to combine planar graphs and the Möbius ladder M8; for this reason M8 is called the Wagner graph.
Gubser (1996) defines an almost-planar graph to be a nonplanar graph for which every nontrivial minor is planar; he shows that 3-connected almost-planar graphs are Möbius ladders or members of a small number of other families, and that other almost-planar graphs can be formed from these by a sequence of simple operations.
Maharry (2000) shows that almost all graphs that do not have a cube minor can be derived by a sequence of simple operations from Möbius ladders.
Chemistry and physics
Walba, Richards & Haltiwanger (1982) first synthesized molecular structures in the form of a Möbius ladder, and since then this structure has been of interest in chemistry and chemical stereography,[4] especially in view of the ladder-like form of DNA molecules. With this application in mind, Flapan (1989) studies the mathematical symmetries of embeddings of Möbius ladders in R3.
Möbius ladders have also been used as the shape of a superconducting ring in experiments to study the effects of conductor topology on electron interactions.[5]
Combinatorial optimization
Möbius ladders have also been used in computer science, as part of integer programming approaches to problems of set packing and linear ordering. Certain configurations within these problems can be used to define facets of the polytope describing a linear programming relaxation of the problem; these facets are called Möbius ladder constraints.[6]
See also
Notes
- ^ McSorley (1998).
- ^ Jakobson & Rivin (1999); Valdes (1991).
- ^ Biggs, Damerell & Sands (1972).
- ^ Simon (1992).
- ^ Mila, Stafford & Capponi (1998); Deng, Xu & Liu (2002).
- ^ Bolotashvili, Kovalev & Girlich (1999); Borndörfer & Weismantel (2000); Grötschel, Jünger, and Reinelt (1985a, 1985b); Newman & Vempala (2001)
References
- Biggs, N. L.; Damerell, R. M.; Sands, D. A. (1972). "Recursive families of graphs". Journal of Combinatorial Theory. Series B. 12: 123–131. doi:10.1016/0095-8956(72)90016-0. MR 0294172.
{{cite journal}}: Invalid|ref=harv(help) - Bolotashvili, G.; Kovalev, M.; Girlich, E. (1999). "New facets of the linear ordering polytope". SIAM Journal on Discrete Mathematics. 12 (3): 326–336. doi:10.1137/S0895480196300145. MR 1710240.
{{cite journal}}: Invalid|ref=harv(help) - Borndörfer, Ralf; Weismantel, Robert (2000). "Set packing relaxations of some integer programs". Mathematical Programming. Series A. 88 (3): 425–450. doi:10.1007/PL00011381. MR 1782150.
{{cite journal}}: Invalid|ref=harv(help) - Deng, Wen-Ji; Xu, Ji-Huan; Liu, Ping (2002). "Period halving of persistent currents in mesoscopic Möbius ladders". Chinese Physics Letters. 19 (7): 988–991. arXiv:cond-mat/0209421. doi:10.1088/0256-307X/19/7/333.
{{cite journal}}: Invalid|ref=harv(help) - Flapan, Erica (1989). "Symmetries of Möbius ladders". Mathematische Annalen. 283 (2): 271–283. doi:10.1007/BF01446435. MR 0980598.
{{cite journal}}: Invalid|ref=harv(help) - Grötschel, M.; Jünger, M.; Reinelt, G. (1985a). "On the acyclic subgraph polytope". Mathematical Programming. 33: 28–42. doi:10.1007/BF01582009. MR 0809747.
{{cite journal}}: Invalid|ref=harv(help) - Grötschel, M.; Jünger, M.; Reinelt, G. (1985b). "Facets of the linear ordering polytope". Mathematical Programming. 33: 43–60. doi:10.1007/BF01582010. MR 0809748.
{{cite journal}}: Invalid|ref=harv(help) - Gubser, Bradley S. (1996). "A characterization of almost-planar graphs". Combinatorics, Probability and Computing. 5 (3): 227–245. doi:10.1017/S0963548300002005. MR 1411084.
{{cite journal}}: Invalid|ref=harv(help) - Guy, Richard K.; Harary, Frank (1967). "On the Möbius ladders". Canadian Mathematical Bulletin. 10: 493–496. doi:10.4153/CMB-1967-046-4. MR 0224499.
{{cite journal}}: Invalid|ref=harv(help) - Jakobson, Dmitry; Rivin, Igor (1999). "On some extremal problems in graph theory". arXiv:math.CO/9907050.
{{cite journal}}: Cite journal requires|journal=(help); Invalid|ref=harv(help) - Li, De-ming (2005). "Genus distributions of Möbius ladders". Northeastern Mathematics Journal. 21 (1): 70–80. MR 2124859.
{{cite journal}}: Invalid|ref=harv(help) - Maharry, John (2000). "A characterization of graphs with no cube minor". Journal of Combinatorial Theory. Series B. 80 (2): 179–201. doi:10.1006/jctb.2000.1968. MR 1794690.
{{cite journal}}: Invalid|ref=harv(help) - McSorley, John P. (1998). "Counting structures in the Möbius ladder". Discrete Mathematics. 184 (1–3): 137–164. doi:10.1016/S0012-365X(97)00086-1. MR 1609294.
{{cite journal}}: Invalid|ref=harv(help) - De Mier, Anna; Noy, Marc (2004). "On graphs determined by their Tutte polynomials". Graphs and Combinatorics. 20 (1): 105–119. doi:10.1007/s00373-003-0534-z. MR 2048553.
{{cite journal}}: Invalid|ref=harv(help) - Mila, Frédéric; Stafford, C. A.; Capponi, Sylvain (1998). "Persistent currents in a Möbius ladder: A test of interchain coherence of interacting electrons" (PDF). Physical Review B. 57 (3): 1457–1460. doi:10.1103/PhysRevB.57.1457.
{{cite journal}}: Invalid|ref=harv(help) - Newman, Alantha; Vempala, Santosh (2001). "Fences are futile: on relaxations for the linear ordering problem". Integer Programming and Combinatorial Optimization: 8th International IPCO Conference, Utrecht, The Netherlands, June 13–15, 2001, Proceedings. Lecture Notes in Computer Science. Vol. 2081. Berlin: Springer-Verlag. pp. 333–347. doi:10.1007/3-540-45535-3_26. MR 2041937.
{{cite conference}}: Invalid|ref=harv(help); Unknown parameter|booktitle=ignored (|book-title=suggested) (help) - Simon, Jonathan (1992). "Knots and chemistry". New scientific applications of geometry and topology (Baltimore, MD, 1992). Proceedings of Symposia in Applied Mathematics. Vol. 45. Providence, RI: American Mathematical Society. pp. 97–130. MR 1196717.
{{cite conference}}: Invalid|ref=harv(help); Unknown parameter|booktitle=ignored (|book-title=suggested) (help) - Valdes, L. (1991). "Extremal properties of spanning trees in cubic graphs". Proceedings of the Twenty-second Southeastern Conference on Combinatorics, Graph Theory, and Computing (Baton Rouge, LA, 1991). Congressus Numerantium. Vol. 85. pp. 143–160. MR 1152127.
{{cite conference}}: Invalid|ref=harv(help); Unknown parameter|booktitle=ignored (|book-title=suggested) (help) - Wagner, K. (1937). "Über eine Eigenschaft der ebenen Komplexe". Mathematische Annalen. 114: 570–590. doi:10.1007/BF01594196. MR 1513158.
{{cite journal}}: Invalid|ref=harv(help) - Walba, D.; Richards, R.; Haltiwanger, R. C. (1982). "Total synthesis of the first molecular Möbius strip". Journal of the American Chemical Society. 104 (11): 3219–3221. doi:10.1021/ja00375a051.
{{cite journal}}: Invalid|ref=harv(help)
