Laurent series

| Mathematical analysis → Complex analysis |
| Complex analysis |
|---|
 |
| Complex numbers |
| Complex functions |
| Basic theory |
| Geometric function theory |
| People |
In mathematics, the Laurent series of a complex function is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where a Taylor series expansion cannot be applied. The Laurent series was named after and first published by Pierre Alphonse Laurent in 1843. Karl Weierstrass had previously described it in a paper written in 1841 but not published until 1894.[1]
Definition
[edit]The Laurent series for a complex function about an arbitrary point is given by[2][3] where the coefficients are defined by a contour integral that generalizes Cauchy's integral formula:
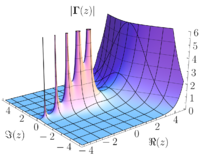
The path of integration is counterclockwise around a Jordan curve enclosing and lying in an annulus in which is holomorphic (analytic). The expansion for will then be valid anywhere inside the annulus. The annulus is shown in red in the figure on the right, along with an example of a suitable path of integration labeled . When is defined as the circle , where , this amounts to computing the complex Fourier coefficients of the restriction of to .[4] The fact that these integrals are unchanged by a deformation of the contour is an immediate consequence of Green's theorem.
One may also obtain the Laurent series for a complex function at . However, this is the same as when .
In practice, the above integral formula may not offer the most practical method for computing the coefficients for a given function ; instead, one often pieces together the Laurent series by combining known Taylor expansions. Because the Laurent expansion of a function is unique whenever it exists, any expression of this form that equals the given function in some annulus must actually be the Laurent expansion of .
Convergence
[edit]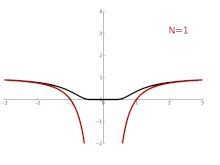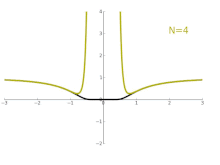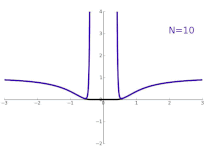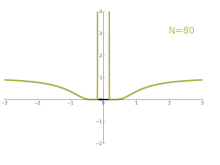
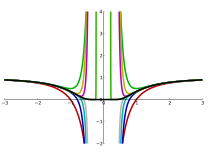
Laurent series with complex coefficients are an important tool in complex analysis, especially to investigate the behavior of functions near singularities.
Consider for instance the function with . As a real function, it is infinitely differentiable everywhere; as a complex function however it is not differentiable at . The Laurent series of is obtained via the power series representation, which converges to for all except at the singularity . The graph on the right shows in black and its Laurent approximations As , the approximation becomes exact for all (complex) numbers except at the singularity .
More generally, Laurent series can be used to express holomorphic functions defined on an annulus, much as power series are used to express holomorphic functions defined on a disc.
Suppose is a given Laurent series with complex coefficients and a complex center . Then there exists a unique inner radius and outer radius such that:
- The Laurent series converges on the open annulus . That is, both the positive- and negative degree power series converge. Furthermore, this convergence will be uniform on compact sets. Finally, the convergent series defines a holomorphic function on .
- Outside the annulus, the Laurent series diverges. That is, at each point in the exterior of , either the positive- or negative degree power series diverges.
- On the boundary of the annulus, one cannot make a general statement, except that there is at least one point on the inner boundary and one point on the outer boundary such that cannot be holomorphically extended to those points; giving rise to a Riemann-Hilbert problem.[5]
It is possible that may be zero or may be infinite; at the other extreme, it's not necessarily true that is less than . These radii can be computed by taking the limit superior of the coefficients such that:
When , the coefficient of the Laurent expansion is called the residue of at the singularity .[6] For example, the function is holomorphic everywhere except at . The Laurent expansion about can then be obtained from the power series representation: hence, the residue is given by .
Conversely, for a holomorphic function defined on the annulus , there always exists a unique Laurent series with center which converges (at least on ) to .
For example, consider the following rational function, along with its partial fraction expansion:
This function has singularities at and , where the denominator is zero and the expression is therefore undefined. A Taylor series about (which yields a power series) will only converge in a disc of radius 1, since it "hits" the singularity at .
However, there are three possible Laurent expansions about 0, depending on the radius of :
- One series is defined on the inner disc where |z| < 1; it is the same as the Taylor series, This follows from the partial fraction form of the function, along with the formula for the sum of a geometric series, for .
- The second series is defined on the middle annulus where is caught between the two singularities: Here, we use the alternative form of the geometric series summation, for .
- The third series is defined on the infinite outer annulus where , (which is also the Laurent expansion at ) This series can be derived using geometric series as before, or by performing polynomial long division of 1 by , not stopping with a remainder but continuing into terms; indeed, the "outer" Laurent series of a rational function is analogous to the decimal form of a fraction. (The "inner" Taylor series expansion can be obtained similarly, just by reversing the term order in the division algorithm.)
Uniqueness
[edit]Suppose a function holomorphic on the annulus has two Laurent series:
Multiply both sides by , where k is an arbitrary integer, and integrate on a path γ inside the annulus,
The series converges uniformly on , where ε is a positive number small enough for γ to be contained in the constricted closed annulus, so the integration and summation can be interchanged. Substituting the identity into the summation yields
Hence the Laurent series is unique.
Laurent polynomials
[edit]A Laurent polynomial is a Laurent series in which only finitely many coefficients are non-zero. Laurent polynomials differ from ordinary polynomials in that they may have terms of negative degree.
Principal part
[edit]The principal part of a Laurent series is the series of terms with negative degree, that is
If the principal part of is a finite sum, then has a pole at of order equal to (negative) the degree of the highest term; on the other hand, if has an essential singularity at , the principal part is an infinite sum (meaning it has infinitely many non-zero terms).
If the inner radius of convergence of the Laurent series for is 0, then has an essential singularity at if and only if the principal part is an infinite sum, and has a pole otherwise.
If the inner radius of convergence is positive, may have infinitely many negative terms but still be regular at , as in the example above, in which case it is represented by a different Laurent series in a disk about .
Laurent series with only finitely many negative terms are well-behaved—they are a power series divided by , and can be analyzed similarly—while Laurent series with infinitely many negative terms have complicated behavior on the inner circle of convergence.
Multiplication and sum
[edit]Laurent series cannot in general be multiplied. Algebraically, the expression for the terms of the product may involve infinite sums which need not converge (one cannot take the convolution of integer sequences). Geometrically, the two Laurent series may have non-overlapping annuli of convergence.
Two Laurent series with only finitely many negative terms can be multiplied: algebraically, the sums are all finite; geometrically, these have poles at , and inner radius of convergence 0, so they both converge on an overlapping annulus.
Thus when defining formal Laurent series, one requires Laurent series with only finitely many negative terms.
Similarly, the sum of two convergent Laurent series need not converge, though it is always defined formally, but the sum of two bounded below Laurent series (or any Laurent series on a punctured disk) has a non-empty annulus of convergence.
Also, for a field , by the sum and multiplication defined above, formal Laurent series would form a field which is also the field of fractions of the ring of formal power series.
See also
[edit]- Puiseux series
- Mittag-Leffler's theorem
- Formal Laurent series – Laurent series considered formally, with coefficients from an arbitrary commutative ring, without regard for convergence, and with only finitely many negative terms, so that multiplication is always defined.
- Z-transform – the special case where the Laurent series is taken about zero has much use in time-series analysis.
- Fourier series – the substitution transforms a Laurent series into a Fourier series, or conversely. This is used in the q-series expansion of the j-invariant.
- Padé approximant – Another technique used when a Taylor series is not viable.
Notes
[edit]- ^ Roy, Ranjan (2012), "§1.5 Appendix: Historical Notes by Ranjan Roy", Complex Analysis: In the Spirit of Lipman Bers, by Rodríguez, Rubí E.; Kra, Irwin; Gilman, Jane P. (2nd ed.), Springer, p. 12, doi:10.1007/978-1-4419-7323-8_1, ISBN 978-1-4419-7322-1 Weierstrass, Karl (1841), "Darstellung einer analytischen Function einer complexen Veränderlichen, deren absoluter Betrag zwischen zwei gegebenen Grenzen liegt" [Representation of an analytical function of a complex variable, whose absolute value lies between two given limits], Mathematische Werke (in German), vol. 1, Berlin: Mayer & Müller (published 1894), pp. 51–66
- ^ Ablowitz & Fokas 2003, p. 128
- ^ Folland, Gerald B. (1992), Fourier analysis and its applications, Pacific Grove, Calif: Wadsworth & Brooks/Cole, p. 395, ISBN 978-0-534-17094-3
- ^ Ablowitz & Fokas 2003, pp. 196–197
- ^ Ablowitz & Fokas 2003, p. 152
- ^ Ablowitz & Fokas 2003, p. 130
References
[edit]- Ablowitz, Mark J.; Fokas, Athanassios S. (2003), Complex Variables, Cambridge University Press, ISBN 978-0-521-53429-1




























































![{\displaystyle F[[x]]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fef5b0ebc9d37ad4cdc4048b314a1832bb0b0a18)