From Wikipedia, the free encyclopedia
Fréchet
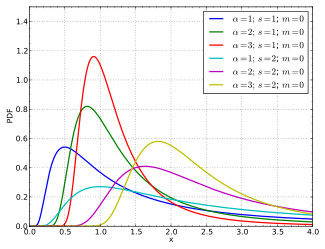
Probability density function
Cumulative distribution function
Parameters
α
∈
(
0
,
∞
)
{\displaystyle \alpha \in (0,\infty )}
shape .
s
∈
(
0
,
∞
)
{\displaystyle s\in (0,\infty )}
scale (default:
s
=
1
{\displaystyle s=1\,}
m
∈
(
−
∞
,
∞
)
{\displaystyle m\in (-\infty ,\infty )}
location of minimum (default:
m
=
0
{\displaystyle m=0\,}
Support
x
>
m
{\displaystyle x>m}
PDF
α
s
(
x
−
m
s
)
−
1
−
α
e
−
(
x
−
m
s
)
−
α
{\displaystyle {\frac {\alpha }{s}}\;\left({\frac {x-m}{s}}\right)^{-1-\alpha }\;e^{-({\frac {x-m}{s}})^{-\alpha }}}
CDF
e
−
(
x
−
m
s
)
−
α
{\displaystyle e^{-({\frac {x-m}{s}})^{-\alpha }}}
Mean
{
m
+
s
Γ
(
1
−
1
α
)
for
α
>
1
∞
otherwise
{\displaystyle {\begin{cases}\ m+s\Gamma \left(1-{\frac {1}{\alpha }}\right)&{\text{for }}\alpha >1\\\ \infty &{\text{otherwise}}\end{cases}}}
Median
m
+
s
log
e
(
2
)
α
{\displaystyle m+{\frac {s}{\sqrt[{\alpha }]{\log _{e}(2)}}}}
Mode
m
+
s
(
α
1
+
α
)
1
/
α
{\displaystyle m+s\left({\frac {\alpha }{1+\alpha }}\right)^{1/\alpha }}
Variance
{
s
2
(
Γ
(
1
−
2
α
)
−
(
Γ
(
1
−
1
α
)
)
2
)
for
α
>
2
∞
otherwise
{\displaystyle {\begin{cases}\ s^{2}\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\left(\Gamma \left(1-{\frac {1}{\alpha }}\right)\right)^{2}\right)&{\text{for }}\alpha >2\\\ \infty &{\text{otherwise}}\end{cases}}}
Skewness
{
Γ
(
1
−
3
α
)
−
3
Γ
(
1
−
2
α
)
Γ
(
1
−
1
α
)
+
2
Γ
3
(
1
−
1
α
)
(
Γ
(
1
−
2
α
)
−
Γ
2
(
1
−
1
α
)
)
3
for
α
>
3
∞
otherwise
{\displaystyle {\begin{cases}\ {\frac {\Gamma \left(1-{\frac {3}{\alpha }}\right)-3\Gamma \left(1-{\frac {2}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+2\Gamma ^{3}\left(1-{\frac {1}{\alpha }}\right)}{\sqrt {\left(\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right)^{3}}}}&{\text{for }}\alpha >3\\\ \infty &{\text{otherwise}}\end{cases}}}
Excess kurtosis
{
−
6
+
Γ
(
1
−
4
α
)
−
4
Γ
(
1
−
3
α
)
Γ
(
1
−
1
α
)
+
3
Γ
2
(
1
−
2
α
)
[
Γ
(
1
−
2
α
)
−
Γ
2
(
1
−
1
α
)
]
2
for
α
>
4
∞
otherwise
{\displaystyle {\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{for }}\alpha >4\\\ \infty &{\text{otherwise}}\end{cases}}}
Entropy
1
+
γ
α
+
γ
+
ln
(
s
α
)
{\displaystyle 1+{\frac {\gamma }{\alpha }}+\gamma +\ln \left({\frac {s}{\alpha }}\right)}
γ
{\displaystyle \gamma }
Euler–Mascheroni constant . MGF
[ 1]
k
{\displaystyle k}
α
>
k
{\displaystyle \alpha >k}
CF
[ 1]
The Fréchet distribution is a special case of the generalized extreme value distribution . It has the cumulative distribution function
Pr
(
X
≤
x
)
=
e
−
x
−
α
if
x
>
0.
{\displaystyle \Pr(X\leq x)=e^{-x^{-\alpha }}{\text{ if }}x>0.}
where α >0 is a shape parameter . It can be generalised to include a location parameter m (the minimum) and a scale parameter s >0 with the cumulative distribution function
Pr
(
X
≤
x
)
=
e
−
(
x
−
m
s
)
−
α
if
x
>
m
.
{\displaystyle \Pr(X\leq x)=e^{-\left({\frac {x-m}{s}}\right)^{-\alpha }}{\text{ if }}x>m.}
Named for Maurice Fréchet who wrote a related paper in 1927, further work was done by Fisher and Tippett in 1928 and by Gumbel in 1958
Characteristics
The single parameter Fréchet with parameter
α
{\displaystyle \alpha }
standardized moment
μ
k
=
∫
0
∞
x
k
f
(
x
)
d
x
=
∫
0
∞
t
−
k
α
e
−
t
d
t
{\displaystyle \mu _{k}=\int _{0}^{\infty }x^{k}f(x)dx=\int _{0}^{\infty }t^{-{\frac {k}{\alpha }}}e^{-t}dt}
(with
t
=
x
−
α
{\displaystyle t=x^{-\alpha }}
k
<
α
{\displaystyle k<\alpha }
μ
k
=
Γ
(
1
−
k
α
)
{\displaystyle \mu _{k}=\Gamma \left(1-{\frac {k}{\alpha }}\right)}
where
Γ
(
z
)
{\displaystyle \Gamma \left(z\right)}
Gamma function .
In particular:
For
α
>
1
{\displaystyle \alpha >1}
expectation is
E
[
X
]
=
Γ
(
1
−
1
α
)
{\displaystyle E[X]=\Gamma (1-{\tfrac {1}{\alpha }})}
For
α
>
2
{\displaystyle \alpha >2}
variance is
Var
(
X
)
=
Γ
(
1
−
2
α
)
−
(
Γ
(
1
−
1
α
)
)
2
{\displaystyle {\text{Var}}(X)=\Gamma (1-{\tfrac {2}{\alpha }})-{\big (}\Gamma (1-{\tfrac {1}{\alpha }}){\big )}^{2}}
The quantile
q
y
{\displaystyle q_{y}}
y
{\displaystyle y}
q
y
=
F
−
1
(
y
)
=
(
−
log
e
y
)
−
1
α
{\displaystyle q_{y}=F^{-1}(y)=\left(-\log _{e}y\right)^{-{\frac {1}{\alpha }}}}
In particular the median is:
q
1
/
2
=
(
log
e
2
)
−
1
α
{\displaystyle q_{1/2}=(\log _{e}2)^{-{\frac {1}{\alpha }}}}
The mode of the distribution is
(
α
α
+
1
)
1
α
{\displaystyle \left({\frac {\alpha }{\alpha +1}}\right)^{\frac {1}{\alpha }}}
Especially for the 3-parameter Fréchet, the first quartile is
q
1
=
m
+
s
log
(
4
)
α
{\displaystyle q_{1}=m+{\frac {s}{\sqrt[{\alpha }]{\log(4)}}}}
q
3
=
m
+
s
log
(
4
3
)
α
{\displaystyle q_{3}=m+{\frac {s}{\sqrt[{\alpha }]{\log({\frac {4}{3}})}}}}
Also the quantiles for the mean and mode are:
F
(
m
e
a
n
)
=
exp
(
−
Γ
−
α
(
1
−
1
α
)
)
{\displaystyle F(mean)=\exp \left(-\Gamma ^{-\alpha }\left(1-{\frac {1}{\alpha }}\right)\right)}
F
(
m
o
d
e
)
=
exp
(
−
α
+
1
α
)
{\displaystyle F(mode)=\exp \left(-{\frac {\alpha +1}{\alpha }}\right)}
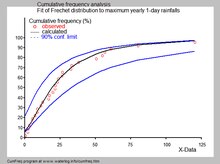
Fitted cumulative Fréchet distribution to extreme one-day rainfalls
Applications
In hydrology , the Fréchet distribution is applied to extreme events such as annually maximum one-day rainfalls and river discharges.[ 2] Oman showing also the 90% confidence belt based on the binomial distribution . The cumulative frequencies of the rainfall data are represented by plotting positions as part of the cumulative frequency analysis . However, in most hydrological applications, the distribution fitting is via the generalized extreme value distribution as this avoids imposing the assumption that the distribution does not have an upper bound (as required by the Frechet distribution when applied to annual maxima). [citation needed
If
X
∼
U
(
0
,
1
)
{\displaystyle X\sim U(0,1)\,}
Uniform distribution (continuous) ) then
m
+
s
(
−
log
(
X
)
)
−
1
/
α
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle m+s(-\log(X))^{-1/\alpha }\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
If
X
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle X\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
k
X
+
b
∼
Frechet
(
α
,
k
s
,
k
m
+
b
)
{\displaystyle kX+b\sim {\textrm {Frechet}}(\alpha ,ks,km+b)\,}
If
X
i
=
Frechet
(
α
,
s
,
m
)
{\displaystyle X_{i}={\textrm {Frechet}}(\alpha ,s,m)\,}
Y
=
max
{
X
1
,
…
,
X
n
}
{\displaystyle Y=\max\{\,X_{1},\ldots ,X_{n}\,\}\,}
Y
∼
Frechet
(
α
,
n
1
α
s
,
m
)
{\displaystyle Y\sim {\textrm {Frechet}}(\alpha ,n^{\tfrac {1}{\alpha }}s,m)\,}
The cumulative distribution function of the Frechet distribution solves the maximum stability postulate equation
If
X
∼
Weibull
(
k
=
α
,
λ
=
m
)
{\displaystyle X\sim {\textrm {Weibull}}(k=\alpha ,\lambda =m)\,}
Weibull distribution ) then
m
2
X
∼
Frechet
(
α
,
s
,
m
)
{\displaystyle {\tfrac {m^{2}}{X}}\sim {\textrm {Frechet}}(\alpha ,s,m)\,}
Properties
See also
References
^ a b Muraleedharan. G, C. Guedes Soares and Cláudia Lucas (2011). "Characteristic and Moment Generating Functions of Generalised Extreme Value Distribution (GEV)". In Linda. L. Wright (Ed.), Sea Level Rise, Coastal Engineering, Shorelines and Tides , Chapter-14, pp. 269-276. Nova Science Publishers. ISBN 978-1-61728-655-1
^ Coles, Stuart (2001). An Introduction to Statistical Modeling of Extreme Values, ISBN 1-85233-459-2
Publications
Fréchet, M., (1927). "Sur la loi de probabilité de l'écart maximum." Ann. Soc. Polon. Math. 6, 93.
Fisher, R.A., Tippett, L.H.C., (1928). "Limiting forms of the frequency distribution of the largest and smallest member of a sample." Proc. Cambridge Philosophical Society 24:180–190.
Gumbel, E.J. (1958). "Statistics of Extremes." Columbia University Press, New York.
Kotz, S.;Nadarajah, S. (2000) Extreme value distributions: theory and applications , World Scientific. ISBN 1860942245
External links
Discrete
with finite with infinite
Continuous
supported on a supported on a supported with support
Mixed
Multivariate Directional Degenerate singular Families











![{\displaystyle m+{\frac {s}{\sqrt[{\alpha }]{\log _{e}(2)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31a72ce4ea6fe77d9c68731c0cafb36bf93dca71)



![{\displaystyle {\begin{cases}\ -6+{\frac {\Gamma \left(1-{\frac {4}{\alpha }}\right)-4\Gamma \left(1-{\frac {3}{\alpha }}\right)\Gamma \left(1-{\frac {1}{\alpha }}\right)+3\Gamma ^{2}\left(1-{\frac {2}{\alpha }}\right)}{\left[\Gamma \left(1-{\frac {2}{\alpha }}\right)-\Gamma ^{2}\left(1-{\frac {1}{\alpha }}\right)\right]^{2}}}&{\text{for }}\alpha >4\\\ \infty &{\text{otherwise}}\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f0e101297df7d5cbc11a6a96d305a162371856d)













![{\displaystyle E[X]=\Gamma (1-{\tfrac {1}{\alpha }})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c4f4b1a753eff200f2ff93b89d1401ebf10652d6)







![{\displaystyle q_{1}=m+{\frac {s}{\sqrt[{\alpha }]{\log(4)}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/72285aecb7128d3dda2842d57a231f1a2f695cef)
![{\displaystyle q_{3}=m+{\frac {s}{\sqrt[{\alpha }]{\log({\frac {4}{3}})}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/43a82679e86feb16cd3ca1d3d9081b9284f3b1d6)










