Transparency and translucency

In the field of optics, transparency (also called pellucidity or diaphaneity) is the physical property of allowing light to pass through the material without appreciable scattering of light. On a macroscopic scale (one in which the dimensions are much larger than the wavelengths of the photons in question), the photons can be said to follow Snell's law. Translucency (also called translucence or translucidity) allows light to pass through but does not necessarily (again, on the macroscopic scale) follow Snell's law; the photons can be scattered at either of the two interfaces, or internally, where there is a change in the index of refraction. In other words, a translucent material is made up of components with different indices of refraction. A transparent material is made up of components with a uniform index of refraction.[1] Transparent materials appear clear, with the overall appearance of one color, or any combination leading up to a brilliant spectrum of every color. The opposite property of translucency is opacity. Other categories of visual appearance, related to the perception of regular or diffuse reflection and transmission of light, have been organized under the concept of cesia in an order system with three variables, including transparency, translucency and opacity among the involved aspects.
When light encounters a material, it can interact with it in several different ways. These interactions depend on the wavelength of the light and the nature of the material. Photons interact with an object by some combination of reflection, absorption and transmission. Some materials, such as plate glass and clean water, transmit much of the light that falls on them and reflect little of it; such materials are called optically transparent. Many liquids and aqueous solutions are highly transparent. Absence of structural defects (voids, cracks, etc.) and molecular structure of most liquids are mostly responsible for excellent optical transmission.
Materials that do not transmit light are called opaque. Many such substances have a chemical composition which includes what are referred to as absorption centers. Many substances are selective in their absorption of white light frequencies. They absorb certain portions of the visible spectrum while reflecting others. The frequencies of the spectrum which are not absorbed are either reflected or transmitted for our physical observation. This is what gives rise to color. The attenuation of light of all frequencies and wavelengths is due to the combined mechanisms of absorption and scattering.[2]
Transparency can provide almost perfect camouflage for animals able to achieve it. This is easier in dimly-lit or turbid seawater than in good illumination. Many marine animals such as jellyfish are highly transparent.

Etymology
[edit]- late Middle English: from Old French, from medieval Latin transparent- 'visible through', from Latin transparere, from trans- 'through' + parere 'be visible'.[citation needed]
- late 16th century (in the Latin sense): from Latin translucent- 'shining through', from the verb translucere, from trans- 'through' + lucere 'to shine'.[citation needed]
- late Middle English opake, from Latin opacus 'darkened'. The current spelling (rare before the 19th century) has been influenced by the French form.[citation needed]
Introduction
[edit]This section needs additional citations for verification. (April 2021) |
With regard to the absorption of light, primary material considerations include:
- At the electronic level, absorption in the ultraviolet and visible (UV-Vis) portions of the spectrum depends on whether the electron orbitals are spaced (or "quantized") such that electrons can absorb a quantum of light (or photon) of a specific frequency. For example, in most glasses, electrons have no available energy levels above them in the range of that associated with visible light, or if they do, the transition to them would violate selection rules, meaning there is no appreciable absorption in pure (undoped) glasses, making them ideal transparent materials for windows in buildings.
- At the atomic or molecular level, physical absorption in the infrared portion of the spectrum depends on the frequencies of atomic or molecular vibrations or chemical bonds, and on selection rules. Nitrogen and oxygen are not greenhouse gases because there is no molecular dipole moment.
With regard to the scattering of light, the most critical factor is the length scale of any or all of these structural features relative to the wavelength of the light being scattered. Primary material considerations include:
- Crystalline structure: whether the atoms or molecules exhibit the 'long-range order' evidenced in crystalline solids.
- Glassy structure: Scattering centers include fluctuations in density or composition.
- Microstructure: Scattering centers include internal surfaces such as grain boundaries, crystallographic defects, and microscopic pores.
- Organic materials: Scattering centers include fiber and cell structures and boundaries.
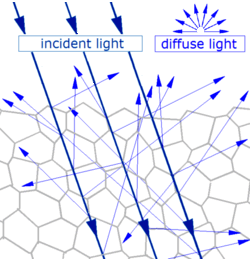
Diffuse reflection - Generally, when light strikes the surface of a (non-metallic and non-glassy) solid material, it bounces off in all directions due to multiple reflections by the microscopic irregularities inside the material (e.g., the grain boundaries of a polycrystalline material or the cell or fiber boundaries of an organic material), and by its surface, if it is rough. Diffuse reflection is typically characterized by omni-directional reflection angles. Most of the objects visible to the naked eye are identified via diffuse reflection. Another term commonly used for this type of reflection is "light scattering". Light scattering from the surfaces of objects is our primary mechanism of physical observation.[3][4]
Light scattering in liquids and solids depends on the wavelength of the light being scattered. Limits to spatial scales of visibility (using white light) therefore arise, depending on the frequency of the light wave and the physical dimension (or spatial scale) of the scattering center. Visible light has a wavelength scale on the order of 0.5 μm. Scattering centers (or particles) as small as 1 μm have been observed directly in the light microscope (e.g., Brownian motion).[5][6]
Transparent ceramics
[edit]Optical transparency in polycrystalline materials is limited by the amount of light scattered by their microstructural features. Light scattering depends on the wavelength of the light. Limits to spatial scales of visibility (using white light) therefore arise, depending on the frequency of the light wave and the physical dimension of the scattering center. For example, since visible light has a wavelength scale on the order of a micrometre, scattering centers will have dimensions on a similar spatial scale. Primary scattering centers in polycrystalline materials include microstructural defects such as pores and grain boundaries. In addition to pores, most of the interfaces in a typical metal or ceramic object are in the form of grain boundaries, which separate tiny regions of crystalline order. When the size of the scattering center (or grain boundary) is reduced below the size of the wavelength of the light being scattered, the scattering no longer occurs to any significant extent.
In the formation of polycrystalline materials (metals and ceramics) the size of the crystalline grains is determined largely by the size of the crystalline particles present in the raw material during formation (or pressing) of the object. Moreover, the size of the grain boundaries scales directly with particle size. Thus, a reduction of the original particle size well below the wavelength of visible light (about 1/15 of the light wavelength, or roughly 600 nm / 15 = 40 nm) eliminates much of the light scattering, resulting in a translucent or even transparent material.
Computer modeling of light transmission through translucent ceramic alumina has shown that microscopic pores trapped near grain boundaries act as primary scattering centers. The volume fraction of porosity had to be reduced below 1% for high-quality optical transmission (99.99 percent of theoretical density). This goal has been readily accomplished and amply demonstrated in laboratories and research facilities worldwide using the emerging chemical processing methods encompassed by the methods of sol-gel chemistry and nanotechnology.[7]

Transparent ceramics have created interest in their applications for high energy lasers, transparent armor windows, nose cones for heat seeking missiles, radiation detectors for non-destructive testing, high energy physics, space exploration, security and medical imaging applications. Large laser elements made from transparent ceramics can be produced at a relatively low cost. These components are free of internal stress or intrinsic birefringence, and allow relatively large doping levels or optimized custom-designed doping profiles. This makes ceramic laser elements particularly important for high-energy lasers.
The development of transparent panel products will have other potential advanced applications including high strength, impact-resistant materials that can be used for domestic windows and skylights. Perhaps more important is that walls and other applications will have improved overall strength, especially for high-shear conditions found in high seismic and wind exposures. If the expected improvements in mechanical properties bear out, the traditional limits seen on glazing areas in today's building codes could quickly become outdated if the window area actually contributes to the shear resistance of the wall.
Currently available infrared transparent materials typically exhibit a trade-off between optical performance, mechanical strength and price. For example, sapphire (crystalline alumina) is very strong, but it is expensive and lacks full transparency throughout the 3–5 μm mid-infrared range. Yttria is fully transparent from 3–5 μm, but lacks sufficient strength, hardness, and thermal shock resistance for high-performance aerospace applications. A combination of these two materials in the form of the yttrium aluminium garnet (YAG) is one of the top performers in the field.[citation needed]
Absorption of light in solids
[edit]This section needs additional citations for verification. (April 2021) |
When light strikes an object, it usually has not just a single frequency (or wavelength) but many. Objects have a tendency to selectively absorb, reflect, or transmit light of certain frequencies. That is, one object might reflect green light while absorbing all other frequencies of visible light. Another object might selectively transmit blue light while absorbing all other frequencies of visible light. The manner in which visible light interacts with an object is dependent upon the frequency of the light, the nature of the atoms in the object, and often, the nature of the electrons in the atoms of the object.
Some materials allow much of the light that falls on them to be transmitted through the material without being reflected. Materials that allow the transmission of light waves through them are called optically transparent. Chemically pure (undoped) window glass and clean river or spring water are prime examples of this.
Materials that do not allow the transmission of any light wave frequencies are called opaque. Such substances may have a chemical composition which includes what are referred to as absorption centers. Most materials are composed of materials that are selective in their absorption of light frequencies. Thus they absorb only certain portions of the visible spectrum. The frequencies of the spectrum which are not absorbed are either reflected back or transmitted for our physical observation. In the visible portion of the spectrum, this is what gives rise to color.[8][9]
Absorption centers are largely responsible for the appearance of specific wavelengths of visible light all around us. Moving from longer (0.7 μm) to shorter (0.4 μm) wavelengths: Red, orange, yellow, green, and blue (ROYGB) can all be identified by our senses in the appearance of color by the selective absorption of specific light wave frequencies (or wavelengths). Mechanisms of selective light wave absorption include:
- Electronic: Transitions in electron energy levels within the atom (e.g., pigments). These transitions are typically in the ultraviolet (UV) and/or visible portions of the spectrum.
- Vibrational: Resonance in atomic/molecular vibrational modes. These transitions are typically in the infrared portion of the spectrum.
UV-Vis: electronic transitions
[edit]In electronic absorption, the frequency of the incoming light wave is at or near the energy levels of the electrons within the atoms that compose the substance. In this case, the electrons will absorb the energy of the light wave and increase their energy state, often moving outward from the nucleus of the atom into an outer shell or orbital.
The atoms that bind together to make the molecules of any particular substance contain a number of electrons (given by the atomic number Z in the periodic table). Recall that all light waves are electromagnetic in origin. Thus they are affected strongly when coming into contact with negatively charged electrons in matter. When photons (individual packets of light energy) come in contact with the valence electrons of an atom, one of several things can and will occur:
- A molecule absorbs the photon, some of the energy may be lost via luminescence, fluorescence and phosphorescence.
- A molecule absorbs the photon, which results in reflection or scattering.
- A molecule cannot absorb the energy of the photon and the photon continues on its path. This results in transmission (provided no other absorption mechanisms are active).
Most of the time, it is a combination of the above that happens to the light that hits an object. The states in different materials vary in the range of energy that they can absorb. Most glasses, for example, block ultraviolet (UV) light. What happens is the electrons in the glass absorb the energy of the photons in the UV range while ignoring the weaker energy of photons in the visible light spectrum. But there are also existing special glass types, like special types of borosilicate glass or quartz that are UV-permeable and thus allow a high transmission of ultraviolet light.
Thus, when a material is illuminated, individual photons of light can make the valence electrons of an atom transition to a higher electronic energy level. The photon is destroyed in the process and the absorbed radiant energy is transformed to electric potential energy. Several things can happen, then, to the absorbed energy: It may be re-emitted by the electron as radiant energy (in this case, the overall effect is in fact a scattering of light), dissipated to the rest of the material (i.e., transformed into heat), or the electron can be freed from the atom (as in the photoelectric effects and Compton effects).
Infrared: bond stretching
[edit]
The primary physical mechanism for storing mechanical energy of motion in condensed matter is through heat, or thermal energy. Thermal energy manifests itself as energy of motion. Thus, heat is motion at the atomic and molecular levels. The primary mode of motion in crystalline substances is vibration. Any given atom will vibrate around some mean or average position within a crystalline structure, surrounded by its nearest neighbors. This vibration in two dimensions is equivalent to the oscillation of a clock's pendulum. It swings back and forth symmetrically about some mean or average (vertical) position. Atomic and molecular vibrational frequencies may average on the order of 1012 cycles per second (Terahertz radiation).
When a light wave of a given frequency strikes a material with particles having the same or (resonant) vibrational frequencies, those particles will absorb the energy of the light wave and transform it into thermal energy of vibrational motion. Since different atoms and molecules have different natural frequencies of vibration, they will selectively absorb different frequencies (or portions of the spectrum) of infrared light. Reflection and transmission of light waves occur because the frequencies of the light waves do not match the natural resonant frequencies of vibration of the objects. When infrared light of these frequencies strikes an object, the energy is reflected or transmitted.
If the object is transparent, then the light waves are passed on to neighboring atoms through the bulk of the material and re-emitted on the opposite side of the object. Such frequencies of light waves are said to be transmitted.[10][11]
Transparency in insulators
[edit]An object may be not transparent either because it reflects the incoming light or because it absorbs the incoming light. Almost all solids reflect a part and absorb a part of the incoming light.
When light falls onto a block of metal, it encounters atoms that are tightly packed in a regular lattice and a "sea of electrons" moving randomly between the atoms.[12] In metals, most of these are non-bonding electrons (or free electrons) as opposed to the bonding electrons typically found in covalently bonded or ionically bonded non-metallic (insulating) solids. In a metallic bond, any potential bonding electrons can easily be lost by the atoms in a crystalline structure. The effect of this delocalization is simply to exaggerate the effect of the "sea of electrons". As a result of these electrons, most of the incoming light in metals is reflected back, which is why we see a shiny metal surface.
Most insulators (or dielectric materials) are held together by ionic bonds. Thus, these materials do not have free conduction electrons, and the bonding electrons reflect only a small fraction of the incident wave. The remaining frequencies (or wavelengths) are free to propagate (or be transmitted). This class of materials includes all ceramics and glasses.
If a dielectric material does not include light-absorbent additive molecules (pigments, dyes, colorants), it is usually transparent to the spectrum of visible light. Color centers (or dye molecules, or "dopants") in a dielectric absorb a portion of the incoming light. The remaining frequencies (or wavelengths) are free to be reflected or transmitted. This is how colored glass is produced.
Most liquids and aqueous solutions are highly transparent. For example, water, cooking oil, rubbing alcohol, air, and natural gas are all clear. Absence of structural defects (voids, cracks, etc.) and molecular structure of most liquids are chiefly responsible for their excellent optical transmission. The ability of liquids to "heal" internal defects via viscous flow is one of the reasons why some fibrous materials (e.g., paper or fabric) increase their apparent transparency when wetted. The liquid fills up numerous voids making the material more structurally homogeneous.[citation needed]
Light scattering in an ideal defect-free crystalline (non-metallic) solid that provides no scattering centers for incoming light will be due primarily to any effects of anharmonicity within the ordered lattice. Light transmission will be highly directional due to the typical anisotropy of crystalline substances, which includes their symmetry group and Bravais lattice. For example, the seven different crystalline forms of quartz silica (silicon dioxide, SiO2) are all clear, transparent materials.[13]
Optical waveguides
[edit]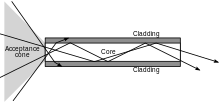

Optically transparent materials focus on the response of a material to incoming light waves of a range of wavelengths. Guided light wave transmission via frequency selective waveguides involves the emerging field of fiber optics and the ability of certain glassy compositions to act as a transmission medium for a range of frequencies simultaneously (multi-mode optical fiber) with little or no interference between competing wavelengths or frequencies. This resonant mode of energy and data transmission via electromagnetic (light) wave propagation is relatively lossless.[citation needed]
An optical fiber is a cylindrical dielectric waveguide that transmits light along its axis by the process of total internal reflection. The fiber consists of a core surrounded by a cladding layer. To confine the optical signal in the core, the refractive index of the core must be greater than that of the cladding. The refractive index is the parameter reflecting the speed of light in a material. (Refractive index is the ratio of the speed of light in vacuum to the speed of light in a given medium. The refractive index of vacuum is therefore 1.) The larger the refractive index, the more slowly light travels in that medium. Typical values for core and cladding of an optical fiber are 1.48 and 1.46, respectively.[citation needed]
When light traveling in a dense medium hits a boundary at a steep angle, the light will be completely reflected. This effect, called total internal reflection, is used in optical fibers to confine light in the core. Light travels along the fiber bouncing back and forth off of the boundary. Because the light must strike the boundary with an angle greater than the critical angle, only light that enters the fiber within a certain range of angles will be propagated. This range of angles is called the acceptance cone of the fiber. The size of this acceptance cone is a function of the refractive index difference between the fiber's core and cladding. Optical waveguides are used as components in integrated optical circuits (e.g., combined with lasers or light-emitting diodes, LEDs) or as the transmission medium in local and long-haul optical communication systems.[citation needed]
Mechanisms of attenuation
[edit]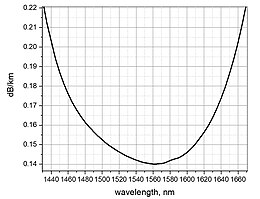
Attenuation in fiber optics, also known as transmission loss, is the reduction in intensity of the light beam (or signal) with respect to distance traveled through a transmission medium. It is an important factor limiting the transmission of a signal across large distances. Attenuation coefficients in fiber optics usually use units of dB/km through the medium due to the very high quality of transparency of modern optical transmission media. The medium is usually a fiber of silica glass that confines the incident light beam to the inside.
In optical fibers, the main source of attenuation is scattering from molecular level irregularities, called Rayleigh scattering,[15] due to structural disorder and compositional fluctuations of the glass structure. This same phenomenon is seen as one of the limiting factors in the transparency of infrared missile domes.[16] Further attenuation is caused by light absorbed by residual materials, such as metals or water ions, within the fiber core and inner cladding. Light leakage due to bending, splices, connectors, or other outside forces are other factors resulting in attenuation. At high optical powers, scattering can also be caused by nonlinear optical processes in the fiber.[17]
As camouflage
[edit]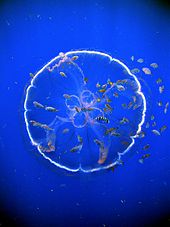
Many marine animals that float near the surface are highly transparent, giving them almost perfect camouflage.[18] However, transparency is difficult for bodies made of materials that have different refractive indices from seawater. Some marine animals such as jellyfish have gelatinous bodies, composed mainly of water; their thick mesogloea is acellular and highly transparent. This conveniently makes them buoyant, but it also makes them large for their muscle mass, so they cannot swim fast, making this form of camouflage a costly trade-off with mobility.[18] Gelatinous planktonic animals are between 50 and 90 percent transparent. A transparency of 50 percent is enough to make an animal invisible to a predator such as cod at a depth of 650 metres (2,130 ft); better transparency is required for invisibility in shallower water, where the light is brighter and predators can see better. For example, a cod can see prey that are 98 percent transparent in optimal lighting in shallow water. Therefore, sufficient transparency for camouflage is more easily achieved in deeper waters.[18] For the same reason, transparency in air is even harder to achieve, but a partial example is found in the glass frogs of the South American rain forest, which have translucent skin and pale greenish limbs.[19] Several Central American species of clearwing (ithomiine) butterflies and many dragonflies and allied insects also have wings which are mostly transparent, a form of crypsis that provides some protection from predators.[citation needed]
See also
[edit]References
[edit]- ^ Thomas, S. M. (October 21, 1999). "What determines whether a substance is transparent?". Scientific American.
- ^ Fox, M. (2002). Optical Properties of Solids. Oxford University Press.
- ^ Kerker, M. (1969). The Scattering of Light. Academic, New York.
- ^ Mandelstam, L.I. (1926). "Light Scattering by Inhomogeneous Media". Zh. Russ. Fiz-Khim. Ova. 58: 381.
- ^ van de Hulst, H.C. (1981). Light scattering by small particles. New York: Dover. ISBN 0-486-64228-3.
- ^ Bohren, C.F. & Huffmann, D.R. (1983). Absorption and scattering of light by small particles. New York: Wiley.
- ^ Yamashita, I.; et al. (2008). "Transparent Ceramics". J. Am. Ceram. Soc. 91 (3): 813. doi:10.1111/j.1551-2916.2007.02202.x.
- ^ Simmons, J. & Potter, K.S. (2000). Optical Materials. Academic Press.
- ^ Uhlmann, D.R.; et al. (1991). Optical Properties of Glass. Amer. Ceram. Soc.
- ^ Gunzler, H. & Gremlich, H. (2002). IR Spectroscopy: An Introduction. Wiley.
- ^ Stuart, B. (2004). Infrared Spectroscopy: Fundamentals and Applications. Wiley.
- ^ Mott, N.F. & Jones, H. Theory of the Properties of Metals and Alloys. Clarendon Press, Oxford (1936) Dover Publications (1958).
- ^ Griffin, A. (1968). "Brillouin Light Scattering from Crystals in the Hydrodynamic Region". Rev. Mod. Phys. 40 (1): 167. Bibcode:1968RvMP...40..167G. doi:10.1103/RevModPhys.40.167.
- ^ Khrapko, R.; Logunov, S. L.; Li, M.; Matthews, H. B.; Tandon, P.; Zhou, C. (2024-04-15). "Quasi Single-Mode Fiber With Record-Low Attenuation of 0.1400 dB/km". IEEE Photonics Technology Letters. 36 (8): 539–542. Bibcode:2024IPTL...36..539K. doi:10.1109/LPT.2024.3372786. ISSN 1041-1135.
- ^ I. P. Kaminow, T. Li (2002), Optical fiber telecommunications IV, Vol. 1, p. 223 Archived 2013-05-27 at the Wayback Machine
- ^ Archibald, P.S. & Bennett, H.E. (1978). Benton, Stephen A. & Knight, Geoffery (eds.). "Scattering from infrared missile domes". Opt. Eng. Optics in Missile Engineering. 17: 647. Bibcode:1978SPIE..133...71A. doi:10.1117/12.956078. S2CID 173179565.
- ^ Smith, R.G. (1972). "Optical power handling capacity of low loss optical fibers as determined by stimulated Raman and Brillouin scattering". Appl. Opt. 11 (11): 2489–94. Bibcode:1972ApOpt..11.2489S. doi:10.1364/AO.11.002489. PMID 20119362.
- ^ a b c Herring, Peter (2002). The Biology of the Deep Ocean. Oxford University Press. ISBN 978-0-19-854956-7. pp. 190–191.
- ^ Naish, D. "Green-boned glass frogs, monkey frogs, toothless toads". Tetrapod zoology. scienceblogs.com. Archived from the original on 11 November 2012. Retrieved 14 February 2013.
Further reading
[edit]- Electrodynamics of continuous media, Landau, L. D., Lifshits. E.M. and Pitaevskii, L.P., (Pergamon Press, Oxford, 1984)
- Laser Light Scattering: Basic Principles and Practice Chu, B., 2nd Edn. (Academic Press, New York 1992)
- Solid State Laser Engineering, W. Koechner (Springer-Verlag, New York, 1999)
- Introduction to Chemical Physics, J.C. Slater (McGraw-Hill, New York, 1939)
- Modern Theory of Solids, F. Seitz, (McGraw-Hill, New York, 1940)
- Modern Aspects of the Vitreous State, J.D.MacKenzie, Ed. (Butterworths, London, 1960)
