Pareto principle

For the optimal allocation of resources, see Pareto efficiency.

The Pareto principle may apply to fundraising, i.e. 20% of the donors contributing towards 80% of the total.

The Pareto principle (also known as the 80/20 rule, the law of the vital few and the principle of factor sparsity) states that for many outcomes, roughly 80% of consequences come from 20% of causes (the "vital few").

In 1941, management consultant Joseph M. Juran developed the concept in the context of quality control and improvement after reading the works of Italian sociologist and economist Vilfredo Pareto, who wrote in 1906 about the 80/20 connection while teaching at the University of Lausanne. In his first work, Cours d'économie politique, Pareto showed that approximately 80% of the land in the Kingdom of Italy was owned by 20% of the population. The Pareto principle is only tangentially related to the Pareto efficiency.

Mathematically, the 80/20 rule is roughly described by a power law distribution (also known as a Pareto distribution) for a particular set of parameters. Many natural phenomena are distributed according to power law statistics. It is an adage of business management that "80% of sales come from 20% of clients."

History

In 1941, Joseph M. Juran, a Romanian-born American engineer, came across the work of Italian polymath Vilfredo Pareto. Pareto noted that approximately 80% of Italy's land was owned by 20% of the population. Juran applied the observation that 80% of an issue is caused by 20% of the causes to quality issues. Later during his career, Juran preferred to describe this as "the vital few and the useful many" to highlight that the contribution of the remaining 80% should not be discarded entirely.

Mathematical explanation

The demonstration of the Pareto principle is explained by a large proportion of process variation being associated with a small proportion of process variables. This is a special case of the wider phenomenon of Pareto distributions. If the Pareto index α, which is one of the parameters characterizing a Pareto distribution, is chosen as α = log₄5 ≈ 1.16, then one has 80% of effects coming from 20% of causes.

The term 80/20 is only a shorthand for the general principle at work. In individual cases, the distribution could be nearer to 90/10 or 70/30. There is also no need for the two numbers to add up to the number 100, as they are measures of different things. The Pareto principle is an illustration of a "power law" relationship, which also occurs in phenomena such as bush fires and earthquakes. Because it is self-similar over a wide range of magnitudes, it produces outcomes completely different from Normal or Gaussian distribution phenomena. This fact explains the frequent breakdowns of sophisticated financial instruments, which are modeled on the assumption that a Gaussian relationship is appropriate to something like stock price movements.

Gini coefficient and Hoover index

Using the "A:B" notation (for example, 0.8:0.2) and with A + B = 1, inequality measures like the Gini index (G) and the Hoover index (H) can be computed. In this case both are the same:

$H=G=|2A-1|=|1-2B|\,$

$A:B=\left({\frac {1+H}{2}}\right):\left({\frac {1-H}{2}}\right)$

Analysis

A Pareto analysis in a diagram showing which cause should be addressed first

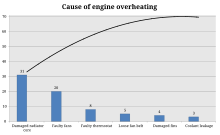
Pareto analysis is a formal technique useful where many possible courses of action are competing for attention. In essence, the problem-solver estimates the benefit delivered by each action, then selects a number of the most effective actions that deliver a total benefit reasonably close to the maximal possible one.

Pareto analysis is a creative way of looking at causes of problems because it helps stimulate thinking and organize thoughts. However, it can be limited by its exclusion of possibly important problems which may be small initially, but will grow with time. It should be combined with other analytical tools such as failure mode and effects analysis and fault tree analysis for example.

This technique helps to identify the top portion of causes that need to be addressed to resolve the majority of problems. Once the predominant causes are identified, then tools like the Ishikawa diagram or Fish-bone Analysis can be used to identify the root causes of the problems. While it is common to refer to pareto as "80/20" rule, under the assumption that, in all situations, 20% of causes determine 80% of problems, this ratio is merely a convenient rule of thumb and is not, nor should it be considered, an immutable law of nature.

The application of the Pareto analysis in risk management allows management to focus on those risks that have the most impact on the project.

Steps to identify the important causes using 80/20 rule:

1. Form a frequency of occurrences as a percentage
2. Arrange the rows in decreasing order of importance of the causes (i.e., the most important cause first)
3. Add a cumulative percentage column to the table, then plot the information
4. Plot (#1) a curve with causes on x- and cumulative percentage on y-axis
5. Plot (#2) a bar graph with causes on x- and percent frequency on y-axis
6. Draw a horizontal dotted line at 80% from the y-axis to intersect the curve. Then draw a vertical dotted line from the point of intersection to the x-axis. The vertical dotted line separates the important causes (on the left) and trivial causes (on the right)
7. Explicitly review the chart to ensure that causes for at least 80% of the problems are captured

Applications

Economics

Pareto's observation was in connection with population and wealth. Pareto noticed that approximately 80% of Italy's land was owned by 20% of the population. He then carried out surveys on a variety of other countries and found to his surprise that a similar distribution applied.

A chart that demonstrated the effect appeared in the 1992 United Nations Development Program Report, which showed that the richest 20% of the world's population receives 82.7% of the world's income. However, among nations, the Gini index shows that wealth distributions vary substantially around this norm.

Distribution of world GDP, 1989

Quintile of population	Income
Richest 20%	82.70%
Second 20%	11.75%
Third 20%	2.30%
Fourth 20%	1.85%
Poorest 20%	1.40%

The principle also holds within the tails of the distribution. The physicist Victor Yakovenko of the University of Maryland, College Park and AC Silva analyzed income data from the US Internal Revenue Service from 1983 to 2001 and found that the income distribution of the richest 1–3% of the population also follows Pareto's principle.

In Talent: How to Identify Entrepreneurs, economist Tyler Cowen and entrepreneur Daniel Gross suggest that the Pareto Principle can be applied to the role of the 20% most talented individuals in generating the majority of economic growth. According to the New York Times in 1988, many video rental shops reported that 80% of revenue came from 20% of videotapes (although rarely rented classics such as Gone with the Wind must be stocked to appear to have a good selection).

Computing

In computer science the Pareto principle can be applied to optimization efforts. For example, Microsoft noted that by fixing the top 20% of the most-reported bugs, 80% of the related errors and crashes in a given system would be eliminated. Lowell Arthur expressed that "20% of the code has 80% of the errors. Find them, fix them!" It was also discovered that, in general, 80% of a piece of software can be written in 20% of the total allocated time. Conversely, the hardest 20% of the code takes 80% of the time. This factor is usually a part of COCOMO estimating for software coding.

Occupational health and safety

Occupational health and safety professionals use the Pareto principle to underline the importance of hazard prioritization. Assuming 20% of the hazards account for 80% of the injuries, and by categorizing hazards, safety professionals can target those 20% of the hazards that cause 80% of the injuries or accidents. Alternatively, if hazards are addressed in random order, a safety professional is more likely to fix one of the 80% of hazards that account only for some fraction of the remaining 20% of injuries.

Aside from ensuring efficient accident prevention practices, the Pareto principle also ensures hazards are addressed in an economical order, because the technique ensures the utilized resources are best used to prevent the most accidents.

Engineering and quality control

The Pareto principle is the basis for the Pareto chart, one of the key tools used in total quality control and Six Sigma techniques. The Pareto principle serves as a baseline for ABC-analysis and XYZ-analysis, widely used in logistics and procurement for the purpose of optimizing stock of goods, as well as costs of keeping and replenishing that stock. In engineering control theory, such as for electromechanical energy converters, the 80/20 principle applies to optimization efforts.

The remarkable success of statistically based searches for root causes is based upon a combination of an empirical principle and mathematical logic. The empirical principle is usually known as the Pareto principle. With regard to variation causality, this principle states that there is a non-random distribution of the slopes of the numerous (theoretically infinite) terms in the general equation.

All of the terms are independent of each other by definition. Interdependent factors appear as multiplication terms. The Pareto principle states that the effect of the dominant term is very much greater than the second-largest effect term, which in turn is very much greater than the third, and so on. There is no explanation for this phenomenon; that is why we refer to it as an empirical principle.

The mathematical logic is known as the square-root-of-the-sum-of-the-squares axiom. This states that the variation caused by the steepest slope must be squared, and then the result added to the square of the variation caused by the second-steepest slope, and so on. The total observed variation is then the square root of the total sum of the variation caused by individual slopes squared. This derives from the probability density function for multiple variables or the multivariate distribution (we are treating each term as an independent variable).

The combination of the Pareto principle and the square-root-of-the-sum-of-the-squares axiom means that the strongest term in the general equation totally dominates the observed variation of effect. Thus, the strongest term will dominate the data collected for hypothesis testing.

In the systems science discipline, Joshua M. Epstein and Robert Axtell created an agent-based simulation model called Sugarscape, from a decentralized modeling approach, based on individual behavior rules defined for each agent in the economy. Wealth distribution and Pareto's 80/20 principle emerged in their results, which suggests the principle is a collective consequence of these individual rules.

Health and social outcomes

In 2009, the Agency for Healthcare Research and Quality said 20% of patients incurred 80% of healthcare expenses due to chronic conditions. A 2021 analysis showed unequal distribution of healthcare costs, with older patients and those with poorer health incurring more costs. The 80/20 rule has been proposed as a rule of thumb for the infection distribution in superspreading events. However, the degree of infectiousness has been found to be distributed continuously in the population. In epidemics with super-spreading, the majority of individuals infect relatively few secondary contacts.

See also

• 1% rule – Hypothesis that more people will lurk in a virtual community than will participate
• 10/90 gap – Health statistic
• Ninety–ninety rule – Humorous aphorism in computer programming
• Sturgeon's law – "Ninety percent of everything is crap"

Further reading

• Bookstein, Abraham (1990), "Informetric distributions, part I: Unified overview", Journal of the American Society for Information Science, 41 (5): 368–375, doi:10.1002/(SICI)1097-4571(199007)41:5<368::AID-ASI8>3.0.CO;2-C
• Klass, O. S.; Biham, O.; Levy, M.; Malcai, O.; Soloman, S. (2006), "The Forbes 400 and the Pareto wealth distribution", Economics Letters, 90 (2): 290–295, doi:10.1016/j.econlet.2005.08.020
• Koch, R. (2004), Living the 80/20 Way: Work Less, Worry Less, Succeed More, Enjoy More, London: Nicholas Brealey Publishing, ISBN 1-85788-331-4
• Reed, W. J. (2001), "The Pareto, Zipf and other power laws", Economics Letters, 74 (1): 15–19, doi:10.1016/S0165-1765(01)00524-9
• Rosen, K. T.; Resnick, M. (1980), "The size distribution of cities: an examination of the Pareto law and primacy", Journal of Urban Economics, 8 (2): 165–186, doi:10.1016/0094-1190(80)90043-1
• Rushton, A.; Oxley, J.; Croucher, P. (2000), The handbook of logistics and distribution management (2nd ed.), London: Kogan Page, ISBN 978-0-7494-3365-9.

External links

• Pareto Principle: Rule of causes and consequences
• ParetoRule.cf : Pareto Rule
• ParetoRule.cf : The Pareto Rule
• About.com: Pareto's Principle
• Wealth Condensation in Pareto Macro-Economies
• Simply Psychology: Pareto Principle (The 80-20 Rule): Examples & More