Measurement

Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.[1][2] In other words, measurement is a process of determining how large or small a physical quantity is as compared to a basic reference quantity of the same kind.[3] The scope and application of measurement are dependent on the context and discipline. In natural sciences and engineering, measurements do not apply to nominal properties of objects or events, which is consistent with the guidelines of the International vocabulary of metrology published by the International Bureau of Weights and Measures.[2] However, in other fields such as statistics as well as the social and behavioural sciences, measurements can have multiple levels, which would include nominal, ordinal, interval and ratio scales.[1][4]
Measurement is a cornerstone of trade, science, technology and quantitative research in many disciplines. Historically, many measurement systems existed for the varied fields of human existence to facilitate comparisons in these fields. Often these were achieved by local agreements between trading partners or collaborators. Since the 18th century, developments progressed towards unifying, widely accepted standards that resulted in the modern International System of Units (SI). This system reduces all physical measurements to a mathematical combination of seven base units. The science of measurement is pursued in the field of metrology.
Measurement is defined as the process of comparison of an unknown quantity with a known or standard quantity.
History
[edit]
Methodology
[edit]The measurement of a property may be categorized by the following criteria: type, magnitude, unit, and uncertainty.[citation needed] They enable unambiguous comparisons between measurements.
- The level of measurement is a taxonomy for the methodological character of a comparison. For example, two states of a property may be compared by ratio, difference, or ordinal preference. The type is commonly not explicitly expressed, but implicit in the definition of a measurement procedure.
- The magnitude is the numerical value of the characterization, usually obtained with a suitably chosen measuring instrument.
- A unit assigns a mathematical weighting factor to the magnitude that is derived as a ratio to the property of an artifact used as standard or a natural physical quantity.
- An uncertainty represents the random and systemic errors of the measurement procedure; it indicates a confidence level in the measurement. Errors are evaluated by methodically repeating measurements and considering the accuracy and precision of the measuring instrument.
Standardization of measurement units
[edit]Measurements most commonly use the International System of Units (SI) as a comparison framework. The system defines seven fundamental units: kilogram, metre, candela, second, ampere, kelvin, and mole. All of these units are defined without reference to a particular physical object which serves as a standard. Artifact-free definitions fix measurements at an exact value related to a physical constant or other invariable phenomena in nature, in contrast to standard artifacts which are subject to deterioration or destruction. Instead, the measurement unit can only ever change through increased accuracy in determining the value of the constant it is tied to.
The first proposal to tie an SI base unit to an experimental standard independent of fiat was by Charles Sanders Peirce (1839–1914),[6] who proposed to define the metre in terms of the wavelength of a spectral line.[7] This directly influenced the Michelson–Morley experiment; Michelson and Morley cite Peirce, and improve on his method.[8]
Standards
[edit]With the exception of a few fundamental quantum constants, units of measurement are derived from historical agreements. Nothing inherent in nature dictates that an inch has to be a certain length, nor that a mile is a better measure of distance than a kilometre. Over the course of human history, however, first for convenience and then for necessity, standards of measurement evolved so that communities would have certain common benchmarks. Laws regulating measurement were originally developed to prevent fraud in commerce.
Units of measurement are generally defined on a scientific basis, overseen by governmental or independent agencies, and established in international treaties, pre-eminent of which is the General Conference on Weights and Measures (CGPM), established in 1875 by the Metre Convention, overseeing the International System of Units (SI). For example, the metre was redefined in 1983 by the CGPM in terms of the speed of light, the kilogram was redefined in 2019 in terms of the Planck constant and the international yard was defined in 1960 by the governments of the United States, United Kingdom, Australia and South Africa as being exactly 0.9144 metres.
In the United States, the National Institute of Standards and Technology (NIST), a division of the United States Department of Commerce, regulates commercial measurements. In the United Kingdom, the role is performed by the National Physical Laboratory (NPL), in Australia by the National Measurement Institute,[9] in South Africa by the Council for Scientific and Industrial Research and in India the National Physical Laboratory of India.
Units and systems
[edit]unit is known or standard quantity in terms of which other physical quantities are measured.

Imperial and US customary systems
[edit]Before SI units were widely adopted around the world, the British systems of English units and later imperial units were used in Britain, the Commonwealth and the United States. The system came to be known as U.S. customary units in the United States and is still in use there and in a few Caribbean countries. These various systems of measurement have at times been called foot-pound-second systems after the Imperial units for length, weight and time even though the tons, hundredweights, gallons, and nautical miles, for example, are different for the U.S. units. Many Imperial units remain in use in Britain, which has officially switched to the SI system—with a few exceptions such as road signs, which are still in miles. Draught beer and cider must be sold by the imperial pint, and milk in returnable bottles can be sold by the imperial pint. Many people measure their height in feet and inches and their weight in stone and pounds, to give just a few examples. Imperial units are used in many other places, for example, in many Commonwealth countries that are considered metricated, land area is measured in acres and floor space in square feet, particularly for commercial transactions (rather than government statistics). Similarly, gasoline is sold by the gallon in many countries that are considered metricated.
Metric system
[edit]The metric system is a decimal system of measurement based on its units for length, the metre and for mass, the kilogram. It exists in several variations, with different choices of base units, though these do not affect its day-to-day use. Since the 1960s, the International System of Units (SI) is the internationally recognised metric system. Metric units of mass, length, and electricity are widely used around the world for both everyday and scientific purposes.
International System of Units
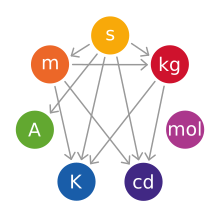
[edit]The International System of Units (abbreviated as SI from the French language name Système International d'Unités) is the modern revision of the metric system. It is the world's most widely used system of units, both in everyday commerce and in science. The SI was developed in 1960 from the metre–kilogram–second (MKS) system, rather than the centimetre–gram–second (CGS) system, which, in turn, had many variants. The SI units for the seven base physical quantities are:[10]
| Base quantity | Base unit | Symbol | Defining constant |
|---|---|---|---|
| time | second | s | hyperfine splitting in caesium-133 |
| length | metre | m | speed of light, c |
| mass | kilogram | kg | Planck constant, h |
| electric current | ampere | A | elementary charge, e |
| temperature | kelvin | K | Boltzmann constant, k |
| amount of substance | mol | mol | Avogadro constant, NA |
| luminous intensity | candela | cd | luminous efficacy of a 540 THz source, Kcd |
In the SI, base units are the simple measurements for time, length, mass, temperature, amount of substance, electric current and light intensity. Derived units are constructed from the base units, for example, the watt, i.e. the unit for power, is defined from the base units as m2·kg·s−3. Other physical properties may be measured in compound units, such as material density, measured in kg/m3.
Converting prefixes
[edit]The SI allows easy multiplication when switching among units having the same base but different prefixes. To convert from metres to centimetres it is only necessary to multiply the number of metres by 100, since there are 100 centimetres in a metre. Inversely, to switch from centimetres to metres one multiplies the number of centimetres by 0.01 or divides the number of centimetres by 100.
Length
[edit]
A ruler or rule is a tool used in, for example, geometry, technical drawing, engineering, and carpentry, to measure lengths or distances or to draw straight lines. Strictly speaking, the ruler is the instrument used to rule straight lines and the calibrated instrument used for determining length is called a measure, however common usage calls both instruments rulers and the special name straightedge is used for an unmarked rule. The use of the word measure, in the sense of a measuring instrument, only survives in the phrase tape measure, an instrument that can be used to measure but cannot be used to draw straight lines. As can be seen in the photographs on this page, a two-metre carpenter's rule can be folded down to a length of only 20 centimetres, to easily fit in a pocket, and a five-metre-long tape measure easily retracts to fit within a small housing.
Time
[edit]Time is an abstract measurement of elemental changes over a non-spatial continuum. It is denoted by numbers and/or named periods such as hours, days, weeks, months and years. It is an apparently irreversible series of occurrences within this non spatial continuum. It is also used to denote an interval between two relative points on this continuum.
Mass
[edit]Mass refers to the intrinsic property of all material objects to resist changes in their momentum. Weight, on the other hand, refers to the downward force produced when a mass is in a gravitational field. In free fall, (no net gravitational forces) objects lack weight but retain their mass. The Imperial units of mass include the ounce, pound, and ton. The metric units gram and kilogram are units of mass.
One device for measuring weight or mass is called a weighing scale or, often, simply a scale. A spring scale measures force but not mass, a balance compares weight, both require a gravitational field to operate. Some of the most accurate instruments for measuring weight or mass are based on load cells with a digital read-out, but require a gravitational field to function and would not work in free fall.
Economics
[edit]The measures used in economics are physical measures, nominal price value measures and real price measures. These measures differ from one another by the variables they measure and by the variables excluded from measurements.
Survey research
[edit]
In the field of survey research, measures are taken from individual attitudes, values, and behavior using questionnaires as a measurement instrument. As all other measurements, measurement in survey research is also vulnerable to measurement error, i.e. the departure from the true value of the measurement and the value provided using the measurement instrument.[11] In substantive survey research, measurement error can lead to biased conclusions and wrongly estimated effects. In order to get accurate results, when measurement errors appear, the results need to be corrected for measurement errors.
Exactness designation
[edit]The following rules generally apply for displaying the exactness of measurements:[12]
- All non-0 digits and any 0s appearing between them are significant for the exactness of any number. For example, the number 12000 has two significant digits, and has implied limits of 11500 and 12500.
- Additional 0s may be added after a decimal separator to denote a greater exactness, increasing the number of decimals. For example, 1 has implied limits of 0.5 and 1.5 whereas 1.0 has implied limits 0.95 and 1.05.
Difficulties
[edit]Since accurate measurement is essential in many fields, and since all measurements are necessarily approximations, a great deal of effort must be taken to make measurements as accurate as possible. For example, consider the problem of measuring the time it takes an object to fall a distance of one metre (about 39 in). Using physics, it can be shown that, in the gravitational field of the Earth, it should take any object about 0.45 second to fall one metre. However, the following are just some of the sources of error that arise:
- This computation used for the acceleration of gravity 9.8 metres per second squared (32 ft/s2). But this measurement is not exact, but only precise to two significant digits.
- The Earth's gravitational field varies slightly depending on height above sea level and other factors.
- The computation of 0.45 seconds involved extracting a square root, a mathematical operation that required rounding off to some number of significant digits, in this case two significant digits.
Additionally, other sources of experimental error include:
- carelessness,
- determining of the exact time at which the object is released and the exact time it hits the ground,
- measurement of the height and the measurement of the time both involve some error,
- air resistance,
- posture of human participants.[13]
Scientific experiments must be carried out with great care to eliminate as much error as possible, and to keep error estimates realistic.
Definitions and theories
[edit]Classical definition
[edit]In the classical definition, which is standard throughout the physical sciences, measurement is the determination or estimation of ratios of quantities.[14] Quantity and measurement are mutually defined: quantitative attributes are those possible to measure, at least in principle. The classical concept of quantity can be traced back to John Wallis and Isaac Newton, and was foreshadowed in Euclid's Elements.[14]
Representational theory
[edit]In the representational theory, measurement is defined as "the correlation of numbers with entities that are not numbers".[15] The most technically elaborated form of representational theory is also known as additive conjoint measurement. In this form of representational theory, numbers are assigned based on correspondences or similarities between the structure of number systems and the structure of qualitative systems. A property is quantitative if such structural similarities can be established. In weaker forms of representational theory, such as that implicit within the work of Stanley Smith Stevens,[16] numbers need only be assigned according to a rule.
The concept of measurement is often misunderstood as merely the assignment of a value, but it is possible to assign a value in a way that is not a measurement in terms of the requirements of additive conjoint measurement. One may assign a value to a person's height, but unless it can be established that there is a correlation between measurements of height and empirical relations, it is not a measurement according to additive conjoint measurement theory. Likewise, computing and assigning arbitrary values, like the "book value" of an asset in accounting, is not a measurement because it does not satisfy the necessary criteria.
Three type of representational theory
-
- Empirical relation
- In science, an empirical relationship is a relationship or correlation based solely on observation rather than theory. An empirical relationship requires only confirmatory data irrespective of theoretical basis.
-
- The rule of mapping
- The real world is the Domain of mapping, and the mathematical world is the range. when we map the attribute to mathematical system, we have many choice for mapping and the range.
-
- The representation condition of measurement
Theory
[edit]All data are inexact and statistical in nature. Thus the definition of measurement is: "A set of observations that reduce uncertainty where the result is expressed as a quantity."[17] This definition is implied in what scientists actually do when they measure something and report both the mean and statistics of the measurements. In practical terms, one begins with an initial guess as to the expected value of a quantity, and then, using various methods and instruments, reduces the uncertainty in the value. In this view, unlike the positivist representational theory, all measurements are uncertain, so instead of assigning one value, a range of values is assigned to a measurement. This also implies that there is not a clear or neat distinction between estimation and measurement.
Quantum mechanics
[edit]In quantum mechanics, a measurement is an action that determines a particular property (such as position, momentum, or energy) of a quantum system. Quantum measurements are always statistical samples from a probability distribution; the distribution for many quantum phenomena is discrete, not continuous.[18]: 197 Quantum measurements alter quantum states and yet repeated measurements on a quantum state are reproducible. The measurement appears to act as a filter, changing the quantum state into one with the single measured quantum value.[18] The unambiguous meaning of the quantum measurement is an unresolved fundamental problem in quantum mechanics; the most common interpretation is that when a measurement is performed, the wavefunction of the quantum system "collapses" to a single, definite value.[19]
Biology
[edit]In biology, there is generally no well established theory of measurement. However, the importance of the theoretical context is emphasized.[20] Moreover, the theoretical context stemming from the theory of evolution leads to articulate the theory of measurement and historicity as a fundamental notion.[21] Among the most developed fields of measurement in biology are the measurement of genetic diversity and species diversity.[22]
See also
[edit]- Conversion of units
- Electrical measurements
- History of measurement
- ISO 10012, Measurement management systems
- Levels of measurement
- List of humorous units of measurement
- List of unusual units of measurement
- Measurement in quantum mechanics
- Measurement uncertainty
- NCSL International
- Observable quantity
- Orders of magnitude
- Quantification (science)
- Standard (metrology)
- Timeline of temperature and pressure measurement technology
- Timeline of time measurement technology
- Weights and measures
References
[edit]- ^ a b Pedhazur, Elazar J.; Schmelkin, Leora and Albert (1991). Measurement, Design, and Analysis: An Integrated Approach (1st ed.). Hillsdale, NJ: Lawrence Erlbaum Associates. pp. 15–29. ISBN 978-0-8058-1063-9.
- ^ a b International Vocabulary of Metrology – Basic and General Concepts and Associated Terms (VIM) (PDF) (3rd ed.). International Bureau of Weights and Measures. 2008. p. 16.
- ^ Young, Hugh D; Freedman, Roger A. (2012). University Physics (13 ed.). Pearson Education Inc. ISBN 978-0-321-69686-1.
- ^ Kirch, Wilhelm, ed. (2008). "Level of measurement". Encyclopedia of Public Health. Vol. 2. Springer. p. 81. ISBN 978-0-321-02106-9.
- ^ "A Brief History of Metrology - bowersUK". bowers rest of world. Retrieved 2024-10-10.
- ^ Crease 2011, pp. 182–4
- ^ C.S. Peirce (July 1879) "Note on the Progress of Experiments for Comparing a Wave-length with a Metre" American Journal of Science, as referenced by Crease 2011, p. 203
- ^ Crease, Robert P. (2011). World in the Balance: The Historical Quest for an Absolute System of Measurement. New York & London: W. W. Norton. p. 203. ISBN 978-0-393-34354-0.
- ^ "About Us". National Measurement Institute of Australia. 3 December 2020.
- ^ The International System of Units (PDF) (9th ed.), International Bureau of Weights and Measures, Dec 2022, ISBN 978-92-822-2272-0
- ^ Groves, Robert (2004). Survey Methodology. New Jersey: Wiley. ISBN 9780471483489. "By measurement error we mean a departure from the value of the measurement as applied to a sample unit and the value provided. " pp. 51–52 .
- ^ Page 41 in: VanPool, Todd (2011). Quantitative analysis in archaeology. Chichester Malden: Wiley-Blackwell. ISBN 978-1-4443-9017-9. OCLC 811317577.
- ^ Gill, Simeon; Parker, Christopher J. (2017). "Scan posture definition and hip girth measurement: the impact on clothing design and body scanning". Ergonomics. 60 (8): 1123–1136. doi:10.1080/00140139.2016.1251621. PMID 27764997. S2CID 23758581.
- ^ a b Michell, J. (1999). Measurement in psychology: a critical history of a methodological concept. New York: Cambridge University Press.
- ^ Ernest Nagel: "Measurement", Erkenntnis, Volume 2, Number 1 / December 1931, pp. 313–335, published by Springer, the Netherlands
- ^ Stevens, S.S. On the theory of scales and measurement 1946. Science. 103, 677–80.
- ^ Douglas Hubbard: "How to Measure Anything", Wiley (2007), p. 21
- ^ a b Messiah, Albert (1966). Quantum Mechanics. North Holland, John Wiley & Sons. ISBN 0486409244.
- ^ Penrose, Roger (2007). The road to reality : a complete guide to the laws of the universe. New York: Vintage Books. ISBN 978-0-679-77631-4. "The jumping of the quantum state to one of the eigenstates of Q is the process referred to as state-vector reduction or collapse of the wavefunction. It is one of quantum theory's most puzzling features ..." "[T]he way in which quantum mechanics is used in practice is to take the state indeed to jump in this curious way whenever a measurement is deemed to take place." p 528 Later Chapter 29 is entitled the Measurement paradox.
- ^ Houle, David; Pélabon, Christophe; Wagner, Günter P.; Hansen, Thomas F. (2011). "Measurement and Meaning in Biology" (PDF). The Quarterly Review of Biology. 86 (1): 3–34. doi:10.1086/658408. ISSN 0033-5770. PMID 21495498. S2CID 570080. Archived from the original (PDF) on 2019-05-29.
- ^ Montévil, Maël (2019). "Measurement in biology is methodized by theory". Biology & Philosophy. 34 (3). doi:10.1007/s10539-019-9687-x. ISSN 0169-3867. S2CID 96447209.
- ^ Magurran, A.E. & McGill, B.J. (Hg.) 2011: Biological Diversity: Frontiers in Measurement and Assessment Oxford University Press.
External links
[edit] Media related to Measurement at Wikimedia Commons
Media related to Measurement at Wikimedia Commons- Schlaudt, Oliver 2020: "measurement". In: Kirchhoff, Thomas (ed.): Online Encyclopedia Philosophy of Nature. Heidelberg: Universitätsbibliothek Heidelberg, measurement.
- Tal, Era 2020: "Measurement in Science". In: Zalta, Edward N. (ed.): The Stanford Encyclopedia of Philosophy (Fall 2020 ed.), Measurement in Science.
- Ball, Robert Stawell (1883). . Encyclopædia Britannica. Vol. XV (9th ed.). pp. 659–668.
- A Dictionary of Units of Measurement Archived 2018-10-06 at the Wayback Machine
- 'Metrology – in short' 3rd ed., July 2008 ISBN 978-87-988154-5-7
