Multiplication (music)

The mathematical operations of multiplication have several applications to music. Other than its application to the frequency ratios of intervals (for example, Just intonation, and the twelfth root of two in equal temperament), it has been used in other ways for twelve-tone technique, and musical set theory. Additionally ring modulation is an electrical audio process involving multiplication that has been used for musical effect.

A multiplicative operation is a mapping in which the argument is multiplied.^[3] Multiplication originated intuitively in interval expansion, including tone row order number rotation, for example in the music of Béla Bartók and Alban Berg.^[4] Pitch number rotation, Fünferreihe or "five-series" and Siebenerreihe or "seven-series", was first described by Ernst Krenek in Über neue Musik.^[5]^[4] Princeton-based theorists, including James K. Randall,^[6] Godfrey Winham,^[7] and Hubert S. Howe^[8] "were the first to discuss and adopt them, not only with regards [sic] to twelve-tone series".^[9]

Pitch-class multiplication modulo 12

When dealing with pitch-class sets, multiplication modulo 12 is a common operation. Dealing with all twelve tones, or a tone row, there are only a few numbers which one may multiply a row by and still end up with a set of twelve distinct tones. Taking the prime or unaltered form as P₀, multiplication is indicated by M_x, x being the multiplicator:

M_x(y) ≡ xy mod 12

The following table lists all possible multiplications of a chromatic twelve-tone row:

M
0	0	0	0	0	0	0	0	0	0	0	0
1	1	2	3	4	5	6	7	8	9	10	11
2	2	4	6	8	10	0	2	4	6	8	10
3	3	6	9	0	3	6	9	0	3	6	9
4	4	8	0	4	8	0	4	8	0	4	8
5	5	10	3	8	1	6	11	4	9	2	7
6	6	0	6	0	6	0	6	0	6	0	6
7	7	2	9	4	11	6	1	8	3	10	5
8	8	4	0	8	4	0	8	4	0	8	4
9	9	6	3	0	9	6	3	0	9	6	3
10	10	8	6	4	2	0	10	8	6	4	2
11	11	10	9	8	7	6	5	4	3	2	1

Note that only M₁, M₅, M₇, and M₁₁ give a one-to-one mapping (a complete set of 12 unique tones). This is because each of these numbers is relatively prime to 12. Also interesting is that the chromatic scale is mapped to the circle of fourths with M₅, or fifths with M₇, and more generally under M₇ all even numbers stay the same while odd numbers are transposed by a tritone. This kind of multiplication is frequently combined with a transposition operation. It was first described in print by Herbert Eimert, under the terms "Quartverwandlung" (fourth transformation) and "Quintverwandlung" (fifth transformation),^[10] and has been used by the composers Milton Babbitt,^[11]^[12] Robert Morris,^[13] and Charles Wuorinen.^[14] This operation also accounts for certain harmonic transformations in jazz.^[15]

Thus multiplication by the two meaningful operations (5 & 7) may be designated with M₅(a) and M₇(a) or M and IM.^[4]

M₁ = Identity
M₅ = Cycle of fourths transform
M₇ = Cycle of fifths transform
M₁₁ = Inversion
M₁₁M₅ = M₇
M₇M₅ = M₁₁
M₅M₅ = M₁
M₇M₁₁M₅ = M₁
...

Pitch multiplication

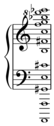
Pierre Boulez^[16]^{[dubious – discuss]} described an operation he called pitch multiplication, which is somewhat akin ^{[clarification needed]} to the Cartesian product of pitch-class sets. Given two sets, the result of pitch multiplication will be the set of sums (modulo 12) of all possible pairings of elements between the original two sets. Its definition:

X\times Y=\{(x+y){\bmod {1}}2|x\in X,y\in Y\}

For example, if multiplying a C-major chord $\{0,4,7\}$ with a dyad containing C,D $\{0,2\}$ , the result is:

\{0,4,7\}\times \{0,2\}=\{0,2,4,6,7,9\}

In this example, a set of three pitches multiplied with a set of two pitches gives a new set of 3 × 2 pitches. Given the limited space of modulo 12 arithmetic, when using this procedure very often duplicate tones are produced, which are generally omitted. This technique was used most famously in Boulez's 1955 Le Marteau sans maître, as well as in his Third Piano Sonata, Structures II, "Don" and "Tombeau" from Pli selon pli, Éclat (and Éclat/Multiples), Figures—Doubles—Prismes, Domaines, and Cummings ist der Dichter, as well as the withdrawn choral work, Oubli signal lapidé (1952).^[17]^[18]^[19] This operation, like arithmetic multiplication and transpositional combination of set classes, is commutative.^[20]

Howard Hanson called this operation of commutative mathematical convolution "superposition"^[21] or "@-projection" and used the "/" notation interchangeably. Thus "p@m" or "p/m" means "perfect fifth at major third", e.g.: { C E G B }. He specifically noted that two triad forms could be so multiplied, or a triad multiplied by itself, to produce a resultant scale. The latter "squaring" of a triad produces a particular scale highly saturated in instances of the source triad.^[22] Thus "pmn", Hanson's name for common the major triad, when squared, is "PMN", e.g.: { C D E G G♯ B }.

Nicolas Slonimsky used this operation, non-generalized, to form 1300 scales by multiplying the symmetric tritones, augmented chords, diminished seventh chords, and wholetone scales by the sum of 3 factors which he called interpolation, infrapolation, and ultrapolation.^[23] The combination of interpolation, infrapolation, and ultrapolation, forming obliquely infra-interpolation, infra-ultrapolation, and infra-inter-ultrapolation, additively sums to what is effectively a second sonority. This second sonority, multiplied by the first, gives his formula for generating scales and their harmonizations.

Joseph Schillinger used the idea, undeveloped, to categorize common 19th- and early 20th-century harmonic styles as product of horizontal harmonic root-motion and vertical harmonic structure.^[24] Some of the composers' styles which he cites appear in the following multiplication table.

	Chord type
Root Scale	Major chord	Augmented chord	Minor chord	Diminished seventh chord
Diminished seventh chord	Octatonic scale Richard Wagner	Chromatic scale	Octatonic scale
Augmented chord	Augmented scale Franz Liszt	Claude Debussy Maurice Ravel	Augmented scale Nikolai Rimsky-Korsakov
Whole tone scale	Chromatic scale Claude Debussy Maurice Ravel	Whole tone scale Claude Debussy Maurice Ravel	Chromatic scale Claude Debussy Maurice Ravel
Chromatic scale	Chromatic scale Richard Wagner	Chromatic scale	Chromatic scale	Chromatic scale
Quartal chord	Major scale		Natural minor scale
Major chord	6-note analog of harmonic major scale	Augmented scale		Octatonic scale
Minor chord		Augmented scale	6-note analog of harmonic major scale	Octatonic scale
Diatonic scale	Undecatonic scale	Chromatic scale	Undecatonic scale	Chromatic scale

The approximation of the 12 pitches of Western music by modulus-12 math, forming the Circle of Halfsteps, means that musical intervals can also be thought of as angles in a polar coordinate system, stacking of identical intervals as functions of harmonic motion, and transposition as rotation around an axis. Thus, in the multiplication example above from Hanson, "p@m" or "p/m" ("perfect 5th at major 3rd", e.g.: { C E G B }) also means "perfect fifth, superimposed upon perfect fifth rotated 1/3 of the circumference of the Circle of Halfsteps". A conversion table of intervals to angular measure (taken as negative numbers for clockwise rotation) follows:

Interval	Circle of halfsteps			Circle of fifths
Interval	Halfsteps	Radians	Degrees	Fifths	Radians	Degrees
Unison	0	0	0	0	0	0
Minor second	1	⁠ $π$ /6⁠	30	7	⁠7 $π$ /6⁠	210
Major second	2	⁠ $π$ /3⁠	60	2	⁠ $π$ /3⁠	60
Minor third	3	⁠ $π$ /2⁠	90	9	⁠3 $π$ /2⁠	270
Major third	4	⁠2 $π$ /3⁠	120	4	⁠2 $π$ /3⁠	120
Perfect fourth	5	⁠5 $π$ /6⁠	150	11	⁠11 $π$ /6⁠	330
Diminished fifth or Augmented fourth	6	$π$	180	6	$π$	180
Perfect fifth	7	⁠7 $π$ /6⁠	210	1	⁠ $π$ /6⁠	30
Minor sixth	8	⁠4 $π$ /3⁠	240	8	⁠4 $π$ /3⁠	240
Major sixth	9	⁠3 $π$ /2⁠	270	3	⁠ $π$ /2⁠	90
Minor seventh	10	⁠5 $π$ /3⁠	300	10	⁠5 $π$ /3⁠	300
Major seventh	11	⁠11 $π$ /6⁠	330	5	⁠5 $π$ /6⁠	150
Octave	12	2 $π$	360	12	2 $π$	360

This angular interpretation of intervals is helpful to visualize a very practical example of multiplication in music: Euler-Fokker genera used in describing the Just intonation tuning of keyboard instruments.^[25] Each genus represents an harmonic function such as "3 perfect fifths stacked" or other sonority such as { C G D F♯ }, which, when multiplied by the correct angle(s) of copy, approximately fills the 12TET circumferential space of the Circle of fifths. It would be possible, though not musically pretty, to tune an augmented triad of two perfect non-beating major thirds, then (multiplying) tune two tempered fifths above and 1 below each note of the augmented chord; this is Euler-Fokker genus [555]. A different result is obtained by starting with the "3 perfect fifths stacked", and from these non-beating notes tuning a tempered major third above and below; this is Euler-Fokker genus [333].

Time multiplication

Joseph Schillinger described an operation of "polynomial time multiplication" (polynomial refers to any rhythm consisting of more than one duration) corresponding roughly to that of Pitch multiplication above.^[26] A theme, reduced to a consistent series of integers representing the quarter, 8th-, or 16th-note duration of each of the notes of the theme, could be multiplied by itself or the series of another theme to produce a coherent and related variation. Especially, a theme's series could be squared or cubed or taken to higher powers to produce a saturation of related material.

Affine transformation

Herbert Eimert described what he called the "eight modes" of the twelve-tone series, all mirror forms of one another. The inverse is obtained through a horizontal mirror, the retrograde through a vertical mirror, the retrograde-inverse through both a horizontal and a vertical mirror, and the "cycle-of-fourths-transform" or Quartverwandlung and "cycle-of-fifths-transform" or Quintverwandlung obtained through a slanting mirror.^[28] With the retrogrades of these transforms and the prime, there are eight permutations.

Furthermore, one can sort of move the mirror at an angle, that is the 'angle' of a fourth or fifth, so that the chromatic row is reflected in both cycles. ... In this way, one obtains the cycle-of-fourths transform and the cycle-of-fifths transform of the row.<ref>Eimert 1950, 29, translated in Schuijer 2008, 81

Joseph Schillinger embraced not only contrapuntal inverse, retrograde, and retrograde-inverse—operations of matrix multiplication in Euclidean vector space—but also their rhythmic counterparts as well. Thus he could describe a variation of theme using the same pitches in same order, but employing its original time values in retrograde order. He saw the scope of this multiplicatory universe beyond simple reflection, to include transposition and rotation (possibly with projection back to source), as well as dilation which had formerly been limited in use to the time dimension (via augmentation and diminution).^[29] Thus he could describe another variation of theme, or even of a basic scale, by multiplying the halfstep counts between each successive pair of notes by some factor, possibly normalizing to the octave via Modulo-12 operation,(^[30]

Z-relation

Some Z-related chords are connected by M or IM (multiplication by 5 or multiplication by 7), due to identical entries for 1 and 5 on the APIC vector.^[31]

References

^ Antokoletz 1993, 260, cited in Schuijer 2008, 77–78
^ Schuijer 2008, 79.
^ Rahn 1980, 53.
^ ^a ^b ^c Schuijer 2008, 77–78.
^ Krenek 1937.
^ Randall 1962.
^ Winham 1970.
^ Howe 1965.
^ Schuijer 2008, 81.
^ Eimert 1950, 29–33.
^ Morris 1997, 238 & 242–43.
^ Winham 1970, 65–66.
^ Morris 1997, 238–239, 243.
^ Hibbard 1969, 157–158.
^ Morris 1982, 153–154.
^ Boulez 1971, 39-40, 79-80.
^ Koblyakov 1990, 32.
^ Heinemann 1993.
^ Heinemann 1998.
^ Heinemann 1993, 24.
^ Hanson 1960, 44, 167.
^ Hanson 1960, 167.
^ Slonimsky 1947, v.
^ Schillinger 1941, 147.
^ Fokker 1987.
^ Schillinger 1941, 70–? ^{[page needed]}.
^ Eimert 1950, ^{[page needed]} as reproduced with minor alterations in Schuijer 2008, 80
^ Eimert 1950, 28–29.
^ Schillinger 1941, 187ff ^{[page needed]}.
^ Schillinger 1941, 115ff, 208ff ^{[page needed]}.
^ Schuijer 2008, 98n18.

Sources

Antokoletz, Elliott. 1993. "Middle Period String Quartets". In The Bartok Companion, edited by Malcolm Gillies, 257–277. London: Faber and Faber. ISBN 0-571-15330-5 (cased); ISBN 0-571-15331-3 (pbk).
Boulez, Pierre. 1971. Boulez on Music Today. Translated by Susan Bradshaw and Richard Rodney Bennett. Cambridge, Massachusetts: Harvard University Press. ISBN 0-674-08006-8.
Eimert, Herbert. 1950. Lehrbuch der Zwölftontechnik. Wiesbaden: Breitkopf & Härtel.
Fokker, Adriaan Daniël. 1987. Selected Musical Compositions. Utrecht: The Diapason Press. ISBN 90-70907-11-9.
Hanson, Howard. 1960. Harmonic Materials of Modern Music. New York: Appleton-Century-Crofts.
Heinemann, Stephen. 1993. Pitch-Class Set Multiplication in Boulez's Le Marteau sans maître. D.M.A. diss., University of Washington.
Heinemann, Stephen. 1998. "Pitch-Class Set Multiplication in Theory and Practice." Music Theory Spectrum 20, no. 1 (Spring): 72–96.
Hibbard, William. 1969. "Charles Wuorinen: The Politics of Harmony". Perspectives of New Music 7, no. 2 (Spring-Summer): 155–166.
Howe, Hubert S. 1965. "Some Combinational Properties of Pitch Structures." Perspectives of New Music 4, no. 1 (Fall-Winter): 45–61.
Koblyakov, Lev. 1990. Pierre Boulez: A World of Harmony. Chur: Harwood Academic Publishers. ISBN 3-7186-0422-1.
Krenek, Ernst. 1937. Über neue Musik: Sechs Vorlesungen zur Einführung in die theoretischen Grundlagen. Vienna: Ringbuchhandlung.
Morris, Robert D. 1982. Review: "John Rahn, Basic Atonal Theory. New York: Longman, 1980". Music Theory Spectrum 4:138–154.
Morris, Robert D. 1997. "Some Remarks on Odds and Ends". Perspectives of New Music 35, no. 2 (Summer): 237–256.
Rahn, John. 1980. Basic Atonal Theory. Longman Music Series. New York and London: Longman. Reprinted, New York: Schirmer Books; London: Collier Macmillan, 1987.
Randall, James K. 1962. "Pitch-Time Correlation". Unpublished. Cited in Schuijer 2008, 82.
Schillinger, Joseph. 1941. The Schillinger System of Musical Composition. New York: Carl Fischer. ISBN 0306775220.
Schuijer, Michiel. 2008. Analyzing Atonal Music: Pitch-Class Set Theory and Its Contexts. Eastman Studies in Music 60. Rochester, New York: University of Rochester Press. ISBN 978-1-58046-270-9.
Slonimsky, Nicolas. 1947. Thesaurus of Scales and Melodic Patterns. New York: Charles Scribner Sons. ISBN 002-6118505.
Winham, Godfrey. 1970. "Composition with Arrays". Perspectives of New Music 9, no. 1 (Fall-Winter): 43–67.

v t e Musical set theory
All-interval tetrachord All-trichord hexachord Complement Forte number Identity Interval class Interval vector Multiplication Permutation Pitch class Pitch interval Pitch-interval class Set List Similarity relation Transformation Z-relation
Diatonic set theory	Bisector Cardinality equals variety Common tone (Deep scale property) Diatonic scale Generated collection Generic and specific intervals (Myhill's property) Maximal evenness Rothenberg propriety Structure implies multiplicity

v t e Twelve-tone technique and serialism
Fundamentals	Combinatoriality Complementation Derivation Hexachord Interval class Invariance Partition Cross partition Tone row Aggregate List
Permutations	Prime row Retrograde Inversion Retrograde inversion Multiplication
Notable composers	Milton Babbitt Pierre Boulez Josef Matthias Hauer Second Viennese School Alban Berg Arnold Schoenberg Anton Webern Charles Wuorinen ...more...
Related articles	All-interval twelve-tone row All-trichord hexachord Atonality Chromatic scale Duration series Equivalence Formula composition Modernism (music) Punctualism Semitone Set theory Time point Trope
List of dodecaphonic and serial compositions