Golden rectangle

In geometry, a golden rectangle is a rectangle whose side lengths are in the golden ratio, $1:{\tfrac {1+{\sqrt {5}}}{2}}$ , which is $1:\varphi$ (the Greek letter phi), where $\varphi$ is approximately 1.618.

Golden rectangles exhibit a special form of self-similarity: All rectangles created by adding a square to a side, or removing a square from an end, of a golden rectangle are golden rectangles as well.

Construction

A golden rectangle can be constructed with only a straightedge and compass in four steps:

Draw a square
Draw a line from the midpoint of one side of the square to an opposite corner
Use that line as the radius to draw an arc that defines the height of the rectangle
Complete the golden rectangle

A distinctive feature of this shape is that when a square section is added—or removed—the product is another golden rectangle, having the same aspect ratio as the first. Square addition or removal can be repeated infinitely, in which case corresponding corners of the squares form an infinite sequence of points on the golden spiral, the unique logarithmic spiral with this property. Diagonal lines drawn between the first two orders of embedded golden rectangles will define the intersection point of the diagonals of all the embedded golden rectangles; Clifford A. Pickover referred to this point as "the Eye of God".^[2]

In practise, a simple made to measure method of construction is possible using only a ruler, a set square and a calculator.

By limiting the value of Phi to 3 decimal places (φ = 1.618) a visually accurate golden rectangle can be described based on either length or height with only 1 millimetre per metre inaccuracy:

Assume the short side of the rectangle to be "a" and its long side to be "ab".

If "a" is known, then "ab" will be the length of "a" increased by 61.8% ie: ab = a + 61.8% (via calculator) or ab = (a × 1.618) manually.
If "ab" is known, then "a" will be the length of "ab" decreased by 38.2% ie: a = ab – 38.2% (via calculator) or a = (ab × 0.618) manually.

History

The proportions of the golden rectangle have been observed as early as the Babylonian Tablet of Shamash (c. 888–855 BC),^[3]^[4] though Mario Livio calls any knowledge of the golden ratio before the Ancient Greeks "doubtful".^[5]

According to Livio, since the publication of Luca Pacioli's Divina proportione in 1509, "the Golden Ratio started to become available to artists in theoretical treatises that were not overly mathematical, that they could actually use."^[6]

The 1927 Villa Stein designed by Le Corbusier, some of whose architecture utilizes the golden ratio, features dimensions that closely approximate golden rectangles.^[7]

Relation to regular polygons and polyhedra

Construction of half-golden rectangle (central right triangle) from polygons

Three golden rectangles in an icosahedron

Euclid gives an alternative construction of the golden rectangle using three polygons circumscribed by congruent circles: a regular decagon, hexagon, and pentagon. The respective lengths a, b, and c of the sides of these three polygons satisfy the equation a² + b² = c², so line segments with these lengths form a right triangle (by the converse of the Pythagorean theorem). The ratio of the side length of the hexagon to the decagon is the golden ratio, so this triangle forms half of a golden rectangle.^[8]

The convex hull of two opposite edges of a regular icosahedron forms a golden rectangle. The twelve vertices of the icosahedron can be decomposed in this way into three mutually-perpendicular golden rectangles, whose boundaries are linked in the pattern of the Borromean rings.^[9]

Relation to angles of the golden triangle

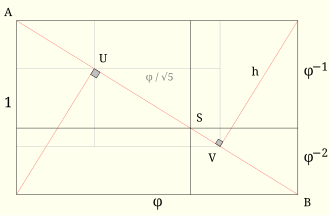
Assume a golden rectangle has been constructed as indicated above, with height $1$ , length ⁠ $\varphi$ ⁠ and diagonal length ${\sqrt {\varphi ^{2}+1}}$ . The triangles on the diagonal have altitudes $1/{\sqrt {1+\varphi ^{-2}}}\,;$ each perpendicular foot divides the diagonal in ratio ⁠ $\varphi ^{2}.$ ⁠

If an horizontal line is drawn through the intersection point of the diagonal and the internal edge of the square, the original golden rectangle and the two scaled copies along the diagonal have linear sizes in the ratios $\varphi ^{2}:\varphi :1\,,$ the square and rectangle opposite the diagonal both have areas equal to ⁠ $\varphi ^{-2}.$ ⁠^[10]

Relative to vertex $A$ , the coordinates of feet of altitudes $U$ and $V$ are $\left({\tfrac {1}{\sqrt {5}}},{\tfrac {1}{\varphi {\sqrt {5}}}}\right)$ and $\left({\tfrac {\varphi ^{2}}{\sqrt {5}}},{\tfrac {\varphi }{\sqrt {5}}}\right)$ ; the length of line segment ⁠ ${\overline {UV}}$ ⁠ is equal to altitude ⁠ $h.$ ⁠

If the diagram is further subdivided by perpendicular lines through $U$ and $V$ , the lengths of the diagonal and its subsections can be expressed as trigonometric functions of arguments 72 and 36 degrees, the angles of the golden triangle:

{\begin{aligned}{\overline {AB}}+{\overline {AS}}&=\tan(72)\\{\overline {AB}}={\sqrt {\varphi ^{2}+1}}&=2\sin(72)\\{\overline {AV}}=\varphi /{\overline {AS}}&=\cot(36)\\{\overline {AS}}={\sqrt {1+\varphi ^{-2}}}&=2\sin(36)\\{\overline {UV}}=1/{\overline {AS}}&=\cot(36)/\varphi \\{\overline {SB}}={\overline {AS}}/\varphi &=\tan(36)\\{\overline {US}}=2/(\varphi {\overline {AB}})&=2\cot(72)\\{\overline {AU}}=1/{\overline {AB}}&=\varphi \cot(72)\\{\overline {AS}}-{\overline {UV}}&=\cot(72)\\{\overline {SV}}=(2-\varphi )/{\overline {AB}}&=\cot(72)/\varphi ,\end{aligned}}

with ⁠

\varphi =2\cos(36).

⁠

Both the lengths of the diagonal sections and the trigonometric values are elements of quartic number field $K=\mathbb {Q} \left({\sqrt {(5+{\sqrt {5}})/2}}\right).$

Interpreting the line segments as musical string lengths results in a set of ten corresponding pitches, one of which doubles at the octave. Mapping the intervals in logarithmic scale — with the 'golden octave' equal to ⁠ $\varphi ^{4}$ ⁠ — reveals equally tempered 100 cents semitones. An analysis in musical terms is substantiated by the single exceptional pitch proportional to line segment ⁠ ${\overline {US}}$ ⁠, which approximates the harmonic seventh within remarkable one cent accuracy.

This set of ten tones can be partitioned into two modes of the pentatonic scale: the symmetric 'Egyptian' mode (red dots, Chinese ruibin diao^ⓘ guqin tuning) and the archaic 'blues minor' mode (blue dots, Chinese mangong diao^ⓘ tuning). Another instance of the close relation between golden ratio ⁠ $\varphi$ ⁠ and the number $5$ .

Notes

^ $({\tfrac {1}{2}})^{2}+1^{2}={\tfrac {5}{2^{2}}}$

References

^ Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. p. 11. ISBN 9-781-61614-424-1.
^ Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York City: Broadway Books. p. 85. ISBN 0-7679-0816-3.
^ Olsen, Scott (2006). The Golden Section: Nature's Greatest Secret. Glastonbury: Wooden Books. p. 3. ISBN 978-1-904263-47-0.
^ Van Mersbergen, Audrey M., Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic, Communication Quarterly, Vol. 46, 1998 ("a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")
^ Livio, Mario (2014). "The Golden Ratio in Art: Drawing heavily from The Golden Ratio" (PDF). p. 6. Retrieved 2019-09-11.
^ Livio 2003, p. 136.
^ Le Corbusier, The Modulor, p. 35, as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture (1999), p. 320. Taylor & Francis. ISBN 0-419-22780-6: "Both the paintings and the architectural designs make use of the golden section".
^ Joyce, David E. (2014). "Euclid's Elements, Book XIII, Proposition 10". Department of Mathematics, Clark University. Retrieved 2024-09-13.
^ Burger, Edward B.; Starbird, Michael P. (2005). The Heart of Mathematics: An Invitation to Effective Thinking. Springer. p. 382. ISBN 978-1931914413.
^ Analogue to the construction in: Crilly, Tony (1994). "A supergolden rectangle". The Mathematical Gazette. 78 (483): 320–325. doi:10.2307/3620208.

External links

Weisstein, Eric W. "Golden Rectangle". MathWorld.
Weisstein, Eric W. "Golden Ratio". MathWorld.
The Golden Mean and the Physics of Aesthetics
Golden rectangle demonstration With interactive animation
From golden rectangle to golden quadrilaterals Explores some different possible golden quadrilaterals

[1] $({\tfrac {1}{2}})^{2}+1^{2}={\tfrac {5}{2^{2}}}$

[2] Posamentier, Alfred S.; Lehmann, Ingmar (2011). The Glorious Golden Ratio. Prometheus Books. p. 11. ISBN 9-781-61614-424-1.

[Livio-3] Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, The World's Most Astonishing Number. New York City: Broadway Books. p. 85. ISBN 0-7679-0816-3.

[4] Olsen, Scott (2006). The Golden Section: Nature's Greatest Secret. Glastonbury: Wooden Books. p. 3. ISBN 978-1-904263-47-0.

[5] Van Mersbergen, Audrey M., Rhetorical Prototypes in Architecture: Measuring the Acropolis with a Philosophical Polemic, Communication Quarterly, Vol. 46, 1998 ("a 'Golden Rectangle' has a ratio of the length of its sides equal to 1:1.61803+. The Parthenon is of these dimensions.")

[6] Livio, Mario (2014). "The Golden Ratio in Art: Drawing heavily from The Golden Ratio" (PDF). p. 6. Retrieved 2019-09-11.

[FOOTNOTELivio2003[httpsarchiveorgdetailsgoldenratio00maripage136_p._136]-7] Livio 2003, p. 136.

[8] Le Corbusier, The Modulor, p. 35, as cited in Padovan, Richard, Proportion: Science, Philosophy, Architecture (1999), p. 320. Taylor & Francis. ISBN 0-419-22780-6: "Both the paintings and the architectural designs make use of the golden section".

[9] Joyce, David E. (2014). "Euclid's Elements, Book XIII, Proposition 10". Department of Mathematics, Clark University. Retrieved 2024-09-13.

[10] Burger, Edward B.; Starbird, Michael P. (2005). The Heart of Mathematics: An Invitation to Effective Thinking. Springer. p. 382. ISBN 978-1931914413.

[11] Analogue to the construction in: Crilly, Tony (1994). "A supergolden rectangle". The Mathematical Gazette. 78 (483): 320–325. doi:10.2307/3620208.

[a]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]